整体观下的单元首课教学

摘 要：所谓“单元整体”，就是通过“整”（整合、梳理）将单元内容融合成“体”（体系、结构）。从首课的角度看，“整”的路径主要有：按数学研究的基本规范提出、解决大问题；按数学知识的逻辑结构扩展迁移已有体系。“空间基本图形位置关系”单元的“体”是立体几何的公理体系，可以采用后一种“整”的路径。其首课《平面的基本性质》应该通过类比，从点、直线的概念到平面的概念，从平面几何中点、直线的基本性质到立体几何中平面的基本性质，最后展望整个单元的研究内容。

关键词：高中数学；单元教学；整体观；首课；《平面的基本性质》

作为一种新的教学观，单元整体教学已经成为当前数学教学的趋势和方向。而数学课是一节一节地上的，内容也是一节一节地呈现的。如何让学生认识到分散地学习的内容之间具有联系，基于整体的观念进行若干节课的学习，是单元整体教学的关键问题。笔者认为，每个单元的第一节课（单元首课）应该为整个单元的内容播下种子，从而定下具有整体结构的生长基因。

最近，我们设计并由顾秋婷老师执教了《平面的基本性质》一课（“空间基本图形位置关系”单元首课，也是立体几何理论体系单元首课），得到了听课老师们的好评。课后，我们对备课过程、课堂教学进行了回顾、反思。我们觉得，这节课比较成功的主要原因就是基于单元整体教学的理念，合理设计单元首课的教学，让单元“整体”之树有了生长之根。下面结合这节课谈谈我们在这方面的思考。

一、 关于单元整体教学的思考

（一） “体”是目标，“整”为路径

通常情况下，“整体”是一个词，不能分开理解，如《现代汉语词典（第7版）》将其解释为“一个由有内在联系的部分所组成的体系”。因此，“单元整体教学”就是要揭示单元各部分内容的“内在联系”，将单元内容组成一个体系。由此，我们认为，“整体”的关键是“体”（体系），“体”是一种结构、一个系统，数学教学（特别是单元整体教学）应该以“体”为目标。

如果将“整体”仅作为一个名词，那么，“单元整体教学”中的“整体”就只是针对目标而言的一种要求。我们认为，“单元整体教学”中的“整体”不仅是目标要求，而且有路径指引。事实上，“整体”一词中的“整”有整合、凝聚、条理化、系统化的意思，是将部分“整”为有联系的体系的意思。因此，“整”就是实现整体教学的一种路径，没有“整”就形不成“体”。

由此，我们认为，所谓“单元整体”就是通过“整”将单元内容融合成“体”。这里的“整”指整合、梳理，即通过整合的方式对单元内容、学科思想等进行梳理；这里的“体”指体系、结构，就是使单元内容达成融合，即在某种形式上构成一个系统，形成数学知识结构（内容）或数学研究范式（过程）。

那么，如何“整”呢？教学中有很多路径，如用逻辑链接、用思维连贯、用思想贯穿、用观念统整、用文化融合、用结构架构等。

（二） 始于首课，贯穿始终

因为“整”的对象是整个单元的内容，所以从表面上看，应该在单元的所有内容都学习后再进行，但是，这种认识是错误的，是与单元整体教学的理念背道而驰的。单元整体教学的本质是用大观念（大概念）来整合（梳理）单元的内容，而这种观念（概念）是起引领作用的，是自始至终的，所以“整”的过程应该贯穿单元教学的全过程。那么，从“始于首课”的角度看，主要有哪些“整”的路径？

一般而言，数学内容的陈述有两种方法。一种是以发现、提出问题和分析、解决问题的过程所产生的知识前后关系进行陈述。因为按数学研究的基本规范展开单元内容的学习，单元内容学习的先后次序就构成了本单元的“体”（一种具有线性关系的、体现问题解决思维过程的“体”）。另一种是对研究之后得到的所有相关知识以逻辑关系进行陈述。［1］这是按数学理念体系的框架而建构的“体”（在数学公理化思想下建构的“体”）。中学数学教材中，这两种陈述形式兼而有之，甚至经常混合使用。这是从数学研究过程或数学研究方法的角度分类的。从整体教学的角度看，它们都是路径之一，但又都需要进行改造。

前一种路径是面对真实情境（大背景），发现和提出问题，也就是承载了单元核心思想（大观念）的大问题，再按数学研究的基本规范，在解决大问题的过程中形成本单元的知识结构。在这种路径下，单元首课要面对大背景，提出大问题，揭示其本质；在后续的学习过程中解决大问题，形成问题链，建构知识体系。

后一种路径是根据单元内容的数学本质与核心思想（即数学研究之后的知识整理），提出数学内部的结构性问题（即已有数学知识理论基础上的扩展性问题），运用数学知识的逻辑结构（如公理化体系）整合单元内容。在这种路径下，单元首课要将学生已有的数学知识整理出逻辑结构，从而提出扩展性问题，运用思维迁移，特别是类比的方式，对新学习的单元内容进行结构化建构，形成新知识的整体构架。

二、 整体观下《平面的基本性质》一课的教学思考

（一） 目标导向，合理定位

对于具体的单元内容而言，究竟如何选择整合的路径？这与单元内容的特点、价值以及学生的认知基础密切相关，也就是需要由单元学习之后应该达到的目标定位而定。

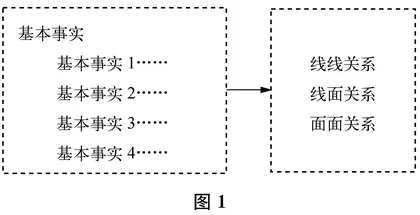
“空间基本图形的位置关系”单元的教学内容是立体几何的理论体系，该单元的知识结构是以欧几里得希尔伯特公理体系为基础的数学逻辑结构（如图1所示）。由此可以明确：本单元的“体”应该是立体几何的公理体系（考虑到学生的认知能力，不完整呈现整个体系）。

立体几何的相关知识在学习之初还没有产生，因此，本单元首课的教学不同于对已有知识整合、梳理，而只能按照数学逻辑结构的基本范式进行知识探索与体系建构，即采用上文所述的“后一种路径”。

数学知识整理的典型工具是公理化方法，这是将研究成果组织为数学理论的使用最为广泛的方法。因为数学理论的组织是基于演绎推理的，在数学理论中，每一个命题都应该能从一些较为基本的命题纯逻辑地推导出来；基于同样的道理，那些较为基本的命题也都应该能从更为基本的命题纯逻辑地推导出来；这样一直追溯过去，在这个理论的开头，就得把一个或一组命题当作最基本的事实，不加证明地接受下来，这便有了公理。［1］也就是说，本单元首课应该从选择公理开始。

（二） 基于“基因”，定向“生长”

从一节课中看出单元整体轮廓，至少看出单元整体走向，并且对单元内容的学习与研究有引领作用，这是单元整体教学中单元首课的重要任务。单元的整体轮廓或整体走向应该由单元的生长基因决定，单元的生长基因就应该蕴含在单元首课的背景性资料中。

“后一种路径”的背景性资料就是“数学内部的结构性问题”。因为学生已经具有了平面几何的学习经验，而平面几何学习已经有机渗透了公理化的思想方法，用平面几何作为种子进行类比教学，立体几何就有了生长的基因：通过类比，由平面几何的基本事实发现立体几何的基本事实，由平面几何的知识结构建构立体几何的知识结构。这样，单元首课就为整个单元的知识内容、结构体系以及学习过程做好了铺垫。平面几何的知识结构从基本事实开始，正好对应“空间基本图形位置关系”单元首课的教学内容，即“平面的基本性质”。于是，本单元的生长基因就确定了：从直线的概念到平面的概念，从平面几何中的基本事实到立体几何中的基本事实，由基因的正常生长，立体几何的大树（知识结构）就自然地长成了。

三、 整体观下《平面的基本性质》一课的教学设计

（一） 引入课题

谈话：上一单元，我们认识了很多空间图形，这些图形都是由点、直线或面（包括平面、曲面）组成的。在初中平面几何中我们已经研究了点、直线及由它们所构成的图形，那么，我们如何研究空间中的基本图形点、直线和平面呢？

谈话引出课题，并为后面学生类比平面几何研究立体几何做出铺垫。

（二） 生成平面的概念

学生对平面并不陌生，因为小学、初中认识的很多几何体中的“表面”都给学生以平面的印象。尽管如此，“平面”这个概念并不简单，在几何知识体系中它是一个不加定义的“元概念”，其数学“生成”方式可以为本单元的整体教学提供“整”的路径示范：

问题1：初中学习“平行线”概念时是用“同一平面内没有公共点的两条直线”来定义的，这里提到平面。多面体的表面是“面”，它是平面的一部分。那么，什么是平面呢？平面如何生成呢？

引导学生回顾平面几何中点概念、直线概念的形成方式和基本特性，类比建构平面概念的形成方式和基本特性，得到表1。

（三） 建构平面的基本性质

问题2：如何刻画平面的基本性质呢？

引导学生回顾平面几何中如何刻画点、直线的基本性质，得到表2。

追问：平面几何中，是用点与线、线与线的相互关系刻画点、直线的基本性质的，其中的“相互关系”就是初中教材中的“基本事实”或其推论。也就是说，可以用相互关系的基本事实来刻画几何对象的基本特性。那么，如何用相互关系的基本事实来刻画平面的基本性质呢？

引导学生类比发现立体几何中，可以用点与面、线与面和面与面的相互关系来刻画平面的基本性质，从而列出表3。

在此基础上，首先引导学生回顾平面几何中点与直线相互关系的结论“两点确定一条直线”，类比得到立体几何中点与平面相互关系的结论，即公理1：不在同一条直线上的三点确定一个平面。其中，“不在同一条直线上”这个条件要在学生思考后加上去。然后，画图表示。

其次引导学生回顾平面几何中直线与直线重合的结论“若直线a上有不同的两点在直线b上，则直线a、b重合”，类比得到立体几何中直线在平面上结论，即公理2：若一条直线上有两点在一个平面上，则这条直线上所有的点都在这个平面上，这时称这条直线在这个平面上。然后，画图表示。

再次引导学生回顾平面几何中直线与直线相交的结论“两条相交直线有且只有一个公共点”，类比得到立体几何中平面与平面相交的结论，即公理3：若两个平面有一个公共点，则它们有无数个公共点，这些点在同一条直线上。然后，画图表示。

最后引导学生研究公理1的三个推论。

这里需要说明的是，平面几何中直线与直线平行的结论“过直线外一点有且只有一条直线与已知直线平行”对应的立体几何中的结论（公理）留到下节课处理。

问题3：上面已经用自然语言、图形语言表述了三个公理及公理1的推论，那么怎样用符号语言来表述它们呢？

由学生考察上述命题，发现就是要用符号表示出点在直线上、点在平面上、直线在平面上、直线与直线相交、直线与平面相交、平面与平面相交等关系。

追问：根据直线、平面的形成方式，直线、平面都可以看作点的集合，那么你觉得这些关系可以用怎样的符号来表示呢？

由学生想到用集合的符号语言来表述，并用表格将自然语言与符号语言对应起来。最后让学生用符号语言分别表述三个公理及公理1的推论。

（四） 运用与拓展

通过几个例子展示平面基本性质的运用，如用公理及其推论说明生活现象的原理、用公理证共面问题等。然后，出示图2，介绍立体几何公理化的进程［2］。

（五） 展望后续研究内容

问题4：平面几何中在“基本事实”后研究了哪些内容？立体几何中应研究哪些内容？

由学生给出：直线与直线、直线与平面、平面与平面的位置关系，特别是平行与垂直两种特殊的位置关系；点与线、点与面、线与线、线与面、面与面在各种位置关系下的度量关系。最后形成结构化板书（如图3所示）。

本节课从平面的概念到平面的基本性质，始终运用与平面几何类比的方式，展开研究过程，详细展现公理体系的建构过程；最后再用展望的方式，构建本单元知识结构图，为单元教学提供基本路线。

参考文献：

［1］ 赵慈庚.初等数学研究［M］.北京：北京师范大学出版社，1990：122123.

［2］ 袁小明.数学思想史导论［M］.南宁：广西教育出版社，1991：7279.