苏科版初中数学新教材活动资源的评价之用

摘 要：充分利用苏科版初中数学新教材中的学习活动资源，可以有效开展诊断性、形成性、表现性、终结性四大学习评价，实现以评促教、以评促学，优化教学的过程。具体地，可以着眼“章首活动”，考查已有学习基础；聚焦“问题”和“活动”，考查知识发生过程；关注“数学探究”，考查学生个性特征；透视练习系统，考查核心素养表现。

关键词：初中数学；新教材；学习活动；学习评价

以学生为主体的数学教学是“数学活动”的教学。它要利用一些可能的资源、手段让学生参与到数学活动中，而不只是简单地“听老师讲”——虽然认真听讲也是学习数学的重要方式。由此，教师就能更好地观察到学生的学习表现，并对学生的学习状况进行评价，从而“以学定教”，即以“反馈—矫正”的方式促进学生进一步学习。这样，在教学目标的统领下，就能很好地实现“教、学、评的一体化”。依据《义务教育数学课程标准（2022年版）》修编的苏科版初中数学教材（以下简称“新教材”）很好地体现了这一理念。使用新教材时，教师要充分利用其中的学习活动资源，开展多元的学习评价。

一、着眼“章首活动”，考查已有学习基础

“章首活动”是新教材的一个特色板块，它是在每章开始处设计的具有趣味性、操作性和思考性的数学活动。一方面，通过“章首活动”，可以引导学生从已有知识和生活经验出发，在“做数学”中走向本章知识及其蕴含的思想方法。另一方面，“章首活动”可以成为诊断学情的载体，有效考查学生学习本章内容的已有学习基础，帮助教师在诊断性评价的基础上，更好地确定教学的起点和进程。

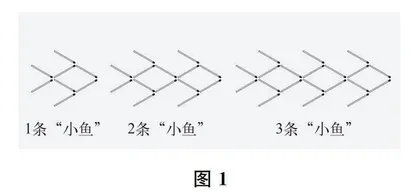
例如，七年级上册第3章《代数式》的“章首活动”：

按下页图1的方式，用火柴棒搭“小鱼”。

1. 搭1条、2条、3条“小鱼”各用多少根火柴棒？

2. 按同样方式，搭20条“小鱼”要用多少根火柴棒？

3. 如果用n表示所搭“小鱼”的条数，那么搭n条这样的“小鱼”需要多少根火柴棒？

学生在完成这个“章首活动”的过程中，需达到两个层面的要求：一是在操作的基础上直接数出火柴棒的根数；二是在操作、数数的基础上找出规律，并用字母描述这个规律。因此，学生完成活动的情况能诊断不同的学习基础，可以为后续教学定调定节奏。

又如，七年级下册第10章《二元一次方程组》的“章首活动”：

在学习一元一次方程时，我们曾列一元一次方程解决了“鸡兔同笼”问题（如图2）。

1. 填写表1，你可以发现哪些等量关系？

表1 “鸡兔同笼”问题中的有关数量

2. 你能列出几个关于x、y的方程？你能根据所列方程求出x、y的值吗？

这个“章首活动”既是学习本章内容的开始，也能唤醒学生对一元一次方程学习内容的回顾，继而引导学生类比一元一次方程的学习经验，依据其中的研究路径，探索解决问题的方案。教师可以通过对学生解决有关问题的诊断性评价，确定后续教学的难易快慢：如学生已有解决有关一元一次方程问题的良好基础，则无须反复呈现一元一次方程的有关内容，只要略加提及即可。

二、聚焦“问题”和“活动”，考查知识发生过程

“问题”和“活动”是新教材的节首栏目，设计的是有关数学概念、公式、定理、法则等具有数学思维价值的问题，其目的是引导学生通过观察、猜想、实验、分析、思考、探索等活动，获取数学知识和方法，积累学习经验。“问题”和“活动”栏目能助力教师有效开展形成性评价，考查数学知识的发生过程。同时根据评价结果可以调整学习进程，即时发现问题，及时反馈矫正。

例如，七年级上册第2章第5节第1小节《有理数的乘法》节首的“问题”：

如图3，在水文观测中，常常关注水位的高低与升降。如果水位每天下降4 cm，那么如何计算3天后的水位变化？

使用这一问题情境后，教师可以接着提出问题：

如果规定水位上升为正，下降为负，请用一个等式表示水位变化。

在学生得到（-4）×3=-12后，教师可以继续提出问题：

你能用相反数的意义来说明（-4）×3=-12吗？

如何计算4×（-3），（-4）×（-3）？

这里，围绕教材中的“问题”素材设计相关问题链，使得教学过程成为学生自主探究、合作交流的过程。这一过程中，教师通过对学生的形成性评价来反馈调节教学进程，通过启发引导、适时介入、铺垫提示来促进学生自主建构有理数乘法法则。

又如，七年级下册第9章第2节第1小节《轴对称的概念》节首的“活动”：

1. 在一张纸上滴一滴墨汁，将纸对折、压平，然后重新展开，你有什么发现？

2. 将一张透明纸对折，在折痕的一边画一个三角形，在折痕的另一边描出这个三角形，展开透明纸，你有什么发现？

教学中，通过学生操作活动，教师引导学生得出轴对称、对称轴等概念后，可以提出如下问题：

请你画出成轴对称的两个三角形，说出对称轴、对称点、对称线段。

说说成轴对称的两个图形有哪些特点？

这里，从两个活动到轴对称概念是一个从具象感知到数学化表达的过程，而两个问题的回答是学生对上述过程理解的显化呈现，因此，教师对学生这一过程中表现的形成性评价，是决定教学难易快慢的依据：如学生理解有困难，则需要增加直观感知的内容，以确保教学目标的实现。

三、关注“数学探究”，考查学生个性特征

“数学探究”是新教材的又一个特色板块，它在每章结尾处，需要学生运用本章所学的知识和方法解决一个具有一定挑战性的问题，强调学科知识的综合，带有显著的操作性、实践性特点。与“综合与实践”一样，“数学探究”教学中对学生学习的评价应突出表现性评价，以学生在活动中的自主性、操作性、实践性、创造性为评价的主要内容，考查学生的个性特征。

例如，七年级上册第2章《有理数》章尾的“数学探究”——“算‘24’”内容：

我们约定一副扑克牌中的J为11，Q为12，K为13，A为1，黑色数字为正数，红色数字为负数。例如，图4中两张扑克牌分别表示9、-11。

将一副扑克牌（除去“大王”“小王”后）平均分给2（或4）人，每人每次出2（或1）张牌，将牌面所表示的数进行有理数的加、减、乘、除、乘方运算（每张牌只能用1次）。先算得“24”者记2分，然后将这4张牌放一边；若无人算得“24”，则把这4张牌放一边，但不计分。如此继续下去，直到大家不能出牌为止。积分多者为胜。

请你和同学算“24”。

“算‘24’”作为与有理数运算相匹配的游戏操作类“数学探究”，适标性强，趣味性强，突出了算理算法，具有较好的数学思维价值。教学中，教师宜对学生的探究情况进行质性评价，也就是突出表现性评价，可以关注“活动过程”与“学习效果”两个维度：“活动过程”评价可以包括“活动完成情况”“合作交流情况”“数学思考、解决问题的情况”等；“学习效果”评价可以包括“参与数学活动的积极性、主动性”“过程中问答、发言的情况”“获得发展的情况”等。

又如，八年级下册第7章《认识概率》章尾的“数学探究”——“摸球试验”也是如此。其内容如下：

在一只不透明的袋子中装入白球和红球共10个，这些球除颜色外都相同。从中任意摸出1个球，记录颜色后将球放回袋子中并摇匀。

（1）每人摸球30次，把结果填入下页表2。

（2）汇总小组每位同学试验结果，估计“摸到白球”与“摸到红球”概率。

（3）根据试验结果，猜一猜袋子中的白球和红球各有几个？

（4）打开袋子，验证一下：你的猜想正确吗？

（5）在生活中，常会听到有人说对某件事的判断“十拿九稳”。你能用随机事件的概率解释这种现象吗？你自己是否也有过“十拿九稳”的感觉？

四、透视练习系统，考查核心素养表现

新教材的练习系统包括每课时的练习、每节的习题与每章的复习题。它具有“精炼实用”（精准性）、“情境新颖”（时代性）、“思维价值”（生长性和探究性）的特点，有助于学生形成知识结构、领悟思想方法，因而，突出了核心素养导向，是终结性评价的重要载体。用好这一练习系统，是开展学生学习终结性评价的基础，也是提高课堂教学质量的重要保证。

例如，七年级上册第4章《一元一次方程》的一道复习题：

有研究认为，14—17周岁男性每天约需要摄入75 g蛋白质。某天小明哥哥刚好通过面粉和牛肉共600 g实现了75 g蛋白质的摄入量，已知每100 g面粉约含蛋白质10 g，每100 g牛肉约含蛋白质20 g，这天他摄入面粉和牛肉各多少克？

八年级上册第4章第1节《平面直角坐标系》的一道习题：

图5是某次越野跑赛道图，小明根据该赛道图绘制了一个平面直角坐标系。在这个平面直角坐标系中，站点A和站点B的坐标分别是（4，0.4）、（-3.2，1.1），补给站C恰好位于坐标原点，请在图中画出补给站C的位置。

这两道习题都基于真实情境，具有时代性的特点，能有效评估学生运用数学知识分析问题、解决问题的能力。

此外，针对学生某些特定素养的培养，新教材还提供了系统的训练素材，可以用于评价。

例如，七年级下册第12章《定义 命题 证明》的一道复习题：

已知：正整数n能被3整除，也能被7整除。求证：n能被21整除。

八年级下册第9章《因式分解》的一道复习题：

已知m＞0，且m是奇数。求证：m²-1能被8整除。

九年级上册第1章《一元二次方程》的一道复习题：

求证：对于任意的实数k，关于x的方程（x-1）（x-2）＝k²有两个不相等的实数根。

上述复习题需要学生通过形式化的手段，利用代数命题推理的基本方法进行有别于运算的代数演绎推理。这些也是评价学生推理能力的有效素材。

综上，充分利用新教材中的学习活动资源，可以有效开展诊断性、形成性、表现性、终结性“四大”学习评价，实现以评促教、以评促学，优化教学的过程。