数学教学中创新意识的培养*

摘要：创新意识是义务教育阶段数学学科核心素养的主要表现之一。它的内涵包括三个维度：尝试发现与提出问题；通过归纳与类比的方式猜想、发现；探索非常规的开放性问题。数学教学中，可以采取鼓励质疑问难、引导发散思维、组织综合实践等途径或策略培养学生的创新意识。

关键词：创新意识；数学核心素养；问题提出；合情推理；开放问题

本文系江苏省南京市教育科学“十四五”规划课题“指向育人：‘开放性数学问题’驱动下初中生创新意识培养的实践研究”（编号：L/2024/048）、江苏省中小学教学研究第十五期重点课题“实践育人：指向素养发展的初中数学跨学科项目教学的研究”（编号：2023JY15ZA10）的阶段性研究成果。

一、 创新意识的内涵

《义务教育数学课程标准（2022年版）》（以下简称“新课标”）将创新意识作为小学与初中阶段数学核心素养的主要表现之一，

并指出：“创新意识主要是指主动尝试从日常生活、自然现象或科学情境中发现和提出有意义的数学问题。初步学会通过具体的实例，运用归纳和类比发现数学关系与规律，提出数学命题与猜想，并加以验证；勇于探索一些开放性的、非常规的实际问题与数学问题。”［1］

可见，创新意识的内涵包括三个维度：

一是尝试发现与提出问题，也可以说是“问题意识”。爱因斯坦说过：“提出一个问题往往比解决一个问题更为重要，提出新问题需要创造性的想象力，而且标志着科学的真正进步。”［2］蔡金法教授也指出：数学课标强调发现与提出问题，所要实现的两个重要改变之一就是学生的创新意识。［3］例如，从生活现象中提出问题：车轮为什么都是圆形的？身份证号码中有哪些信息？人为什么会打呵欠？

……从自然现象中提出问题：彩虹为什么总是弯曲的？星星为什么会闪？向日葵为什么总是朝着太阳？……从数学现象中提出问题：1×1＝1，11×11＝121，111×111＝12321，那么，111111111×111111111的结果符合类似的规律吗？11n的结果有什么规律？……

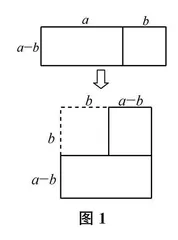
二是通过归纳与类比的方式猜想、发现，即合情推理（探索性思维）。国内外，通过G.波利亚和徐利治等学者的著作，人们已经认识到：数学研究（学习）不仅需要演绎推理和确定性思维，而且需要合情推理和探索性思维——后者包含更多的创造性成分。例如，计算15×15、25×25、35×35等的结果后猜想一般性结论，就是一种归纳推理；由平方差公式的图形推导方法（如图1所示）得到完全平方公式的推导方法（如图2所示）和立方差公式的推导方法（如图3所示），则是一种类比推理。它们都具有探索中的创造性。

三是探索非常规的开放性问题，也可以说是探索性问题（exploratory problem）、结构不良问题（ill-structure problem）、调查性项目（investigative project）、现实主义数学（realistic mathematics）等［4］。开放题在近几十年全世界的数学教育领域备受瞩目，其原因主要在于：弥补了一般性练习（重视内容知识的掌握）所缺乏的为数学过程思维（尤其是高层次思维，如创造性思维）的发展提供的自由空间（课程载体），促进了数学教育中至为重要的内容（知识）与过程（思维）的平衡。［5］例如：在等边三角形ABC所在的平面内找一点E，使得△EAB、△EAC、△EBC都是等腰三角形，这样的点E有多少个？这样的条件或结论不唯一、不确定的开放性问题，能引导学生多角度探索，培养学生的创新意识。

二、 创新意识的培养

针对创新意识内涵的三个维度，数学教学中，可以采取鼓励质疑问难、引导发散思维、组织综合实践等途径或策略培养学生的创新意识。下面重点结合初中数学教学的具体案例加以说明。

（一） 鼓励质疑问难

创新意识表现为尝试发现与提出问题。因此，教师要多鼓励、引导学生提出问题，尤其是提出自己在学习中感到疑难困惑的问题。为此，要创设宽松自由的教学氛围，让学生敢于质疑问难；还要适当地设计情境和引导语［6］，让学生能够质疑问难。

【案例1】“负负得正”是如何得来的？

教学“有理数的乘法”时，“负负得正”的解释始终是绕不过去的难关。苏科版初中数学教材这样解释：水位一天下降4 cm，三天下降12 cm，所以（－4）×3＝－12；（－4）×3与（－4）×（－3）互为相反数，所以（－4）×（－3）＝12。这样的解释将实际背景与代数推理相结合，使得大部分学生相信这一法则成立。但是，还有学生不能理解：为什么两个负号相乘，就变成了正号？负号去哪里了？教师要允许、鼓励学生表达这样的困惑，然后顺着学生的思路循循善诱：（－1）×（1－1）等于多少？［（－1）×（1－1）=（-1）×0=0。］假设（－1）×（－1）＝－1，那么（－1）×1＋（－1）×（－1）等于多少？（－1－1＝－2。）乘法分配律还成立吗？［因为（－1）×（1－1）≠（－1）×1＋（－1）×（－1），所以乘法分配律不成立了。］由此，通过逆向思考让学生认识到：“负负得正”是一种规定，不能证明，但很合理——能使乘法分配律依然成立。

【案例2】“边边角”能否判定三角形全等？

学完“三角形全等的判定”后，学生回顾已有的判定条件，很容易发现它们都是三组边或角对应相等且至少有一组是边，从而对为什么没有“边边角”这样的条件感到困惑。果然，一次教学中，一名学生问道：为什么“边边角”不可以判定两个三角形全等？我画的就可以！教师肯定了他善于思考、敢于提问，然后追问：能告诉我你画的具体边长和角度分别是多少吗？该生答道：两条边长分别是2 cm和3 cm，其中2 cm所对的角是30°。教师便让其他学生也按该生设定的数据画出三角形，然后组织全班交流，引导学生发现：可以画出两种三角形（如图4所示），同一种三角形能够完全重合，即全等；不同种三角形不能完全重合，即不全等，且有一组内角互补。然后，教师继续追问：那么，“边边角”条件是一定不可以判定两个三角形全等，还是有时不可以（有时可以）判定两个三角形全等？学生进一步探索，发现：当条件角是直角或钝角且对着条件边中的大边时，可以判定两个（直角或钝角）三角形全等（这其实推广了“HL”判定方法）；当两个条件边相等且条件角为锐角时，也可以判定两个（等腰）三角形全等。这样，通过质疑问难，学生对“三角形全等的判定”有了新的认识。

【案例3】任意的四边形都有内切圆吗？

学完“三角形的内切圆”后，教师引导学生回顾相关知识：三角形都有外接圆和内切圆；当且仅当对角互补（对角之和相等）时，四边形有外接圆。然后让学生提出问题。学生自然地提出了：四边形有内切圆吗？什么时候四边形有内切圆？这个问题有一定的难度。教师引导学生从特殊情况出发，画图探索。学生先发现：正方形、菱形、筝形有内切圆，一般的矩形、平行四边形没有内切圆。便猜想：当邻边相等时，四边形有内切圆。教师引导学生进一步思考：反过来成立吗？当邻边不相等时，四边形可能有内切圆吗？学生想到梯形还没有研究，于是继续画图探索，发现：特殊梯形（如等腰梯形、直角梯形）和一般梯形都可能有内切圆，也可能没有内切圆。教师引导学生根据内切圆与四条边都相切，首先由与两底所在直线（两条平行线）相切作出可能的内切圆，然后构造梯形，让两腰也与所作圆相切（如图5所示）。然后让学生思考：在两腰变化的过程中，梯形的边或角之间是否存在不变的数量关系？由此，学生能够发现：梯形的对边之和始终相等。

进而，运用切线长定理，便可证明：当且仅当对边之和相等时，四边形有内切圆。

（二） 引导发散思考

创新意识又表现为归纳、类比，从而猜想、发现。相对于演绎推理，合情推理是一种探索性思维，具有很强的不确定性，或者说发散性。因此，教师要多鼓励、引导学生发散思考、举一反三，使学生打开思维的大门，从不同的角度展开思考，尤其要使学生不满足于既有认识与想法，不断拓宽视野，探索新的理解与思路。为此，在知识教学中，要引导学生转换表征形式，联想相关知识，使学生在发散思考中，完善CPFS结构［7］；以此为基础，在解题教学中，要使学生在发散思考中，从“一题多解”走向“一题优解”［8］。

【案例4】数字“1”有多少种表达形式？

在一节复习课上，教师提问：对于数字“1”，你能想到几种表达形式？在教师的引导下，学生发散思考，得到：（1） 分数及百分数的形式，如1＝22＝100%；（2） 和的形式，如1＝12＋12＝0.5＋0.5；（3） 积的形式，即互为倒数的两个数之积；（4） 幂的形式，如1＝12014＝20；（5） 三角函数的形式，如1＝sin2α＋cos2α＝tan 45°……

【案例5】由等式x2＋y2＝1能想到什么？

在一节复习课上，教师提问：由x2＋y2＝1，你能想到什么？经过5—8分钟的思考，学生想到：（1） x=0、y=1等取值情况；（2） 斜边长是1的直角三角形三边的数量关系；（3） sin2α＋cos2α＝1；（4） 平面直角坐标系中，以原点为圆心、1为半径的圆上点的坐标满足的关系式；（5） 完全平方公式（x＋y）2＝1＋2xy、（x-y）2＝1-2xy。这里，（1）是将等式看作一个二元方程，找到多组解；（2）（3）（4）是把数量关系图形化（代数问题几何化），变成“形”结构——初中数学课程中，对三角函数的理解偏向几何；（5）是对“数”结构的拓展，即由平方和的结构想到和（差）的结构、积的结构。

在此基础上，教师继续提问：x＋y有最大值吗？是多少？很快，就有学生按照刚刚的理解给出了解决的思路：（1） 根据“数”结构，设x＋y＝t，得（t－y）2 ＋y2＝1，将其看作关于y的一元二次方程，整理成一般形式得2y2－2ty＋t2－1=0，由该方程有解，即判别式大于等于0，易得t的取值范围。（2） 根据“形”结构，作出图6，设AB=x，AC=y，BC=1，则点A在以BC为直径的半圆上，设点D在BA的延长线上，AD=AC，则BD=x＋y，易得∠BDC=45°，因此点D在以BC为弦的优弧上，所以，BD为该优弧所在圆的直径时，x＋y最大。这样，就以发散思考为基础，从知识理解走向了问题解决。

（三） 组织综合实践

创新意识还表现为探索非常规的开放性问题。从课程内容的角度看，“数与代数”“图形与几何”“统计与概率”等知识领域的问题多为指向具体知识巩固应用的封闭性（结构良好）问题，不是真正意义上（“问题解决”中）的问题；“综合与实践”这个非知识领域的问题基本上是开放性（结构不良）问题，才是真正意义上（“问题解决”中）的问题。广义上，“综合与实践”问题是“真实情境”下的问题，基于数学现实，包括数学内部问题和数学外部问题，强调综合性或实践性，因而，更不确定，更需要探索，更能凸显学生个性。因此，教师要多设置“综合与实践”问题，多组织综合实践活动。

【案例6】将正方形分割成等腰直角三角形

教学“轴对称图形”一章后，可以出示人教版初中数学教材配套的教师用书提供的问题：

你能将正方形割成6个等腰直角三角形吗？如图7，已经给出了一些画法，你能继续完成一些吗？

本题具有很强的开放性：条件很简单，结论却非常丰富多样。参考已经给出的样例，经由教师的引导，学生能够发现：连对角线可以得到一些等腰直角三角形；作斜边上的高可以将已有的等腰直角三角形分割为两个等腰直角三角形；作与对角线平行的线可以在一个角落分割出等腰直角三角形，并与所平行的对角线夹一个等腰梯形；适当调整与对角线平行的线，可以让所夹的等腰梯形能分割为若干个等腰直角三角形……然后不断尝试，可以得到多种不同的分割方法。

【案例7】绘制学校平面图

教学“图形的测量与性质”“图形的位置与坐标”的相关知识后，教师参考新课标附录1的例60，提出问题：你能将美丽的校园绘制到图纸上，利用平面图形的形状、大小以及位置关系表明校园中的各个场所和区域吗？然后引导学生将其分解为若干个子问题：会用到哪些数学工具？（比例尺、方向的判定、图形形状的判定、图形大小的测量以及图形位置关系的判定与测量等。）校园内都有什么场所？场所之间是什么区域？它们都有什么作用？行政楼、教学楼、体育馆、操场、景观、道路等场所或区域是什么形状的？有关的长度、角度等怎么测量？（利用正规的测量工具或因地制宜地采用标准物、“身体尺”等工具；多次测量取平均值）立体的校园如何呈现在平面的图纸上？……

经过讨论，初步解决这些问题后，还要组织学生分工完成测量和绘制。比如：有小组测量建筑场馆（可以数地砖）；有小组测量开放区域（可以数步数、“手拉手”数人数）；有小组搜集资料，汇总数据；还有小组转换数据，按照适当的比例尺绘图，等等。此外，还要组织学生交流（相互评价）实践成果，反思测量、绘制过程，总结经验教训。

【案例8】新能源汽车真的普及了吗？

教学“统计与概率”的有关知识后，教师与学生谈论时下的热点话题——新能源汽车。出示新闻：“根据网络数据显示，2024年上半年新能源汽车的总销量已累计达到389万辆，比去年增长32.5%。”然后提问：这样的数据在本地是否有可信度？可以采取怎样的手段证实或证伪这一点？经过课堂讨论，教师组织学生课外分工展开调查：（1） 对比分析网上各地新能源汽车的比例；（2） 在多个小区停车场数绿牌车和蓝牌车的数量；（3） 在某个交通要道早、中、晚三个时间段分别统计10分钟以内绿牌车和蓝牌车的数量。（4） 设计调查问卷，统计汽车出行人员的车辆信息。获得数据后，组织学生在课堂上选择合适的统计图表整理数据，进行分析，作出判断，同时比较不同调查方式所得结果的异同，感悟数据的随机性和规律性。

参考文献：

［1］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022：11.

［2］ 爱因斯坦，英费尔德.物理学的进化［M］.周肇威，译.长沙：湖南教育出版社，1999：59.

［3］［6］ 蔡金法，王涛.体现和落实核心素养：解读新课标中的“问题提出”［J］.教育研究与评论，2022（10）：412.

［4］［5］ 孙旭花.数学问题设计的误区和出路［J］.教育研究与评论，2023（3）：5156.

［7］ 傅赢芳，喻平.CPFS结构理论及其对数学概念教学的启示［J］.教育研究与评论（中学教育教学），2020（6）：2833.

［8］ 顾锋，宁连华.数学解题教学：从“一题多解”到“一题优解”［J］.教育研究与评论（中学教育教学），2023（7）：712.