“拓展创新学程”几何与代数主题编写特色及教学建议

摘要：《普通高中拓展创新学程·数学》中的几何与代数主题共设计了24个专题，体现了“三见三更见”的编写特色：见树木更见森林；见方向更见路径；见“人材”更见人才。对此，提出三点教学建议：精研“两高一标”，发挥学程效益；锤炼基本方法，提高实践能力；注重数学探究，提升创新能力。

关键词：高中数学；拓展创新学程；几何与代数

高中数学课程中，几何与代数主题内容丰富，“在必修课程与选择性必修课程中，突出几何直观与代数运算之间的融合，即通过形与数的结合，感悟数学知识之间的关联，加强对数学整体性的理解”［1］，是培养学生直观想象、逻辑推理、数学抽象、数学建模、数学运算等核心素养的重要载体。

本文简单介绍《普通高中拓展创新学程·数学》（以下简称《拓展创新学程》）中几何与代数主题的基本内容，重点阐述其编写特色和教学建议。

一、 基本内容

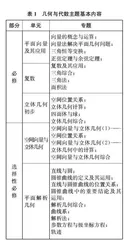
《拓展创新学程》中的几何与代数主题突出高中数学课程中有关的核心知识与重要方法，在苏教版高中数学教材编写的基础上延伸、拓展，共设计了24个专题（见下页表1），为学生提供思维进阶、能力提升的材料。

这样的专题设置充分接轨新高考，突出新高考中的重点考查内容，如：立体几何部分的设置，突出了空间角与空间距离的计算，与球有关的切、接、截问题等；解析几何部分的设置，突出了圆锥曲线中的定点、定值等热点问题。另外，几何与代数主题下还设置了方法专题，如向量法、三角法、面积法、解析法等，进一步突破了章节的局限，引领学生跳出知识的框架，用方法串通，增进学生的数学理

二、 编写特色

《拓展创新学程》中几何与代数主题内容的编写，力求挖掘教材中有关知识与方法的背景、本质、联系，体现“三见三更见”。而且，每道例题后面都设置了引领性的栏目，或是“思考”，或是“回顾”，或是“拓展”，引领学生进一步探究、反思、完善，促使学生提升数学思维、掌握解题方法，拓展数学知识、完善认知结构。

（一） 见树木更见森林

1. 延伸知识

著名数学教育家G.波利亚说过：“拿一个有意义又不复杂的题目去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的领域。”将教材中的知识由此及彼、由特殊到一般地延伸、推广，使学生不仅能看见一棵棵树木，更得见广阔的森林，从而养成反思的学习习惯，培养自主探究的能力，发展数学思维。

比如，第22讲“正弦定理与余弦定理”例2：

已知△ABC的三个内角A、B、C的对边分别为a、b、c，s＝12（a＋b＋c）。求证：△ABC的面积为S△ABC＝s（s－a）（s－b）（s－c）。（秦九韶海伦公式）

教材中给出了用两边和夹角表示的三角形面积公式S△ABC＝12absin C，本题又给出了用三边求三角形面积的方法。推陈出新，只需使用余弦定理与同角三角函数关系，就可以化角为边sin C＝1－cos2 C＝1－a2＋b2－c22ab2，进而证明秦九韶海伦公式。本题后的“拓展”则继续给出了圆内接四边形用边长表示的面积公式，带学生领略秦九韶海伦公式的一般性，并为数学拔尖的学生开启进一步探索的大门：圆内接n边形的面积是否都能用边来表示？非圆内接的n边形（即没有外接圆的n边形）的面积呢？

2. 强化联系

教材中的知识是分章节编排的，这从形式上割裂了（或者说没有充分展现）知识之间的丰富联系。加强知识之间的联系，如用函数的观点看待数列、用向量表现复数的运算、用三角处理复数的乘法等，引导学生感悟树木之间的互相扶持，有利于学生的整体理解。

比如，第23讲“复数及其应用”例2：

求最小的正整数n，使得I＝12＋123in为纯虚数，并求出I。

复数的n次幂运算往往蕴含着一定的“周期性”。运用复数的三角形式，并结合棣莫弗定理，将其转化成关于辐角的三角函数，易于发现复数的n次幂运算的变化规律。本题旨在引导学生体会复数三角形式的优势，感悟复数的n次幂与三角函数的联系，促进学生的整体理解。

3. 拓展方法

高考试题的创新激发解题方法的创新。这要求学生不能固守一种方法，而要根据具体条件进行创新求解。《拓展创新学程》中几何与代数主题内容的编写，力求展现一类常考问题的“妙手”解法，使学生会一法而通一片，助力学生提高解题效益。

比如，第51讲“曲线系”例7：

在平面直角坐标系xOy中，已知点F1（-17，0）、F2（17，0），点M满足MF1－MF2＝2，记点M的轨迹为C。

（1） 求C的方程；

（2） 设点T在直线x＝12上，过点T的两条直线分别交C于A、B两点和P、Q两点，且TA·TB＝TP·TQ，求直线AB的斜率与直线PQ的斜率之和。

本题第（2）问考查直线与双曲线相交的有关内容，解决方法较多，对解析几何的运算要求高。如果从平面几何的角度看，TA·TB＝TP·TQ所描述的恰是相交弦定理，可知A、B、P、Q四点共圆。因此，可利用经过A、B、P、Q四点的曲线系方程解决。曲线系方程避开了直线与二次曲线的联立过程，可以大大减轻计算量，使问题迎刃而解。

4. 揭示本质

试题的命制往往隐藏本源，取其特殊状态，从而常出常新。《拓展创新学程》中几何与代数主题内容的编写，力求对问题追根究底，揭示本质，以帮助学生透视“枝繁叶茂”下的“发达根系”，深化认知，从而“心知肚明”地解题。

比如，第40讲“圆锥曲线中的重要结论及其运用”例8：

如图1，已知A、B分别为椭圆E：x29＋y2＝1的左、右顶点，P为直线x＝6上的一个动点，PA与椭圆E的另一交点为C，PB与椭圆E的另一交点为D。求证：直线CD过定点。

本题考查动直线过定点的证明，常规方法是联立直线PA与椭圆E的方程，解得交点C的坐标，再同样求出点D的坐标，继而证明直线CD过定点即可。这体现出解析几何的一般特点：好想难算。充分分析条件，转换思路，简化运算是本题优化解决的追求。如可以利用直线PA与PB的斜率之间的比例关系简化运算。像这种“动点P所在的定直线”与“动直线CD所过的定点”相互辉映的考题很多，本题后的“拓展”便揭示了这类问题的本质——极点和极线，给出了圆锥曲线极点对应的极线方程，引领学生站在一定的高度看问题。

（二） 见方向更见路径

1. 普适，让方向显而易见

《拓展创新学程》中几何与代数主题内容的编写，并不一味追求奇思妙想，而更注重通性通法，将普适的方法梳理出来，如解析法、三角法、向量法等，引导学生认识每种方法的适用范围，为学生指明解题的方向，照亮解题之路。

比如，第37讲“直线与圆”例6：

如图2，设H是锐角三角形ABC的垂心，由点A向以BC为直径的圆作切线AP、AQ，切点分别为P、Q。求证：P、H、Q三点共线。

正如著名数学史家M.克莱因所说，解析几何彻底改变了数学的研究方法。解析法是解决平面几何问题的一把利器。本题是一道与圆有关的平面几何问题，要证明P、H、Q三点共线，只需证明垂心H在切点弦PQ所在的直线上；建立平面直角坐标系，用解析法即可解决，使思考（特别是寻找辅助线）的难度大大降低。本题后的“思考”将半圆改为半椭圆，提出同样的问题，引导学生继续探究，感悟圆与圆锥曲线的统一性。

又如，第35讲“三角法”例4：

设正数x、y、z满足x＋y＋z＝xyz，求证：11＋x2＋11＋y2＋11＋z2≤32。

观察发现：条件等式与三角形中的三角恒等式tan A＋tan B＋tan C＝tan Atan B·tan C的结构一致，而所证式子中的根号又可通过1＋tan2 x＝1cos2 x去掉，因此本题适用三角法解决。本题后的“回顾”进一步给出了三角形中的常见三角恒等式。［2］熟记这些结论，当代数式出现类似结构时，就可以构造三角形进行三角代换，化复杂为简单。

2. 转化，让路径更加清晰

数学问题的解决常要经历化难为易、化繁为简的转化过程，如求线段长度时的斜化横（纵），空间线线、线面、面面之间平行与垂直关系的互相转化，空间问题的平面化处理等。明晰转化的方向，形成具体的做法，能让学生的解题路径更加清晰。

比如，第25讲“空间位置关系”例3：

在棱长为1的正方体ABCDEFGH中，M、N分别是棱CG、AE的中点，P为侧面BFGC上一点，并且满足EP∥平面BMN，求EP长度的取值范围。

空间中的平行和垂直问题往往通过平行转化关系“线线平行线面平行面面平行”和垂直转化关系“线线垂直线面垂直面面垂直”来处理。本题中，动直线EP过定点E，要平行于平面BMN，则必在平面BMN的平行平面内，因此可转化为面面平行问题，点P的轨迹就是该平行平面与侧面BFGC的交线。

3. 优化，让路径更加通畅

拔尖创新人才的培养不能拘泥于已有方法，而要锤炼思维，不断优化，从而让思路更加简洁顺畅。《拓展创新学程》中几何与代数主题内容的编写，通过挖掘题目的解法，或展现优化的过程，或展现优越的方法，帮助学生创新解题视角，提升思维品质。

比如，第39讲“直线与圆锥曲线的位置关系”例3：

如下页图3，过抛物线y2＝2px（p＞0）外一点P向抛物线作两条切线，切点分别为M、N，设F为抛物线的焦点。

（1） 求证：PF2＝MF·NF；

（2） 求证：∠PMF＝∠FPN。

对偶运算在解析几何中较为常见，如用－k替换k，用－1k替换k等。本题中，PM与PN是过同一点所作的抛物线的切线，因此，M、N两点的地位相同，只需用点N的横、纵坐标x2、y2分别替换切线PM的方程中的x1、y1，就可以直接得到切线PN的方程。本题后的“回顾”进一步揭示了圆锥曲线的整体性：如果椭圆中有某个结论，那么，只需以－b2替换椭圆结论中的b2，就得到了双曲线中对应的结论。

（三） 见“人材”更见人才

1. 关注思维灵活性

数学教育既要培养基础扎实的“人材”，更要培养思维灵活的人才。《拓展创新学程》中几何与代数主题内容的编写，注重从不同角度解决问题，引导学生养成多角度分析问题的习惯，增强思维的灵活性。

比如，第19讲“向量的概念与运算”例1：

已知单位向量a、b满足a·b＝0，若向量c＝7a＋2b，〈a，c〉表示向量a、c的夹角，则sin〈a，c〉＝（）

A. 73B. 23C. 79D. 29

向量具有数与形的双重属性。本题属于常规题，最容易想到的是利用向量的数量积求cos〈a，c〉，为此需要先求c的模或坐标。而从形的角度，构造矩形，作出7a、2b与c，则在直角三角形中，很容易求得sin〈a，c〉的值。迅速选择从形的角度解题，能够体现学生对向量的深刻理解以及思维的灵活性。

2. 激发思维创造性

创新人才的培养离不开创造性思维的锤炼。创新人才在遇到问题时，应当能多角度、多方面、多层次、多结构地思考和探寻答案。《拓展创新学程》中几何与代数主题内容的编写，努力通过问题的设置，引导学生经历观察、分析、综合、归纳、类比、抽象、概括等思维过程，创造性地解决问题。

比如，第25讲“空间位置关系”例7：

有三个给定的经过原点的平面，过原点作第四个平面α，使之与给定的三个平面形成的三个二面角均相等，这样的平面α的个数是。

过同一点的三个平面相交的情况较为复杂。从相交产生的交线来看，它们或交于同一条直线，或交于三条不同的直线，可分两种情况处理。本题涉及的平面较多，先考虑两个平面成二面角的情况，得出一般结论，再考虑增加平面的个数，就比较容易处理了。这一退一进之间彰显着创新的意识和创造的能力。本题可被看成是从“平面中与两条相交直线所成角相等且过交点的直线有几条”类比而来的。从平面到空间的类比，可以产生很多新颖而有趣的问题。