基于差错分析的初中概率计算题教学

摘要：初中概率计算题主要是古典概型计算题，并且不需要通过计数原理计算，只需要列举统计一次随机试验及某个随机事件包含的等可能结果数。学生解题困难的根源在于，不能针对随机试验的基本过程或要素进行分析，正确得到（表示出）所有等可能出现的结果。对此，教学要重体验，让学生感受等可能出现的结果源自随机试验的过程（要素）;重表达，让学生学会不重不漏地列举出所有等可能出现的结果。

关键词：概率计算;古典概型;学生错误;等可能;树状图

概率计算是数学中考的重要考点之一，题目难度适中，但学生在解题中频频出错。本文结合几道学生错误率较高的概率计算题，分析差错原因，梳理教学对策。

一、初中概率计算题的典型差错分析

初中概率计算题主要是古典概型计算题，并且不需要（其实是不能够，因为没有学习过）通过计数原理计算，只需要列举统计一次随机试验及某个随机事件包含的等可能结果数。因此，学生解题困难的根源在于，不能针对随机试验的基本过程或要素进行分析，正确得到（表示出）所有等可能出现的结果。因而，学生解题的错误集中表现在，凭感觉或从其他主观臆断的角度分析，得到一些并不等可能出现的结果，并据此进行计算。

最简单的例子是，同时抛掷两枚相同的硬币一次，有学生认为，朝上的一面等可能出现的结果有“两正”“一正一反”“两反”三个。实际上，这三个结果不是等可能出现的。正确的解法是，两枚硬币整体朝上一面的结果是两枚硬币各自朝上一面的结果组合决定的，因此等可能出现的结果有“A正B正”“A正B反”“A反B正”“A反B反”四个。

下面来看两个复杂一点的例子：

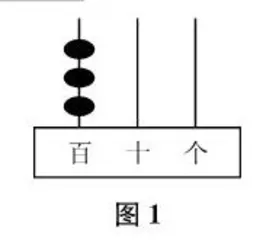
题1把3颗算珠放在计数器的3根插棒上构成一个数字，例如图1摆放的算珠表示300。现将3颗算珠任意摆放在这3根插棒上。若构成的数是两位数，则十位数字为1的概率为。

学生的错误解答是：构成两位数一共有12、21、30三个等可能出现的结果，其中十位数字为1的有1个，所以概率是13。这里出错的原因是，学生得到的结果不是等可能出现的。正确的解法是，3颗算珠整体摆放的结果是3颗算珠各自摆放的结果组合决定的，因此可以逐个写出3颗算珠摆放的结果，形成一个整体的结果，从而一一列举出所有等可能出现的结果：（十，十，十）、（十，十，个）、（十，个，十）、（十，个，个）、（个，十，十）、（个，十，个）、（个，个，十）。因此，一共有7个等可能出现的结果，其中十位数字为1的有3个，所以概率为37。

题2某初中每天对全校学生的午休情况进行检查，初一、初二、初三3个年级都要被检查到。某天由甲、乙、丙3名同学检查，他们来自3个不同的年级，每人只能检查1个年级。求他们都不检查自己所在年级的概率。

学生的错误解答是：他们要么检查自己所在的年级，要么不检查自己所在的年级，所以概率是12。这里出错的原因同样是，学生得到的结果不是等可能出现的。正确的解法是，3名同学整体检查的结果是3名同学各自检查的结果组合决定的，因此可以基于题目条件的限制，一一列举出所有等可能出现的结果：（初一，初二，初三）、（初一，初三，初二）、（初二，初一，初三）、（初二，初三，初一）、（初三，初一，初二）、（初三，初二，初一）。再假设3名同学分别来自初一、初二、初三（其他情况下结果数不变），从而找出他们都不检查自己所在年级的结果：（初二，初三，初一）、（初三，初一，初二）。最终求出概率为26=13。

此外，还有一类错误可以归结为审题不清（或缺少生活常识），没有注意到题目（或生活实际）已经对随机试验可能出现的结果做了限制，即有些结果理论上可能发生，实际上不可能发生。例如：

题3小秋打算去某影城看电影。她用手机打开购票页面，发现座位已售和可选情况如图2所示（虚线框内为黄金区域，其余为普通区域;深色为已售座位，白色为可选座位）。

（1）小秋独自观影，她选择第4排或第5排的概率是;

（2）小秋约小叶一同观影，求她选择的2个同排相邻的座位恰好都在黄金区域的概率。

解本题时，有学生没有注意到深色为已售座位，不能选择，不能作为一次试验的结果，因而出现错误。

二、基于差错分析的教学建议

（一）重体验，让学生感受等可能出现的结果源自随机试验的过程（要素）

概率计算都是随机试验（事件）引发的，随机试验有一定的现实性与操作性。因此，教师不能让学生只凭借想象和思考，抽象地理解随机试验，计算有关概率，而要充分设计实践活动，让学生亲自做随机试验，体验试验的基本过程及要素，从而真正地感受到等可能出现的结果源自随机试验的过程（要素），学会分析概率计算题中等可能出现的结果，认识概率的本质。

比如，设计这样一道题：2封信投到3个不同的信箱，共有多少种等可能的结果？课前准备2个信封a、b，3个盒子A、B、C，让学生拿着2个信封去投。学生在操作过程中，会先拿其中一个信封去投，再拿另外一个信封去投，从而能体会到一次试验是投2封信到3个信箱，2封信都投完，试验才完成。虽然初中没有教学分步计数原理，但是，可以通过这个试验让学生感受到分步完成。由此，试验结果就是2封信分别在哪个信箱，列出来应该是（A，A）、（A，B）、（A，C）、（B，A）、（B，B）、（B，C）、（C，A）、（C，B）、（C，C）这9种，它们是等可能出现的。此外，还要引导学生注意到，如果不加区分，（A，A）和（B，B）、（A，B）和（B，A）等有可能被看成同一个结果，而这样得到的结果就可能不是等可能出现的，因此，一定要抓住随机试验的基本过程或要素，分析所有等可能出现的结果。

（二）重表达，让学生学会不重不漏地列举出所有等可能出现的结果

有时，随机试验的基本过程比较复杂（要素较多），包含的等可能出现的结果较多。因此，学生即使知道抓住随机试验的基本过程或要素进行分析，也很难不重不漏地列举出所有等可能出现的结果。对此，教师既要引导学生抓住随机试验的基本过程或要素逐个有序地思考，也要引导学生借助列表、树状图等方法清楚地表达出结果。一般地，若随机试验的基本过程包括两个步骤（要素），可以用列表或树状图的方法;若随机试验的基本过程包括三个及以上步骤（要素），最好用树状图的方法。

比如，上述试题1中的随机试验就包括三个步骤（要素），可以用树状图的方法表达出在没有“构成的数是两位数”的条件限制下（实际上，此题有第2问，即求构成的数是三位数的概率，就去掉了“构成的数是两位数”的条件限制）所有等可能出现的结果（如图3所示）。