初中数学“孪生题”设计

摘要：作为一种比较简单的分层作业及一题多变形式，“孪生题”是指针对相同的核心知识与主要方法设计的情境背景一致、呈现形式类似，而能力要求（难度）有较明显差异的两道题。初中数学教学或评价中，可以设计表象与实质互补的“孪生题”，考查基础知识的理解;设计条件或结论变化的“孪生题”，考查推理、计算能力。

关键词：初中数学;“孪生题”;分层作业;一题多变

所谓“孪生题”，是指针对相同的核心知识与主要方法设计的情境背景一致、呈现形式类似，而能力要求（难度）有较明显差异的两道题（我们将其中较容易的题称为A类题，较困难的题称为B类题）。这是一种比较简单的分层作业及一题多变形式。背景、形式的相似可以凸显可选性（让学生觉得只选择一道题不会错过知识的巩固或方法的训练），能力要求（难度）的不同则体现了分层性（适应不同学生的需要），并且具有互补或相助的功能。

本文结合具体案例，谈谈初中数学“孪生题”设计的基本思路。

一、表象与实质互补的“孪生题”，考查基础知识的理解

设计考查概念、性质理解的“孪生题”时，A类题可以“回忆”的方式呈现，考查概念、性质的表象;B类题可以“不同表达”或“应用求解”的方式呈现，考查概念、性质的实质。这样的一组题层次分明，具有互补的功能：学生既可以选择其中的一道题，完成相应的能力目标，又可以同时完成两道题，实现对同一知识完整认识的目的。

题1（A类）解不等式-2x≤6得x≥-3，依据是_____________________________________。

（B类）“不等式的两边都乘（或除以）同一个负数，不等号的方向改变。”用字母表示这条性质：_____________________________________。

题2（A类）甲、乙两名射击运动员在某场测试中各射击20次，经过计算，他们的平均成绩相同。若要比较这两名射击运动员的成绩哪一个更为稳定，通常需要比较他们成绩的（）

A. 众数B. 平均数

C. 中位数D. 方差

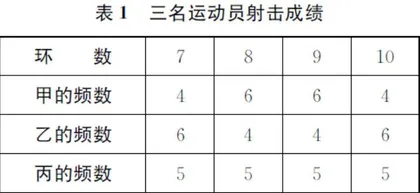
（B类）甲、乙、丙三名射击运动员在某场测试中各射击20次，他们的成绩如表1所示。

则甲、乙、丙三名运动员成绩最稳定的是（）

A. 甲 B. 乙 C. 丙 D. 三人相同

这里，题1和题2的A类题分别要求回忆“不等式的性质2” 的内容和“方差”的作用;题1的B类题要求用符号语言表达“不等式的性质2”（这种表达形式课本上没有呈现），是一种符号意识的升华要求;题2的B类题要求运用“方差”刻画“稳定”的含义，既可以计算求解，也可以将“表”抽象成“图”，从形的角度得到答案。

二、条件或结论变化的“孪生题”，考查推理、计算能力

传统的数学三大能力是推理能力、计算能力和空间想象力，所以，常见的有一定综合性的数学题主要基于相关知识，通过推理、计算及数形结合解决。虽然这样的数学题可能存在“掐头去尾烧中段”的问题，但因为三大能力的重要性，依然是数学教学及其评价中重要的题目类型。

设计主要考查推理、计算能力的“孪生题”时，基本的思路是对已知条件或所求（证）结果（结论）做局部变化，以改变题目难度（增减推理或计算的步骤）。这样的一组题也层次分明，并具有相助的功能：学生既可以选择其中的一道题，完成相应的能力目标，又可以通过较易题的解决为较难题的解决铺垫基础或提供思路。下面，分两种情况举例说明（例子相对集中于平面几何及其与函数图像综合的领域，因为这一领域的问题更能凸显对推理、计算能力的考查）。

（一）已知条件一样，所求（证）结果（结论）不同

题3（A类）如图1，将正方形纸片ABCD的一角折向边BC，使点A与BC上一点E重合，若BE=1，CE=2，则BF的长为_____________________________________。

（B类）如图1，将正方形纸片ABCD的一角折向边BC，使点A与BC上一点E重合，若BE=1，CE=2，则折痕FG的长为_____________________________________。

题3中，A类题所求的BF长只需要基于由折叠得到的EF=AF=AB-BF，在Rt△BEF中使用一次勾股定理即可求得;而B类题所求的FG长需要利用Rt△BEF∽Rt△CIE∽Rt△HIG（I为CG与EH的交点）求出CI和IG，再添加辅助线构造新的直角三角形求解。

题4（A类）如图2，BD、CE是△ABC的高，相交于点F，求证：△ABD∽△ACE。

（B类）如图2，BD、CE是△ABC的高，相交于点F，求证：△AED∽△ACB。

题4中，A类题的结论可以直接利用“两个角分别相等的两个三角形相似”证出;而B类题的结论需要利用△ABD∽△ACE得到AD∶AB=AE∶AC，再结合∠A=∠A证出。

（二）已知条件不同，所求（证）结果（结论）一样

题5（A类）如图3，正方形OABC的顶点A、C分别在x轴、y轴上，顶点B在反比例函数y=kx的图像上，已知点A的横坐标为1，则k的值是。

（B类）如图4，正方形OABC的顶点A、B都在反比例函数y=kx的图像上，已知点A的横坐标为1，则k的值是_______。

题5的A类题中，正方形OABC的顶点A、C分别在坐标轴上，点B在反比例函数的图像（双曲线）上，根据正方形的性质，由点A的坐标可以直接得到点C的坐标，进而得到点B的坐标，再将坐标代入表达式即可算出k的值;B类题将正方形OABC倾斜后，求k的值需要综合运用正方形（或等腰直角三角形）的性质、全等三角形的判定与性质、解一元二次方程等知识，经历较为复杂的推理、计算过程才能得到结果。

题6（A类）在某两个时刻，太阳光线与地面的夹角分别为37°和45°，树AB长6 m。如图5，若树与地面l的夹角为90°，求两次影长的和CD。

（B类）在某两个时刻，太阳光线与地面的夹角分别为37°和45°，树AB长6 m。如图6，若树与地面l的夹角为α，求两次影长的和CD。（用含α的式子表示）

题6的A类题中，AB⊥CD，可以分别通过一步计算得出CB、BD的长，再相加即可求解;B类题将AB倾斜后，需要经历构造直角三角形，在三个直角三角形中利用锐角三角函数求解的过程，还要用字母参与运算，计算量和计算难度都有所增加。

题7（A类）如图7，在菱形ABCD中，∠ABC=60°，以CD为边在菱形的外部作正三角形CDE，连接AE，求∠AEB的度数。

（B类）已知四边形ABCD是菱形，以CD为边在菱形的外部作正三角形CDE，连接AE、BE，求∠AEB的度数。

题7的A类题在给出图形，并且明确了菱形ABCD中的∠ABC=60°的情形下，图形识别容易，几何推理简单;B类题则不再呈现图形，而且删去了∠ABC=60°的条件（做了一般化推广），考查学生能否把文字“翻译”成图形，以及能否运用分类思想画图，进而运用基本量思想，借助等腰三角形顶角与底角的关系完成比较复杂的几何推理。