新课标“数与代数”内容分析：从结构到要求

摘要：《义务教育数学课程标准（2022年版）》对数与代数领域，主要通过整合主题、加强各学段联系的方式实现内容的结构化，突出不同阶段的核心内容；内容呈现采用“领域+学段”的设计思路，让每个主题都指向核心素养的培养，并且在“内容要求”的基础上增加“学业要求”与“教学提示”等表述形式，使课程标准更具有操作性与指导性；内容要求则依据“数与运算”“数量关系”“数与式”“方程与不等式”“函数”五个主题层层递进，注重整体性与阶段性，关注学生的认知发展规律，引入计数单位统一数的概念与运算，加强代数推理。

关键词：数学新课标；数与代数；课程内容；结构化

较长的一段时间内，算术是我国小学数学课程的主要内容，与其相应的代数是我国初中数学课程的重要内容。1902至1963年，我国将算术作为一门独立的课程设置在小学阶段。这一期间，我国小学数学课程内容以算术为主。1978年，我国将“小学算术教学大纲”改为“小学数学教学大纲”。自此，算术不是独立的课程了，而是小学数学课程的一个学习领域。同时，小学数学课程中逐步渗透代数的内容，如1978年的小学数学教学大纲中设置了“简易方程”，1992年的小学数学教学大纲中设置了“代数的初步知识”等。

21世纪新课程实验以来，“数与代数”成为我国义务教育（小学与初中）阶段数学课程的一个学习领域。2001年颁布的《全日制义务教育数学课程标准（实验稿）》单独设置了“数与代数”领域，2011年颁布的《义务教育数学课程标准（2011年版）》（以下简称“2011年版课标”）和2022年颁布的《义务教育数学课程标准（2022年版）》（以下简称“新课标”）也保持了这一做法。在前两版课标中，“数与代数”领域的内容逐步丰富和完善，但是，依然存在数的概念与运算内容不统一，对代数推理重视不够等问题。新课标对“数与代数”领域的内容做了结构化整合，进一步优化和完善了内容设置。本文从内容结构、内容呈现、内容要求三个方面对新课标中的“数与代数”内容做具体分析。

一、新课标“数与代数”内容结构分析

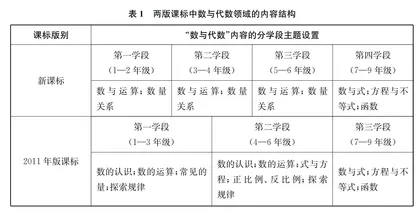
数学课程标准中，内容结构主要是指不同学段的课程内容所涵盖的知识领域及其主题的分布。与2011年版课标相比，新课标将原来的三个学段（小学为第一、第二学段，初中为第三学段）调整为四个学段（小学为第一、第二、第三学段，初中为第四学段）。同时，新课标对数与代数、图形与几何、统计与概率、综合与实践四个领域的课程内容进行了结构化整合。其中，对数与代数领域主要通过整合主题、加强各学段联系的方式实现内容的结构化，具体如表1所示。

与2011年版课标相比，新课标将小学部分的“数的认识”“数的运算”“常见的量”“探索规律”“式与方程”“正比例、反比例”六个主题整合成“数与运算”“数量关系”两个主题，初中部分的“数与式”“方程与不等式”“函数”三个主题保持不变。

将“数的认识”“数的运算”整合为“数与运算”，强调数与运算不可分离，体现了学科知识的整体功能和学生学习的整合优化。将“式与方程”“探索规律”“正比例、反比例”整合到“数量关系”中（其中，“方程”和“反比例”调整到初中阶段），突出了问题解决能力的培养。将“常见的量”调整到综合与实践领域，体现了跨学科主题学习的课程设计。

具体来看，数与代数的核心是运算，该领域的课程内容围绕运算对象、运算法则、运算应用等展开。小学阶段的运算对象主要是数，包括整数、分数、小数；初中阶段不仅将运算对象的范围扩展到有理数、实数，而且从数扩展到代数式。初中阶段的“数与式”是小学阶段的“数与运算”的延伸和扩展。

数学是研究数量关系和空间形式的科学，数量关系是数学和数学教育的核心主题。“数与运算”更侧重于数量的抽象和运算的法则，“数量关系”重点在于用数和符号表达现实情境中数量间的关系和规律，也就是用数学模型解决现实情境中的问题。小学阶段的“数量关系”主要指常量关系，包括常量之间的相等关系与比例关系。初中阶段的“数量关系”由常量关系扩展到变量关系，“方程与不等式”是刻画常量间的相等关系与不等关系的，“函数”是刻画变量间的关系的。初中阶段的“方程与不等式”“函数”是小学阶段“数量关系”的延伸和扩展。

综上可知，通过主题整合，突出了不同阶段的核心内容，使得数与代数领域的内容结构更具统整性，同时也加强了小学与初中内容间的衔接。

教育研究与评论中学教育教学/2022年11月热点透视二、新课标“数与代数”内容呈现分析

数学课程标准中，内容呈现主要是指课程内容的设计思路与表述形式。新课标中，“数与代数”内容的设计思路和表述形式有新的变化。

（一）“数与代数”内容设计思路分析

2011年版课标按照“学段+领域”的思路设计课程内容，数与代数领域的内容分散在三个学段中呈现。而新课标按照“部分+领域+学段”的思路设计课程内容，数与代数领域的内容按照小学、初中部分集中呈现，按照学段顺序一一展开。每个学段都有明确的主题（有的主题贯穿于不同学段），每个主题都指向核心素养的培养。比如，“数与运算”主题在第一学段主要指向数感、符号意识、运算能力的培养，在第二学段与第三学段增加了推理意识的培养，“数与式”主题在第四学段指向运算能力、抽象能力、推理能力的培养。通过在不同学段对同一主题不同内容的学习，可以促进学生核心素养的形成和发展。

（二）“数与代数”内容表述形式分析

与2011年版课标相比，新课标中课程内容的表述形式不仅有“内容要求”，而且增加了“学业要求”“教学提示”，即从“学什么”“学到什么程度”“怎样学”三个方面全面地表述课程内容。这加强了课程标准在教材编写、教学设计以及教学评价中的操作性与指导性。

例如，数与代数领域第一学段“数与运算”主题对“数”的具体内容要求是：“在实际情境中感悟并理解万以内数的意义，理解数位的含义，知道用算盘可以表示多位数。了解符号<、=、>的含义，会比较万以内数的大小；通过数的大小比较，感悟相等和不等关系。”这清晰地指出了第一学段“数”内容的学习范围。其学业要求是：“能用数表示物体的个数或事物的顺序，能认、读、写万以内的数；能说出不同数位上的数表示的数值；能用符号表示数的大小关系，形成初步的数感和符号意识。”这样的表述更加具体，不仅说明了“数”内容的学习程度，而且指明了通过“数”内容的学习应该获得的核心素养。而教学提示指出：“要充分考虑学生在幼儿园阶段形成的活动经验和生活经验，遵循本阶段学生的思维特点和认知规律，为学生提供有趣的活动，更好地完成从幼儿园阶段到小学阶段的学习过渡。”这样的教学提示在重视教师的教与学生的学的同时，也关注幼小衔接问题。

三、新课标“数与代数”内容要求分析

与2011年版课标相比，新课标数与代数领域的变化主要体现在，引入计数单位统一数的概念与运算，加强代数推理。以下具体分析该领域五个主题的内容要求。

（一）“数与运算”内容要求分析

“数与运算”主题贯穿于小学阶段的三个学段。与2011年版课标相比，新课标这一主题的变化主要是：增加了“探索加法和减法、乘法和除法的算理与算法”“探索并理解小数和分数的意义，感悟计数单位”的要求；将“负数”调整到综合与实践领域的主题活动“如何表达具有相反意义的量”中，把“百分数”调整到统计与概率领域，作为表达统计量的形式。集中体现在：通过引进“计数单位”，统一了数的概念与数的运算，加强了算理和算法。

计数单位对于认识数的本质和理解运算的本质具有重要作用，整数、小数、分数均可用“几个计数单位”表示，算理与算法也与计数单位紧密相关。过去，“数”的教学存在一个误区：对整数、小数、分数的认识各有各的教法，让学生误以为数的认识分三种形式，这影响了学生对数的意义的理解；尤其是小数的教学，让许多学生只会从现实世界的层面认识小数的意义，未能真正从数学的层面理解小数。新课标认为，整数、小数分别是以10n和10－n（n=0，1，2，…）为计数单位，分数是以1/n（n=1，2，…）为计数单位对数量多少的表达。这样可使学生从数的本质上理解整数、小数、分数的一致性。同样地，加法运算实际上就是计数单位的“累加”，而加法又是其他运算的基础，因而可以用计数单位解释运算。

新课标在“课程性质”中提到：“数学源于对现实世界的抽象，通过对数量和数量关系、图形和图形关系的抽象，得到数学的研究对象及其关系；基于抽象结构，通过对研究对象的符号运算、形式推理、模型构建等，形成数学的结论和方法，帮助人们认识、理解和表达现实世界的本质、关系和规律。”可见，抽象结构是数学体系构建的基础，而抽象结构就是“研究对象+运算或关系”构成的整体。新课标“数与运算”主题不单纯呈现数的概念，而将数与运算整合起来，一并述说数的概念、运算、运算律等，充分体现了“研究对象+”的设计理念。这样的呈现将数的认识与数的运算的学习统一起来，因为数的运算最终是要追溯到数的意义，而数的意义本质上均与计数单位相关。此外，新课标强调算理，就是强调基于数位分解（数的计数单位累计本质），利用运算律进行数的运算，即横式运算，如123×12=123×（10+2）=123×10+123×2=1230+246=1476。这实际上就是基于“数+运算”结构进行的运算。

新课标“数与运算”主题的内容要求按照学段不断拓展、层层递进。数的认识从整数、分数、小数到有理数、实数；数的运算从加、减、乘、除单一的运算到四则混合运算，并且随着数的认识的拓展、递进，从整数运算到小数、分数运算，再到有理数、实数运算。具体来看，第一学段学习万以内的数，强调从具体情境中的数量过渡到抽象的数的过程，在数量多少的比较过程中理解数的大小关系，培养符号意识和数感，在四则运算的学习过程中形成初步的运算能力。第二学段学习万以上的数、小数及分数，强调重视第一学段整数学习的经验，在数与运算的学习过程中体验数的认识及数的运算的一致性。第三学段要求通过整数、小数、分数的运算，进一步感悟计数单位在运算中的作用，感悟运算的一致性；在理解数的意义的基础上，探索自然数的性质，如2、3、5的倍数的特征，了解公因数、公倍数、奇数、偶数、质数、合数等概念，培养数感、运算能力、推理意识等。

（二）“数量关系”内容要求分析

“数量关系”主题贯穿于小学阶段的三个学段。与2011年版课标相比，新课标这一主题的变化主要是：将“方程”“反比例”调整到初中阶段，增加了“能用字母表示运算律”“认识‘总量=分量+分量’（加法模型）”“能在真实情境中，合理利用等量的等量相等进行推理，形成初步的推理意识”“探索用字母表示事物的关系、性质和规律的方法，感悟用字母表示的一般性”的要求。

具体来说，“方程”与“反比例”的学习对小学生存在困难，故将其调整到初中阶段。但新课标并没有削弱小学阶段代数思维的培养，而是更加重视从算术到代数的过渡，具体的体现是提升了“用字母表示数”的要求。与“数”相比，“用字母表示数”更具优越性。用具体的“数”只能“一个一个”地解决问题，而“用字母表示数”可以“一类一类”地解决问题，如用字母表示运算律等，这里面蕴含模型思想。以往只是将字母表示数作为数的进一步抽象、更一般表达，而新课标将字母表示数设置在“数量关系”主题下，把字母表示数理解为事物之间关系的一般性表达，如加法模型和乘法模型，以及运算律、计算公式等都可以用字母表示。因此，用字母表示数量关系和规律也是形成初步的代数思维的载体。此外，新课标将“等量的等量相等”作为代数推理的一个基本事实。过去的课程内容设置比较重视几何推理的一些基本事实，使学生误认为代数学习不需要推理。事实上，代数推理在基础教育阶段的数学学习中的使用更为广泛。新课标增加代数推理的基本事实，旨在加强代数推理。

新课标“数量关系”主题的重点在于用数和符号对实际情境中数量之间的关系和规律进行表达，进而用数学模型解决问题。其第一学段的内容与“数与运算”主题紧密相关，要求“能在熟悉的生活情境中运用数和数的运算，合理表达简单的数量关系，解决简单的问题”。第二学段，随着“数与运算”内容的丰富与深入，对“数量关系”相关内容的要求提升为“能在简单的实际情境中，运用四则混合运算解决问题”。在此基础上，第二学段还设置了“等量的等量相等”这一基本事实和常见的三种数量关系等内容，旨在发展学生的推理意识、模型意识和应用意识。第三学段的内容开始为从“常量”向“变量”过渡做准备，主要包括用字母表示数量之间的关系、比和比例、正比例等。

（三）“数与式”内容要求分析

“数与式”主题设置在第四学段，是对小学阶段“数与运算”主题的延伸和扩展，由有理数、实数、代数式三部分组成。与2011年版课标相比，新课标这一主题的变化主要是，增加了“理解负数的意义”“了解代数推理”的要求。与小学阶段一样，新课标也在初中阶段加强了代数推理。