以数学思想串联知识体系

摘要：《直线与方程》章复习课应该引导学生串联知识体系，进而综合运用知识解决问题。具体的教学过程可以分为“导入：明确复习目的，提示复习方法”“聚焦研究对象：用方程表示直线”“聚焦对象性质：用方程（参数）刻画直线的位置关系、有关距离”“聚焦结论应用：用方程（参数）解决直线问题”“小结：揭示数学思想，确立知识体系”等环节。

关键词：高中数学；章复习课；《直线与方程》；抽象结构；数形结合

一、教前思考

高中数学知识有着比较严密的逻辑体系。这种逻辑体系对促进学生智力发展、培养学生理性思维和科学精神、帮助学生形成良好的数学素养都有着举足轻重的作用。然而，落实到具体的操作层面，经过课时分解的课堂教学往往存在联系性不够、整体性不强，即知识体系割裂的不足。为了弥补这个不足，教师需要引导学生通过单元（包括教材章节自然形成的单元和教师教学重新组织的单元）复习将所学知识串联起来，形成良好的知识体系，从更高的层面审视整个单元的内容。

串联知识体系需要一定的线索。这个线索可以是数学的思想方法或研究路径（广义地看，研究路径，如从特殊到一般，也可以看作思想方法）。仔细分析所含内容，可以发现，苏教版高中数学教材中的《直线与方程》一章是以抽象结构思想和数形结合思想为线索展开的。

首先，本章内容一直贯穿着数学学科的一般研究路径，即抽象结构思想，用《义务教育数学课程标准（2022年版）》“课程性质”中的话就是，“数学源于对现实世界的抽象，通过对数量和数量关系、图形和图形关系的抽象，得到数学的研究对象及其关系；基于抽象结构，通过对研究对象的符号运算、形式推理、模型构建等，形成数学的结论和方法，帮助人们认识、理解和表达现实世界的本质、关系和规律”；用史宁中教授的解释就是，“不仅要知道研究对象是什么，更重要的是知道研究对象的性质是什么、关系是什么、运算是如何展开的……教概念的同时，应当教它的性质、关系或运算……”。简单地说就是，明确了形式化（抽象）的研究对象后，就要研究它的性质、关系等，进而要研究有关结论的应用（解决问题）。具体来说，本章以直线这一基本的几何图形为研究对象，研究了与它有关的角（方向）、点、位置关系、距离等方面的性质，并且展示了有关结论的应用。

其次，本章内容始终体现了解析几何分支的基本思想方法，即引入平面直角坐标系之后，用坐标（有序实数对）表示点，用二元方程或一元函数式（两个变量的关系式）表示曲线（点的集合或轨迹），这是数形结合思想中“以数解形”的重要体现之一。具体来说，本章聚焦直线（特殊的曲线）这一研究对象后，用二元一次方程来表示，进而利用方程研究与直线有关的性质，解决相应的问题。

因此，本章的复习课应该以抽象结构思想和数形结合思想引导学生串联知识体系，进而综合运用知识解决问题，并从中感悟数学思想，提升思维能力，进而能够在数学思想（一种大概念、高观点）的驱动引领下自主学习（探索）更多新知。

二、教学设计

（一）导入：明确复习目的，提示复习方法

投影展示华罗庚先生的话：“读书的真功夫在于既能把薄的书读成厚的，又能把厚的书读成薄的。熟书生温，但把新东西讲进去了，就能找另一条线索把旧东西重新贯穿起来。”

旁白进行目标和方法引导：“章节复习课的任务在于对所学内容进行再认识、再建构，我们可以用一条线索把散落于各节的旧知像珍珠一样串起来。这样才能在‘爬过一座座小山头’后，‘站在山顶回望来路’时，真正产生‘会当凌绝顶，一览众山小’的感觉。而这条线索，通常就是数学学习的灵魂——思想方法。那么，《直线与方程》一章的复习，应该以什么数学思想来串联全章内容呢？请大家在复习的过程中仔细体会。”

由此，让学生明确本节复习课的任务不只是对知识的重温及运用，更重要的是发现知识联系，形成整体认识，同时对串联知识体系的数学思想产生模糊猜测和强烈好奇。

（二）聚焦研究对象：用方程表示直线

提问：“通过本章内容的学习，你对标题‘直线与方程’有怎样的认识？”引导学生体悟平面内的直线与二元一次方程之间的对应关系，明确研究对象（直线）和方法（方程）。

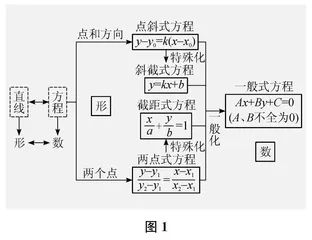
依次追问：“通常哪些要素可以确定一条直线？”“我们用斜率刻画方向，由点和斜率得到了点斜式方程，由两个点得到了两点式方程，那么直线方程还有哪几种形式？”“有人说‘直线方程的其他形式都是点斜式的推论’，对此你有什么看法？”引导学生从本源出发思考直线方程的由来以及不同方程形式之间的关系，在体会“以数解形”思想的同时，构建如下页图1所示的知识体系。

出示练习：写出下页图2中各直线的方程。让学生根据具体直线的几何特征选择合适的直线方程形式来表示，并重点巩固最重要的点斜式（l1）和两点式（l3），同时，关注斜率为0（l2）和斜率不存在（l4）这两种容易被忽略的特殊情况。

出示变式1：试写出一个方程，表示经过点（2，3）的所有直线。从特殊到一般，让学生写出过定点的直线系方程，从而更加深刻地认识直线方程的形式及参数与直线几何特征的关系。

出示变式2：m（m∈R）变化时，直线x－2y+m=0有怎样的几何特征？让学生逆向思考，根据含参数的直线方程分析出直线系平行的几何特征，即“以形助数”，从而充分地感受数形之间的互相转化。

（三）聚焦对象性质：用方程（参数）刻画直线的位置关系、有关距离

提问：“上述变式1和变式2涉及两条直线的相交关系和平行关系，那么，两条直线有哪些位置关系呢？怎么刻画（判定）呢？”引导学生继续“以数解形”，通过方程组解的情况或参数的几何意义得到参数的关系，刻画（判定）两条直线的各种位置关系，从而建构如图3所示的知识体系。

布置任务：“尝试类比‘直线的方程’‘两条直线的位置关系’，建构‘平面上的距离’有关的知识体系。”让学生继续自主“以数解形”，通过直线方程中的参数刻画（求解）与直线有关的距离，同时体会其中蕴含的化归转化思想，从而构建如图4所示的知识体系。图4（四）聚焦结论应用：用方程（参数）解决直线问题

出示以下例题及变式：

例题如图5，在矩形ABCD中，已知AB=3，AD=1，E、F为AB的两个三等分点，AC、DF相交于点G，证明：EG⊥DF。

变式1如图6，在矩形ABCD中，已知AB=3，AD=1，E、F为AB的两个三等分点，点T在边DC上，且点T到直线DF、AC的距离分别为d1、d2，求d1d2的最大值。

变式2如图7，在矩形ABCD中，已知AB=3，AD=1，E、F为AB的两个三等分点。若一质点从点E沿与BA夹角为θ的方向射到AD上的点M后，依次反射到DC、CB和AB上的点N、P、F（入射角等于反射角），则tan θ=，线段EM的长为。

变式3求x2+y2+x2+（y－1）2+（x－3）2+（y－1）2+（x－3）2+y2的最小值。

例题来源于教材（苏教版高中数学选择性必修第一册）第45页第17题，以学生熟悉的图形为载体，考查学生用两条直线垂直关系的方程（参数）刻画解决问题。变式1在例题图形的基础上增加了一个动点和两个点到直线的距离，思维量进一步提升，考查学生用点到直线距离的方程（参数）刻画及二次函数的性质解决问题。变式2继续以矩形和一边上的两个三等分点为载体，借助反射条件，考查学生多次用直线的点斜式方程（斜率通过入射角等于反射角获得）及直线交点的坐标解决问题——当然，本题也可由入射角等于反射角及三等分点条件，得到Rt△AME≌Rt△BPF，Rt△AME∽Rt△DMN，Rt△BPF∽Rt△CPN，Rt△DMN≌Rt△CPN来求解。变式3逆向设计，以代数式最小值的形式，考查任意一点到已知矩形四个顶点的距离和的最小值，让学生“以形助数”，再次充分地体会数形结合思想。

（五）小结：揭示数学思想，确立知识体系

引导学生从思想方法和知识体系的层面回顾本节课复习的过程，总结收获：基于抽象结构和数形结合思想，从研究对象到对象性质再到结论应用，从数到形并从形到数，形成了“直线与方程”一章的内容（知识及应用）体系。

最后，布置教材第45页第16、18、19题作为基础性作业，以及如下多选题作为拓展性作业，从而帮助学生深化复习内容，并拓展了解相关的数学史和数学文化。

1765年，瑞士数学家欧拉在其《三角形的几何学》一书中提出：任意三角形的外心、重心、垂心在同一条直线上。后人称这条直线为欧拉线。若已知△ABC的顶点A（-4，0），B（0，4），其欧拉线方程为x-y+2=0，则顶点C的坐标可以是（）

A. （2，0）B. （0，2）

C. （-2，0）D. （0，-2）