强化几何直观提升空间观念

［摘 要］尺规作图是小学几何教学中强化学生几何直观与空间认知能力、提高学生的逻辑推理能力与问题解决能力的重要手段。在小学阶段的尺规作图教学中，教师可以从以点带线、以线制角、以圆成方和以形表意四个方面形成多样化的教学策略，从而帮助学生理解抽象的几何概念，在实践中锻炼其逻辑推理能力、空间想象能力和数学应用意识，为其未来学习更复杂的几何知识奠定基础。

［关键词］几何直观；尺规作图；空间观念

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）05-0030-04

培养学生的空间观念和几何直观是小学数学教学的重要任务。尺规作图是一种传统而有效的几何教学方法，强调动手操作，直观性强，能够帮助学生理解抽象的几何概念，促进学生空间思维和逻辑推理能力的发展。因此，亟须进一步探索如何将尺规作图高效融入小学几何教学中。

一、尺规作图在小学几何教学中的应用价值

（一）培养学生的空间思维与几何直观

尺规作图是小学数学几何教学的重要内容之一，在培养学生的空间思维与几何直观方面扮演着关键角色。《义务教育数学课程标准（2022年版）》多处提及空间观念和几何直观，尺规作图正是培养学生空间观念和几何直观的有效途径。一方面，尺规作图有助于培养学生的空间思维。空间思维的形成直接影响着学生对空间和图形的理解与掌握水平。通过尺规作图，学生能够在动手操作中增强对几何图形和空间关系的感知，从而逐步形成清晰的空间思维。通过动手实践，学生能在构建图形的过程中不断进行空间想象和逻辑推理，有效促进空间思维能力的发展。尺规作图能够帮助学生理解几何概念，并使其在反复操作中逐步掌握抽象的空间关系，进而为后续更为复杂的几何学习打下坚实基础。另一方面，尺规作图对培养学生的几何直观具有重要意义。几何直观主要是指运用图表描述和分析问题的意识与习惯。该能力可帮助学生在数学学习中更好地理解几何问题，从而提高其解决问题的能力。通过尺规作图，学生能够将抽象的几何概念转化为直观的图形，从而极大程度提高对几何概念的理解水平。此外，尺规作图有助于学生在实践中发现和总结几何规律，从而进一步增强几何直观能力。

（二）培养学生的逻辑推理能力与问题解决能力

培养学生的逻辑推理能力与问题解决能力是小学数学教育的重要目标。尺规作图中，落在纸面上的作图轨迹对应着演绎推理的思路和步骤，可有效发展学生的推理意识，具体表现在三个方面。第一，尺规作图的每一步操作都基于明确的几何定理和公理，要求学生在作图过程中进行严密的推理和判断，从而逐步增强其演绎推理能力。基于逻辑推理的思维训练可有效促进学生在数学学习中形成严谨的思维方式，为今后的数学学习奠定坚实的基础。第二，尺规作图在培养学生问题解决能力方面具有显著优势。小学数学教育要培养学生在复杂问题情境中分析和解决问题的能力，而尺规作图中的几何问题推理、策略选择和结果验证等环节，能全面提高学生的问题解决能力和数学知识应用能力，从而提升学生的综合素养。第三，尺规作图在增强学生逻辑思维的系统性与严谨性方面也发挥着重要作用。学生在作图过程中需遵守几何规则，精准操作，保证推理的连贯性与严密性，从而在思考过程中保持严密的逻辑性，进而提升逻辑推理能力和问题解决能力。由此可见，尺规作图契合培养学生逻辑推理能力与问题解决能力的教育需求，是实现该教学目标的重要手段。

二、尺规作图教学的设计思路与实践应用

（一）以点带线，培养学生逻辑思维能力

在小学数学教学中，尺规作图不仅仅是一种几何构建工具，更是培养学生逻辑推理能力的有效手段。通过使用无刻度的直尺和圆规作图，学生能够从几何的基本元素点和线入手，逐步构建出复杂的几何图形。点和线是几何的基础概念，理解两者之间的关系是学生掌握几何知识的基础。教师在教学过程中应结合尺规作图，通过理论引导与实际操作相结合的方式帮助学生理解几何中点与线的逻辑关系，并逐步培养其几何思维能力。

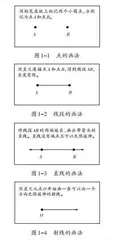
以人教版教材四年级上册“角的度量”单元中“线段、直线、射线”的教学为例，教师可通过实际作图引导学生理解线段、直线和射线的基本概念。如先在黑板上画出两个分散的点（如图1-1），向学生介绍点作为几何基本元素的特性——没有长度和宽度，并指出其在图形与几何中的重要性——是几何图形的起点。接着，用无刻度的直尺连接这两个点，得到一条线段（如图1-2），引导学生仔细观察，从而发现线段有两个端点且长度有限。最后，将线段的两端延长（如图1-3），引导学生理解直线的无限延伸性，使其明白线段和直线之间的差异。通过动态的演示，学生能够直观地掌握点、线段和直线的概念。在学生理解点、线段和直线的基本概念后，教师可引导学生理解射线的概念。先在纸上标记一个点O，然后用直尺过点O画出一条线段，最后将线段向一个方向延长，作出一条射线（如图1-4）。在此过程中，学生可直观看出射线的特性——有一个固定的起点，可以沿着一个方向无限延伸。为加深学生对射线的理解，教师还可以列举生活中的例子，如手电筒发出的光束属于射线。在学生掌握这些概念后，教师还可以设计一些实践性问题，帮助学生深化对几何知识的理解。如让学生用直尺作出两条相交的直线，并标记它们的交点，从而帮助学生理解直线相交的特性。通过作图活动，学生能够在实践中巩固线段、直线、射线的有关知识，同时在观察和思考中进一步理解它们之间的关系。

（二）以线制角，强化学生空间想象能力

画角是小学数学尺规作图教学的重要内容之一。使用无刻度的直尺和圆规进行实际操作，构建角的几何形状、探索角的特性，可以深化学生对角的理解。

以人教版教材四年级上册“角的度量”为例，首先，教师要帮助学生理解“角”的概念。如引导学生用无刻度的直尺作两条相交的直线，让学生认识到角是由两条有公共端点的射线构成的（如图2-1）。接着，利用圆规引导学生如何作出角：先用圆规以一点为圆心作一个圆，然后用直尺作一条经过圆心的直线，这条直线就构成了角的一条边，接着用圆规在圆上选择任意一点，用直尺连接该点与圆心即形成角的另一条边。通过该过程，学生能够直观地理解角的构造方法，并用圆规准确作出具有一定度数的几何角。最后，在构造角平分线时，教师可以引导学生以角的顶点O为圆心，用圆规画一个圆，与角的两边分别交于点P和点Q，再分别以点P和点Q为圆心，以大于[12]PQ的长度为半径画圆弧，两条圆弧相交于点C，连接点O和点C，那么OC即为[∠AOB]的角平分线（如图2-2）。

（三）以圆成方，锤炼学生耐心细致品质

“以圆成方”主要是利用圆规和无刻度直尺，帮助学生构造出正方形、长方形。通过“以圆成方”，学生能够理解正方形和长方形的几何特性，同时锤炼耐心和细致的品质。该教学策略依托圆的基本性质，通过圆规生成图形的基点，再利用直尺构造出符合几何规律的图形。以“圆”构造“方”的几何图形，能考查学生的操作能力，同时使其理解“方”形的对称性、边长关系和角度的特性。

例如，教学人教版教材三年级上册“长方形和正方形”时，教师可以引导学生通过尺规作图构造长方形：先用圆规以点[O]为圆心、[OA]为半径画一个圆，然后用直尺过圆心[O]画两条直径AB和CD，最后引导学生顺次连接圆周上的A，C，B，D四个点，线段AC，CB，BD和DA构成长方形ACBD（如图3）。

在“以圆成方”的尺规作图练习中，学生不断调整和确认作图细节，既提高了精确作图的能力，又培养了耐心。

在通过尺规作图构造正方形的教学中，教师还可以引导学生用圆规以点O为圆心，以OA为半径画一个圆，然后用直尺作两条过圆心O且互相垂直的直径AC和BD，最后用直尺顺次连接圆周上的A，B，C和D四个点，那么线段AB，BC，CD和DA构成正方形ACBD（如图4）。

（四）以形表意，激发学生数学应用意识

“以形表意”是指通过几何图形来表达实际意义，从而增强学生的数学应用意识。在尺规作图教学中，教师可以通过构建几何图形如长方形、正方形和圆，帮助学生掌握几何图形的基本特性，同时引导学生发现几何图形在日常生活中的广泛应用。无论是简单的平面图设计，还是复杂的建筑布局，几何图形都与现实世界紧密相连。教师可以设计实践性任务，引导学生运用几何图形解决实际问题，深化学生对数学知识的理解，增强学生将数学知识应用于生活的意识和能力。

例如，教师可以设计一个实际任务——设计一个小花园的平面图，引导学生结合所学的长方形、正方形等几何图形，利用尺规作图规划好花坛、草坪、步道等的形状和相对位置（如图5）。在学生完成作图后，教师还可以引导学生思考为什么选择特定的几何图形作为这些元素的形状，并鼓励其讨论如何提高空间的利用率。

通过完成实际任务，学生能够加深对几何图形的理解，同时亲身体验数学在实际规划中的应用，从而增强数学应用意识。

综上所述，尺规作图教学可以有效帮助学生更好地理解和掌握几何知识，同时促使其在实际问题中灵活应用所学知识，为后续的数学学习打下坚实基础。期待在未来的教学实践中能有更多的教师优化几何直观教学策略，为提升学生的数学素养做贡献。

［ 参 考 文 献 ］

[1] 顾兴德.小学数学教学中引进“尺规作图”的实践性研究[J].数学学习与研究，2024（14）：74-76.

[2] 顾晓东，沈晓东.小学阶段尺规作图的教学价值与实践策略[J].小学数学教育，2023（24）：4-5，8.

[3] 陈秋蓉.新课标视域下小学数学“尺规作图”教学实践[J].教育界，2024（20）：5-7.

[4] 林洁梅.小学“尺规作图”教学建构与实践[J].福建教育学院学报，2023，24（12）：87-89.

（责编    吴美玲）