核心素养背景下“平行四边形的面积”教学思考与改进
作者: 黄小民
[摘 要]在核心素养背景下,从面积本质出发教学,并对传统教学加以改进,着力沟通“数方格”与“图形转化”的内在联系,由理及法,能促进学生深度学习,培养学生量感,发展学生空间观念。
[关键词]平行四边形面积;数方格;量感
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2024)17-0039-03
“平行四边形的面积”是一节比较经典的课例,也是学习多边形面积的种子课,对今后三角形、梯形、圆等图形面积的学习都有着指导意义。在教学“平行四边形的面积”时,部分教师通常是先让学生分别数出方格纸上的长方形和平行四边形的面积并填写表格,然后引导学生观察比较、提出猜想,接着进行图形变换,观察它们的内在联系,最后推理得出平行四边形的面积计算公式。
一、课前思考
笔者觉得这种教学方法有3个地方值得讨论。
1. “数方格”环节只是为了“猜想”而设,没有将“数方格”作为核心内容来贯穿整个课堂教学过程,更没有沟通好“数方格”与“图形转化”的内在联系,导致后面“用割补法把平行四边形转化成长方形”没有真正成为学生学习的内在需求,也不利于学生量感的培养。
2.“不满一格的都按半格计数”得到的是估算结果,容易让学生由此猜测“平行四边形的面积=底×高”是不严谨的,从而对这一猜想产生怀疑。另外,有了这一提示之后,学生只会按照这一种方式去数,抑制了学生的个性思维和创新能力的培养,不利于学生数学活动经验的积累,更不利于转化思想的自然孕育。
3.受“长方形的面积=长×宽”结构性(邻边相乘)的干扰,许多学生会认为“平行四边形的面积=底×邻边”,这其实是一种负迁移。这种教学方法没有从源头上去防止这种负迁移的发生。
二、教学实践
在核心素养背景下,笔者重新审视了这节课,并根据以上3点思考,结合学情,对本课做了一些改进。
【改进一】巧铺方格,初步感知平行四边形的面积计算
1.大胆猜测,放手计算
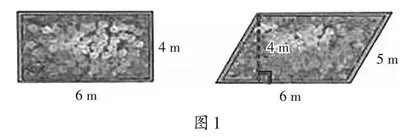
师(出示图1):下面两个花坛哪个大?你是怎么比较的?
生1:要先分别算它们的面积,再比较。
(学生很快算出了长方形的面积,但对平行四边形面积的计算感到困难。)
师:大家可以根据自己的理解大胆猜测,列式计算。
[笔者板书学生的四种不同计算方法:①5×4=20(m2),②6×4=24(m2),③6×5=30(m2),④6×5×4=120(m2)。]
2.巧铺方格,排除错误
师(出示图2):请大家仔细观察这个图形,对照你们列出的4种算法,说说哪种算法是错误的。为什么?
(每个格子边长为1 m)
生2:算法①错了。图中铺的格子每行有5个,共4行,面积是5×4=20(m2),但格子没有铺满图形,说明图形的面积比20m2大。
师(小结):分析得有道理,也就是说用“邻边×高”计算这个图形的面积是错的,排除!
师(出示图3):把两边空白的地方继续铺上方格,每行7个,铺了4行,面积是7×4=28(m2),但所铺的格子超出了图形范围,说明哪种算法也是错误的?为什么?
生3:算法③是错误的,因为30>28。
生4:算法④是错误的,因为120>28。
师(小结):看来,用“底×邻边”算这个图形的面积也是错的,“底×邻边×高”更是错得离谱。这两种算法都要排除。
生5:由前面的计算可知,这个图形的面积在20m2到28m2之间,只有算法②的结果符合。
师:那么平行四边形的面积究竟该怎么计算呢?
[设计意图]为使学生真正理解面积计算的本质,培养量感和推理意识,笔者先鼓励学生大胆猜测,放手计算,然后引导学生用数格子的方法逐一排除、去伪存真,真正从源头上防止学生产生“底×邻边”算面积的负迁移。
【改进二】自主数格,深入理解平行四边形的面积的本质
师(出示图4):请大家仔细观察,数一数,一共有多少个格子?
(每个格子边长为1 m)
生6:我先数整格的,有20个,再把左边不是整格的逐一平移到右边,刚好凑成4个整格。20+4=24,一共有24个格子。
生7:我先把左上角2个不是整格的一起平移到右上角,刚好凑成2个整格,再把左下角2个不是整格的一起平移到右下角,刚好也凑成2个整格。这样每行有6个格子,共4行,一共有6×4=24(个)格子。
生8:我还有更简单的方法。把平行四边形中虚线左边的三角形平移到右边,这样就一次性都凑成整格了。每行6个格子,有4行,一共有6×4=24(个)格子。
师:刚刚我们猜测这个平行四边形的面积可以通过算法②的算式计算。现在我们通过平移的方法得到每行有6个格子,共4行,一共有6×4=24(个)格子,也就是24m2,说明算法②的算式是正确的。
[设计意图]数方格算面积是图形面积计算的基本方法,即单位面积测量法,这种方法在学习长方形的面积计算时也曾使用过,但是如何数平行四边形的面积是一个新的问题。在这节课中,笔者删除了“不满一格的都按半格计数”这一提示。这样学生的思维不会受限,数的方法也多种多样,而且还考虑怎么凑出整格,真正体现了数方格的价值,孕育了转化思想,为学生进一步探索平行四边形的面积计算公式做了充足的准备。
【改进三】反思数格,有效沟通“数方格”与“图形转化”的内在联系
师:刚才我们用平移数格子的方法求平行四边形的面积,你认为哪种图形的面积与平行四边形的面积有关?猜一猜平行四边形的面积公式。
生9:我觉得长方形的面积与平行四边形的面积有关,因为我们刚刚在数格子的时候凑成整格,其实就是将图形变为长方形。
生10:我发现每行格子的边长总和等于平行四边形的底,每列格子的边长总和也刚好等于平行四边形的高,我猜平行四边形的面积计算公式应该是“底×高”。
生11:我发现计算平行四边形的面积与长方形的面积一样,都是相互垂直的一组对边的乘积。
[设计意图]数学的猜测从来都是有根据的,这体现了数学的严谨性。利用数方格的经验来猜测面积公式,是对学生量感培养的重大提升。通过反思数格子过程为整个图形的转化积累操作经验,使其成为学生学习的一种内在需求。
【改进四】多样操作,助力面积公式推导,拓展思维
1.动手操作,合作探究
出示合作探究要求:①想办法把平行四边形变成一个长方形;②观察转化前后的图形,你发现了什么?③想一想,怎样计算平行四边形的面积?
2.小组交流,推导公式
师:不数方格,你能算出平行四边形的面积吗?
生12:我们从它的顶点出发作高,然后沿着这条高剪下一个三角形,将这个三角形平移到另一边,这样图形就变成了一个长方形。
生13:我们没有从顶点画高,而是从中间作高,沿高剪开,也拼成了一个长方形。
生14:我们先把平行四边形上下对折,再沿着折痕剪开,但是怎么拼都是平行四边形。
生15:因为你们没有沿着高剪,剪出来的还是2个平行四边形,自然就拼不成长方形了。
师:虽然有的小组的剪法和拼法不同,但最终都是将平行四边形拼成长方形。现在再看看这些方法,它们有什么共同之处?
生16:都是沿着高剪开的,只有沿着高剪,才能剪出直角,拼成长方形。
师:为什么我们需要将其转换为长方形呢?
生17:因为长方形的面积我们已经学过,这样就可以通过求长方形的面积来求平行四边形的面积。
师:将平行四边形转化为长方形,只是形状变了,大小没有变化。以后学习梯形、三角形等图形的面积计算时,我们也可以把它们转化成学过的图形。这就是数学上的转化思想,即把未知的转化为已知的,从而解决问题!
(学生先观察转化前后的图形之间的内在关系,然后推导平行四边形的面积计算公式。)
[设计意图]学生自主操作,深刻领悟到割补法的多样性与直观性。利用几何直观,让学生用自己的语言有条理地说出推理的过程,既能让学生积累数学活动经验,又能渗透图形转化思想,让学生由此及彼、举一反三,发展思维。
三、教学反思
(一)追本溯源,突出本质
这节课主要围绕“如何计算平行四边形的面积”这一核心问题展开,面积与长度属于“图形的认识与测量”。求平行四边形的面积,本质就是度量平行四边形中包含多少个面积单位,因此要紧扣度量展开教学,让“数方格”贯穿教学始终。通过巧铺方格,让学生初步感知平行四边形的面积计算;通过自主数格,让学生直观感悟面积的度量就是面积单位的累加;通过数格,有效沟通“数方格”与“图形转化”的内在联系,为转化提供了直观支撑;最后更是将“割补法”作为一种快捷的计算平行四边形的面积的方法。
本节课的教学“源”于长方形,根据长方形面积公式进行构造并进一步整合到面积模型中,即将探究和推导长方形面积公式的方法、经验类推到平行四边形的面积计算中去。通过“大胆猜测,放手计算”这一环节的设计,让学生试错;通过“巧铺方格,排除错误”让学生知错、纠错;通过各种各样的数格操作,让学生理解计算平行四边形的面积本质是每行面积单位数与行数的乘积,与长方形一样,平行四边形的面积公式也是边长乘其对应边上的高,即“底×高”的乘积,从源头上防止学生产生“底×邻边”算面积的负迁移。
(二)结构地教,关联地学
《义务教育数学课程标准(2022年版)》提出要对课程内容进行结构化整合,探索发展学生核心素养的路径。在单元大概念的统领下,教师要站在学生学习的立场上,系统梳理课程内容,使已经学过的、正在学习的、将来要学的知识形成结构性的联系,使具体的内容学习不再单一和碎片化,让学生不断从整体上理解学习内容。
对于“平行四边形的面积”的教学,数学教师既要串联起面积概念、面积单位、长方形和平行四边形的面积计算方法等内容,形成知识方面的结构化,又要通过数方格,让学生感悟面积公式的本质——每行面积单位数与行数的乘积,并对照长方形和平行四边形的面积计算公式,使学生理解它们的面积计算都是互相垂直的一组线段的乘积,形成方法上的结构化。最终,教师可以依靠这一“结构化”,联“点”成“块”,联“块”成“网”,构建整个平面图形面积的知识框架,从而实现“教师有结构地教,学生有关联地学”。
(三)由理及法,发展量感
教学的最终目标是为了培养和提高学生的数学素养。本节课属于“图形与几何”领域下的“图形的认识与测量”内容,这一内容的核心素养主要体现在量感的培养上。量感主要是指对事物可测量的属性和大小关系的直观感知。学生量感的培养不是一朝一夕的事,需要一个长期的过程。小学阶段关于“图形的认识与测量”存在三个维度,分别是一维线的测量(本质是长度单位的累加)、二维面的测量(本质是面积单位的累加)和三维体的测量(本质是体积单位的累加)。从一维到二维再到三维,体现了测量本质的一致性,即都是度量单位的累加。教师不仅要把握好未知知识与已知知识的联系(正向迁移),使学生有更多的感悟与理解,还要找准知识的起点,抓住知识的本质,让学生动手操作,先感悟最基本的“理”(数线段算长度,数方格算面积,数方块算体积……),后形成简洁实用的“法”(周长公式、面积公式、体积公式……),最终赋予量感生长的力量,为学生素养的发展打下坚实的基础。
[ 参 考 文 献 ]
[1] 牛献礼. 以大观念为核心重构单元学习:“多边形的面积”单元整体教学的思考与实践[J].中国教师,2022(4):65-69.
[2] 李怀军,张维忠. 论数学素养培育的误区:以“平行四边形的面积”教学为例[J].当代教育与文化,2019,11(2):72-77.
(责编 覃小慧)