浅谈小学数学模型意识的培养策略

［摘 要］模型意识主要是指对数学模型普适性的初步感悟。文章以“相遇问题”为例，深入研究两个物体运动的多种情况，联系生活实际概括问题特点，在问题解决中提炼数量关系，结合运算律优化解题过程，构建相遇问题的解题模型，并拓展延伸至更复杂的相遇问题，培养学生模型意识。

［关键词］相遇问题；模型意识；小学数学

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）26-0068-03

模型意识主要体现在对数学模型的应用，它能够解决一类问题，是数学应用的基石。

“相遇问题”是苏教版教材四年级下册第六单元的教学内容。在此之前的学习中，学生已经初步掌握了使用列表法和画图法来整理条件和问题，并掌握了解决问题的一般步骤，掌握了“路程=速度×时间”以及“求两积之和（差）”等常见的数量关系。对于学生来说，如何在探索“相遇问题”的过程中构建数学模型，是学习本节课的重点和难点。本文以“相遇问题”为例，探讨数学模型意识的培养策略。

一、创设情境，初步感知问题模型

依据教材内容创设生动有趣的生活情境，不仅能够引导学生用数学的眼光观察生活，还能引导他们运用数学思维解决实际问题，实现数学与生活的有机结合。

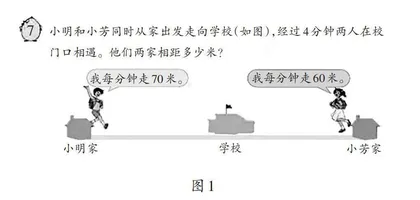
教材中的例题（如图1）是一个典型的相遇问题。在教学过程中，必须对这类典型例题进行深入的特点挖掘、解法探究和应用推广，以帮助学生巩固和深化相关概念，形成对例题的整体认识，还要引导学生从具体实例中抽象出一般规律，由特殊情形推广到一般情况，形成初步的模型意识。为此，笔者对这一例题进行了变式改进。

【教学案例】教材例题变式

小明和小芳同时从家出发走向学校（如图2）。猜一猜，他们可能怎么走？

变式后，由题可知两人的出发地点（异地）、出发时间（同时）、运动结果（到校），但是不知道学校的具体位置，所以无法判断两人的运动方向。因此，笔者引导学生结合线段图，分以下三种情况进行讨论。

1.如果学校在两人家的左侧（如图3），他们两人同向而行，向左走。

2.如果学校在两人家的右侧（如图4），他们两人同向而行，向右走。

3.如果学校在两人家的中间（如图5），他们两人面对面走。

首先，从图5入手，引导学生理解面对面行走亦称为相向而行，相向而行的双方最终会相遇。学生结合日常经验，明确了“同时”“同向”“相向”“相遇”等词语的含义，掌握了典型相遇问题的特征，即“从两地同时出发，面对面相向而行”，初步构建相遇问题的运动模型。

接着，补充条件“经过4分钟两人在校门口相遇”，鼓励学生根据这一信息提出数学问题，并尝试解决。由于学生已经掌握了单个物体行程问题的数量关系“路程=速度×时间”，他们能够提出诸如“从小明家（或小芳家）到学校的路程是多少米？”“他们两家相距多少米？”等问题。在尝试解决这些问题的过程中，学生发现还需要知道两人的速度，进而认识到“相遇问题”与已学的行程问题之间的区别在于相遇问题涉及两个物体的运动，研究的内容是速度之和，包含了两个物体的速度。

最后，进一步完善并梳理条件和问题，引导学生提炼自己的发现并生成一个完整的相遇问题，用数学语言表述，如：“小明和小芳早上同时从家出发走向学校，面对面相向而行，经过4分钟两人在校门口相遇。小明的行走速度是每分钟70米，小芳的行走速度是每分钟60米。他们两家相距多少米？”

在学生对相遇问题的基本特征有了初步理解的基础上，添加相应的数学信息，有助于学生将生活问题转化为数学问题，并构建起相遇问题的模型。

二、直观感知，尝试构建解题模型

相比一般行程问题，相遇问题涉及较多数学信息，数量关系较为复杂，学生往往难以迅速发现其中的联系。然而，通过运用已有的知识经验，学生可以在整理信息的过程中分析数量关系，在操作演示中感知数学模型，并在对比分析中归纳出解题的思路。可采取以下方法。

（一）情境再现

让两个学生分别扮演小明和小芳，模拟相遇的过程。这种情境再现不仅满足了学生喜爱游戏、乐于表现的心理需求，吸引了他们的注意力，而且在情境再现的过程中，能够重点突出相遇问题的四个基本要素，帮助学生更好地理解相关的关键词。

（二）摆纸条

提前准备两种规格的纸条若干，让学生根据题目条件摆一摆，这种方法直观明了。

（三）列表整理

整理信息（见表1），保留了速度和时间这两个核心数据，能分别算出两人从家到学校的路程，但是不能直接看出如何计算两家之间的路程。

（四）画线段图

通过数形结合的方式（如图6），可以直观清晰地展示数量之间的相等关系，即“小明的路程 + 小芳的路程 = 总路程”。

无论采用哪种方法，目的都是将抽象的问题具体化，将复杂的问题简单化，以便优化解题的途径。这有助于学生抽象思维和形象思维的协调发展，提高他们分析问题和解决问题的能力。

三、知识迁移，利用“旧模”建立“新模”

在尝试独立解决“两家相距多少米？”这个问题时，学生主要有两种解题方法：

①70×4+60×4                        ②（70+60）×4

=280+240                               =130×4

=520（米）                               =520（米）

方法①反映了线段图中各部分量与总量之间的关系，体现相遇问题的算式模型，即“速度1×时间+速度2×时间=总路程”。

对于方法②，从符号层面上来看，求两积之和算式的两个积中有一个乘数相同，可以逆向应用乘法分配律。从深层意义上解析，小明和小芳的速度之和为130米/分，将每分钟行走的130米视为一份，他们行走4分钟的路程就是4份。根据“每份量×份数=总量”的原则，相遇问题的模型也可以表述为“（速度1+速度2）×时间=总路程”，即抽象为乘法模型“速度和×时间=总路程”。

四、变式练习，在对比中巩固模型

不断变换相遇问题的条件，引导学生自主探究解法，发现解题规律，从变化中寻找不变，能巩固学生对相遇问题模型的理解。

（一）找准对应关系

【变式练习1】改变时间（仍同时出发）：将条件“经过4分钟两人相遇”改为“经过5分钟两人相遇”“经过10分钟两人相遇”“经过20分钟两人相遇”等。

【变式练习2】改变时间（不同时出发）：将条件“经过4分钟两人相遇”改为“若小芳比小明早出发1分钟，小明出发后再经过6分钟两人在校门口相遇”。

这两道变式练习均调整了相遇时间，但仍然遵循“路程1+路程2=总路程”或“速度和×时间=总路程”的模型，解决的关键在于厘清路程、不同速度及不同时间之间的对应关系。

（二）相遇问题模型延伸

【变式练习3】改变方向：将“同时从两地出发，面对面而行”改成“同时从某地出发，背对背而行”。

【变式练习4】改变路线（由“直线”改“环形”）：将问题条件设置为“两人在环形跑道上跑步，从同一地点出发，反向而行”。

这两道变式练习虽然不是典型的相遇问题，但都可以转化为典型相遇问题，或者沿用普通相遇问题的解题思路。

（三）灵活应用数量关系式

【变式练习5】变为求速度：已知总路程520米，相遇时间为4分钟，小明每分钟走70米，求小芳的速度。

【变式练习6】变为求时间：已知总路程520米，小明每分钟走70米，小芳每分钟走60米，求相遇时间。

这两道变式练习围绕相遇问题中的数量关系进行设计，已知其中几个量求未知量。

五、拓展延伸，体会相遇模型的广泛应用

（一）多次相遇

【应用1】A、B两地相距1200米，甲、乙两人分别从A、B两地同时出发，相向而行，在A、B两地间往返行走，甲步行的速度是每分钟40米，乙步行的速度是每分钟60米。请问几分钟后甲、乙两人第一次相遇？第二次相遇呢？

明确每次相遇时，甲、乙两人的总路程。甲、乙从两地相向而行，A、B两地的距离1200米是1个全程，第一次相遇共走1个全程；第二次相遇共走3个全程；第三次相遇共走5个全程……第n次相遇，共走2n-1个全程。

（二）中点相遇

【应用2】甲、乙两人同时从A、B两地出发，相向而行，在距离中点50米处相遇。已知甲的速度是每分钟100米，乙的速度是每分钟80米，他们从出发到相遇用时多少分钟？

在时间相同的情况下，速度越快，所走的路程越长，甲的速度大于乙的速度，意味着甲的路程超过总路程的一半，比总路程的一半多50米，同理乙的路程比总路程的一半少50米，甲乙的路程差为50+50=100（米）。实际上每分钟路程差为100-80=20（米），出发到相遇用时为100÷20=5（分）。

（三）折返相遇

【应用3】甲、乙两人同时从A地出发到B地。甲每分钟行50米，乙每分钟行60米，乙到达B地后立即返回。若两人从出发到相遇用了10分钟，则A、B 两地相距多少米？

甲、乙两人折返相遇，路程之和是2个A、B两地的距离，即（50+60）×10=1100（米）。A、B两地的距离为1100÷2=550（米）。

（四）联系生活

列举生活中类似“相遇问题”的情境，例如，购买上衣和裤子时，可以用“上衣的总价+裤子的总价=总价”计算，也可以把1件上衣和1条裤子看成1套，用“每套衣服的价格×套数=总价”计算。

由此可见，要培养学生的数学建模意识，教师就需要整体规划问题教学，让学生初步建构认知结构；引导学生对问题进行完整的数学表述；概括提炼一类问题的解题模型；应用模型解决更多问题。

（责编 杨偲培）