基于数学思想方法的单元整体教学探索

［摘 要］学生的整体认知结构不仅涵盖数学知识的系统架构，亦包含数学思想和数学方法，以及元认知等方面。在这一结构中，数学思想方法占据着至关重要的地位。文章以“圆”为例，通过分析教材内容、设计教学流程、实施教学方案等多个环节，探讨以数学思想方法为核心的单元整体教学模式。

［关键词］圆；数学思想方法；单元整体教学

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）26-0065-03

在设计教学内容时要突出核心内容，要呈现数学知识之间的内在关联，不仅要关注数学知识、数学技能的一致性，还要注重数学逻辑的连贯性，更要重视数学思想方法的一致性。因此，单元整体教学法的引入成为数学课堂教学的一种必然趋势。单元整体教学的内容可以是教材上的自然单元，也可以是以重要的数学概念为主线的单元，还可以是以数学思想方法为主线的单元。单元整体教学的核心目标是构建整体认知结构，不仅包含数学知识的整体架构，还涵盖数学思想方法与元认知等方面。在这些要素中，数学思想方法占据重要的位置，因此，在数学教学中，应当让学生自然地感受数学思想方法的发生与发展，并在单元整体教学的过程中习得这些方法，从而实现数学思想方法与单元整体教学的结合。本文以“圆”单元的整体教学为例，详细阐述具体的教学策略。

一、分析教学内容

（一）提炼核心问题

“圆”是小学阶段最后出现的一个平面图形，学生要在认识了常见平面图形和立体图形的基本特征、周长、面积的内涵，掌握了长度单位与面积单位后学习“圆”，为后续探究圆柱和圆锥奠定基础。“圆”这个单元包含认识圆的基本特征、圆的周长和面积公式推导、扇形的特征，这几个知识点都有一个核心问题——如何化曲为直（化圆为方）。

（二）寻找数学思想方法

解决核心问题的关键在于探寻隐藏其后的数学思想方法，并以此指导教学活动。通过分析“圆”这个单元的核心问题，可以发现共通的数学思想——“化曲为直”和极限思想，这些思想贯穿圆的基本特征、圆周率与圆周长的关系，以及圆的面积公式的推导等内容。

（三）重组相关内容

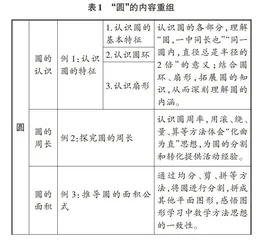
基于核心问题和数学思想方法，教师要对教学内容进行重组，以凸显单元知识的逻辑性和整体性。笔者从四个方面将教学内容进行重组（见表1）。

二、设计教学流程

（一）制订目标

单元整体教学目标并非课时教学目标的简单叠加，而是从单元整体出发，对知识、技能及数学思想方法进行综合考量，旨在提升学生的数学素养，实现单元整体教学的效果。因此，“圆”这一单元的整体教学目标可以这样确立：经历圆的特征、周长、面积的研究过程，体会转化思想；在“方中圆”与“圆中方”的学习中感受极限思想；经历知识与技能的形成过程，发展问题意识、反思意识和创新意识。

课时教学目标依据核心问题，在单元整体教学目标的指导下分阶段制订，分为知识技能目标（显性目标）和思想方法目标（隐性目标）（见表2）。

（二）收集素材

数学思想方法的形成离不开学习活动，学习活动的顺利开展离不开丰富的学习素材。因此，教师需要收集相关的数学史料，以丰富学生的学习内容。在“圆”的单元整体教学中，笔者选择了一些有关“圆”的数学史料（见表3）。

（三）预设活动

在预设活动时，不仅要关注各课时的独立性，还要关注数学思想方法在各课时中的递进关系，同时要考虑各课时学习活动的“承前启后”，考虑数学思想方法的迁移，以便在后续课程中运用同样的方法展开研究（主要预设教学活动见表4）。

三、实施教学方案

（一）体验思想——基于整体的感知

单元整体教学的起始课很重要，有提纲挈领的作用。教师应利用起始课帮助学生构建对单元知识点的整体认识，并让他们深入体会单元中蕴含的数学思想方法。例如，在“圆”单元的起始课“圆的认识”中，教师可以通过展示生活中的圆形实例，引导学生抽象出“圆”；随后，让学生尝试用不同的方法画圆，并比较使用生活素材画圆与用圆规画圆的异同，了解“圆，一中同长也”的含义，并探讨如何测量圆的周长。在这一过程中，学生初步感知“化曲为直”的思想，并为“曲”与“直”的转换做了理解基础。

（二）明确思想——基于概念的习得

在学生对“化曲为直”的思想有了初步感知之后，教师可以将圆定义为“从一点出发，引出无数条等长线段，连接这些线段的另一端点所形成的图形”。在这一过程中，“无数条”的概念实际上蕴含了极限思想。随着等长线段的增加，学生逐渐理解了“方”与“圆”的转化，并借助极限思想抽象出圆的定义与基本特征。

（三）巩固思想——基于知识的运用

明确了数学思想方法之后，教师应考查学生是否理解了这些思想方法，是否能在学习中自觉运用。在活动实施过程中，教师应鼓励学生有意识地运用转化思想。例如，在“圆的周长”一课中，学生可以借助“化曲为直”思想进行滚动、缠绕等操作，测量圆的周长，并计算圆周长与直径的比值。此时，教师可以引入刘徽的“割圆术”，让学生经历科学的圆周率探究过程，深刻体会极限思想的重要作用。

（四）发展思想——基于问题的解决

随着时代的发展，数学思想方法也在不断丰富。因此，教师应以发展的眼光看待数学思想方法，理解其综合性和深层次性。在“圆的面积”一课中，学生猜想推导圆的面积可能也需要进行转化。在具体的操作和对比中，学生发现分割的份数越多，拼成的图形就越精确；教师展示“切西瓜法”和“开普勒法”。在这个过程中，学生的思想发展经历了三个阶段：分割圆（从圆到方）→分割的份数越多，拼成的图形越精确（极限思想）→“切西瓜法”和“开普勒法”（转化思想与极限思想的融合）。

综上所述，借助单元整体教学可以更好地挖掘数学思想方法。教师要引导学生在单元整体教学中习得数学思想方法，充分发挥其在教学中的价值。

［ 参 考 文 献 ］

［1］ 李建良.以数学思想方法为核心的单元整体教学设计与实施[J].教学与管理，2024（11）：52-56.

［2］ 毛晓雪.小学数学实施单元整体教学法的策略探析[J].甘肃教育研究，2024（3）：103-105.

［3］ 周瑜芽.实施单元整体教学，培养学生核心素养[J].江西教育，2024（14）：28.

（责编 黄 露）