以函数为平台 探究动态三角形的面积

【摘要】数学教学活动注重启发式，激发学生学习兴趣，引发学生积极思考。本文取材于中考数学复习中抛物线与三角形的面积问题，层层递进，学生经历动手操作、计算、猜想、推理、验证等活动过程，让学生明确数学怎么学习，让自己做数学的思考者。

【关键词】数学活动  抛物线  三角形面积

【中图分类号】G633.6   【文献标识码】A 【文章编号】2095-3089（2023）03-0139-03

学生的学习“应当是一个生动活泼的、主动的和富有个性的过程。除接受学习外，动手实践、自主探索与合作交流同样是学习数学的重要方式。学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程”。而这些目标任务的实施就落到了教学的组织者、引导者、合作者——教师的身上。

当下初中学生的数学学习现状是时间更紧了，数学作业的量更大了，留给学生思考的时间、空间更少了。学生见识面比较狭窄，在数学学习上只有通过大量的刷题、做题，以期能在数学考试中取得好成绩。其本质又回归了“题海”战术，并不利于数学核心素养的养成。我们期望通过自己的课堂活动努力改变当前的现状，使数学课堂面向全体学生，适应学生个性的发展。

一、低起点，旨在激活原有知识

在初三中考的复习中抛物线与三角形的面积是一类常见的问题，特别是动态中研究三角形的面积是学生学习的难点，通过数学课堂活动的设计，让学生做懂一道题，知一类，会一片，也让教师的数学课堂活动有一个方向，有一点思考。

三角形的面积是平面几何面积中一个重要的概念，关联着平面图形中的重要元素——边与角。当三角形融入到坐标平面中的时候，三角形的顶点、边就更加活跃了，学生解决问题的难度相应地也增加了。下面的问题是我们在学习中常见的经典问题：

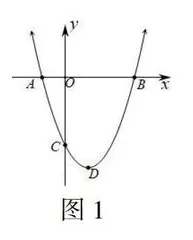
已知：如图1，二次函数y=x2-2x-3与x轴交于A、B两点（A在B的左侧），与y轴交于C点，顶点为D。（1）直接写出A，B，C，D各点坐标及直线BC表达式；（2）任取A，B，C，D，O中的三个点，求出能够组成三角形的面积。

题干先是给出了函数图形抛物线上的四个特殊点，要求学生求出四个特殊点的坐标，这些特殊点是三角形构成的基点，平面坐标系是三角形面积变化的平台，也考查了学生对函数抛物线图形的把控能力。对于第（2）题的解决学生表现出了强烈的求解欲和信心，可能学生不能找全所有的三角形，即使能找到三角形也不一定能求出它的面积。但是我们相信：学生学习数学的信心，是靠问题解决过程中的成功的体验来激发的。各个层次的学生都能动起手来，比如△AOC、△BOC、△ABC、△AOD、△BOD、△ABD、△OCD的面积学生都比较容易求出。为什么呢？要求学生及时地反思总结：因为这些三角形的底都在坐标轴上，底上的高根据点的坐标就可以表示出来。

学习能力比较强的学生在求△ACD与△BCD的面积时，表现出了解法的多样性，思维的发散性。先补后割的方法，学生求△BCD的面积给出了三种不同的方法如图2、图3、图4。学生通过补上的图形，使新的图形的边落在坐标轴上，从而便于求出图形的面积。特别是学生能从三角形的特殊性入手（如图5），发现△BCD是直角三角形，利用坐标平面中两点的距离公式求得三边长，进而求得三角形的面积。

二、铺台阶，构建知识之间的链接

教学时问题并没有结束，你还可以用什么方法来解决这个问题呢？马上引导学生阅读下面的材料，并根据阅读材料再求△BCD的面积。

通过阅读材料的铺垫，又唤起了学生求解坐标平面中三角形面积的欲望。问题的给出其实是学生学习新知识的过程，根据已经得出的结论学生能紧紧地抓住问题的关键点：铅垂高（h）和水平宽（a）。通过这个数学活动，激发了学生的数学学习兴趣，调动了学生的积极性。学生掌握了一种新的方法求面积，又引发了学生进一步对问题的思考。你能用同样的方法求△BCD的面积吗？

问题的解决简明扼要，给学生足够的时间、空间，让学生经历观察、猜想、模仿、计算、推理、验证等数学行为形成数学结论。通过学生的阅读理解创造一类求图形面积的新方法。学生类比迁移可以利用这个模型贯通这一类问题。

由动点而生成的三角形面积问题，是抛物线与直线结合的常见形式。解决这类问题上述的模型、方法，就体现了它的优势。

三、巧设问题，动静搭配，碰撞思维的火花

问题1：如图8，点P是直线BC下抛物线上的一个动点，是否存在点P，使△PBC与△DBC的面积相等？

中考的综合题中，动点的运动既会影响图形相关的数量关系，又会改变图形的位置及形状。在点的运动中要洞悉动点的运动轨迹、路径，关键是把图形的几何性质与点的坐标有机地结合起来。问题中△DBC是静态的，点P的运动改变了△PBC的形状和面积。首先要通过直观的方法引导学生在直线BC下方的抛物线上找到点P，使△PBC与△DBC的面积相等。其本质就是两个三角形同底等高，这样学生就能把动态变化的点转为求图中的定点。那就是过点D作直线BC的平行线，平行线与抛物线的交点就是所求的点P（如图9），学生动手操作，加强了问题解决的直观性，增加了学生思考的空间。

点的坐标是综合题的立足点（求函数表达式），又是综合题的制高点（求满足条件的点的坐标或存在性探究），求点的坐标一般要经历两个关键的步骤：定位与计算，在明确了点P的位置后，如何求出点P的坐标呢？通过图10发现，铅垂高和水平宽中的两个量，水平宽不变还是3，而铅垂高可以用动点的横坐标来表示，因为动点的路径就在抛物线上。

问题2：在直线BC上方的抛物线上是否存在点P，使△PBC与△DBC的面积相等？

由图11可知，在直线BC上方的抛物线上必定存在这样点：点P到直线BC的距离等于点D到直线BC的距离，利用三角形面积等底同高的的方法可以找到两个点。如何确定这两个点的坐标呢？直接去求点D到直线BC的距离，可能行不通，能否换个角度去思考问题。如图12可引导学生从直线DP与y轴的交点N入手，从而确定直线BC到直线DP向下平移了几个单位。这样只要把直线BC向上平移相应的单位数就可以了。

黄东坡曾经在数学问题的解决中指出要从分析出发，从数学知识方法出发，使得每步之间都是思维行动的自然进发，这也是提高解题能力的关键。由形定数，由形思数，由数解形，巧妙地进行“数”与“形”的结合。学生在解题的过程中无形地渗透了“数形结合”的思想，提高了学生解题的能力，获得了数学学习的方法。

问题3：点P是直线BC下抛物线上的一个动点，是否存在点P，使△PBC的面积取到最大值？

由图9可知抛物线上点D、P到直线BC的距离相等，直线还可以向下平移，并且能够做到直线与抛物线相交于一个点Q（如图13），即直线与抛物线相切。此时在直线下方的抛物线上，点Q离直线BC的距离最大，点P只要移到Q点，△PBC的面积就能取到最大值。这样动态的点就可以确定下来了，引导学生借助方程组解的唯一性求得直线的表达式，进而求得方程组的解，最后得到点P的坐标。也可以让学生动手在图中找出使△PBC的面积达到最大值的点Q，那么如何求出确定的点坐标呢？借助图10求△PBC的面积的启发，把动点P的坐标设为动态的坐标，借助二次函数的最大值求得相应的x的值。

四、教学的反思

问题的设计摒弃了传统的以题论题，由浅入深，由易到难。让学生亲自动手操作画图，通过精确的数据计算，进行合理的猜想，形成有效的数学模型，并让学生运用模型去解决问题，有力地体现了数学的应用价值，让学生体验数学学习的成功乐趣。

层层变式，逐步深入，在数学问题的解决过程中学习数学知识，掌握数学学习的方法。我们期望通过有效的数学课堂活动设计，让我们的数学学习摆脱单纯的“题海战术”。这就需要我们结合学生数学学习的特点，遵循学生的认知规律和心理特征，激发学生的学习兴趣，引发数学思考；并能充分考虑数学本身的特点，体现数学的实质；在呈现作为知识与技能的数学结果的同时，重视学生已有的经验，使学生从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题。

参考文献：

[1]黄东坡.探究应用新思维[M].湖北：湖北人民出版社出版，2005.

[2]史宁中.义务教育数学课程标准（2011年版）解读[M].北京：北京师范大学出版社，2012.