初中数学图形旋转教学中“瓜豆原理”的应用及反思

摘 要：“瓜豆原理”能够帮助学生更好地理解旋转知识。文章探讨了“瓜豆原理”在初中数学图形旋转教学中的应用及反思，阐述了“瓜豆原理”的基本概念及应用原理，分析了“瓜豆原理”在旋转概念理解、旋转中心与旋转角度展示、旋转对称性理解、旋转与平移组合变换以及旋转图形面积与周长计算等方面的具体应用，并对“瓜豆原理”在教学中的适用性、局限性、实施方式以及评估与反馈机制进行了深入反思。

关键词：初中数学；图形旋转教学；“瓜豆原理”

“瓜豆原理”作为初中数学几何教学中的一个重要应用，具有广泛的教育意义和实际价值。旋转是重要的数学变换，也是初中数学中的重要内容，对于培养学生的空间想象力和几何直觉具有重要意义。但是，旋转概念的抽象性和复杂性使学生在学习过程中不容易理解。为了帮助学生更好地理解和掌握旋转知识，笔者在教学中引入“瓜豆原理”，通过构建具体的“瓜豆”模型，学生可直观地看到旋转过程中图形的变化，从而加深对旋转概念的理解。这为图形旋转教学提供新的思路和方法。

一、“瓜豆原理”的基本概念及其在图形旋转教学中的应用原理

（一）“瓜豆原理”的基本概念

“瓜豆原理”是基于几何变换中的比例和角度关系。具体来说，该原理涉及三个关键要素：定点、动点和它们之间的比例与角度关系。定点是旋转的中心或参考点，动点是围绕定点运动的点，比例关系指的是两个动点到定点的距离之比保持恒定，而角度关系是指这两个动点与定点连线之间的夹角保持固定。在“瓜豆原理”中，一个动点（主动图形，通常被称为“瓜”）的运动轨迹决定了另一个动点（从动图形，通常被称为“豆”）的运动轨迹。当“瓜”在直线上运动时，“豆”也将沿着相同的直线运动；当“瓜”在圆周上运动时，“豆”也将沿着相同的圆周运动。这种一致性是由它们到定点的距离比和夹角关系所保证的。

（二）“瓜豆原理”在图形旋转教学中的应用原理

“瓜豆原理”为图形旋转教学提供了直观且易于理解的模型。通过构建“瓜豆”模型，可帮助学生清晰地看到旋转中心、旋转角度以及旋转后的图形变化等关键要素，有助于学生更好地理解和掌握旋转概念。“瓜豆原理”强调了比例和角度关系在旋转中的重要性。在旋转过程中，两个动点到定点的距离比和夹角关系保持不变。通过引导学生关注这些关系，可帮助学生更加深入地理解旋转的规律，从而提高学生解决旋转问题的能力。“瓜豆原理”还为学生提供了探索旋转性质的平台，通过构建不同的“瓜豆”模型，学生可自主发现旋转图形的对称性和不变性等性质，从而培养他们的几何直觉和推理能力。

二、“瓜豆原理”在初中数学图形旋转教学中的应用

（一）“瓜豆原理”在旋转概念理解中的应用

在初中数学中，为帮助学生更好地理解和掌握旋转概念，教师可运用“瓜豆原理”。这一原理将旋转过程比作瓜和豆的关系，想象一个瓜（主动图形）和一个豆（从动点或图形），当瓜绕某点（旋转中心）旋转一定角度时，豆也会按照相同的角度绕同一中心旋转。例如，在解决关于三角形绕某点旋转的题目时，可以让学生想象三角形是一个“瓜”，而三角形的一个顶点或一条边上的某个点作为“豆”。当三角形绕某点（如顶点A）旋转45度时，学生需要理解并计算出“豆”（如顶点B或C，或BC边上的一点D）的新位置。通过“瓜豆原理”，学生能直观地看到，无论“瓜”如何旋转，“豆”总是以相同的角度和相同的方向跟随旋转，从而加深对旋转概念的理解。

（二）利用“瓜豆原理”直观展示旋转中心与旋转角度

为了让学生更直观地理解旋转中心与旋转角度的概念，我们可以利用“瓜豆原理”进行演示。在课堂上，我们可以使用教具或多媒体工具，展示一个图形（如圆形、三角形等）绕某一固定点（旋转中心）旋转的过程。例如，在解决关于圆绕圆心旋转的题目时，可以将圆看作“瓜”，圆心作为旋转中心，圆上的任意一点作为“豆”。当圆绕圆心旋转60度时，学生可以看到，圆上的每个点（包括“豆”）都绕圆心旋转了60度。通过这种方法，学生能直观地理解旋转中心和旋转角度的概念，还能学会如何计算旋转后图形的位置。

（三）“瓜豆原理”在旋转问题解决中的应用

在解决旋转问题时，“瓜豆原理”提供了直观且有效的方法。通过这一原理，学生可以将复杂的旋转问题简化为简单的角度和位置计算。例如，在解决一道关于线段绕某点旋转后长度的题目时，可以将线段看作“瓜”，线段的一个端点作为旋转中心，另一个端点作为“豆”。如人教版九年级上册第70页第7题：

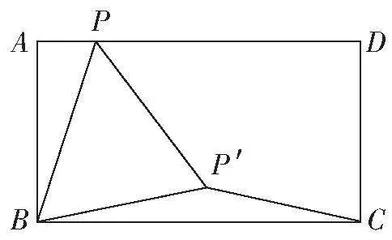
如图，在矩形ABCD中，BC＝2AB，P为边AD上的一个动点，线段BP绕点B顺时针旋转60°得到线段BP′，连接PP′，CP′。

（1）当点P′落在边BC上时，∠PP′C的度数为          ；

（2）当线段CP′的长度最小时，∠PP′C的度数为          。

第一问比较直接，当点P′落在BC上时，可以得到∠PP′C＝120°。

第二问有一定难度，因为要得到CP′的最小值需要确定点P′的运动轨迹，然后再利用垂线段最短，确定CP′的最小值，求出此时∠PP′C的度数。这个就是我们的瓜豆原理了。本题中可以看出P为主动点，P′为从动点，∠PBP′＝60°是定值。

通过上边的图，很明显观察到点P的轨迹是线段，那么P′的轨迹也同样是线段，那么就可以得到当CP′与点P′的轨迹垂直时最小，因为垂线段最短。此时只需要画出图形，通过证明得出△BAP ≌△BOP′，故有△BOP′是等腰直角三角形，∠OP′B是45°，所以∠PP′C＝∠OP′B＋∠OP′C－∠PP′B＝45°＋90°－60°＝75°。

这种方法简化了计算过程，有效提高了学生的解题效率。

（四）“瓜豆原理”在旋转与平移组合变换中的应用

在实际数学问题中，图形不仅涉及旋转，还涉及平移等组合变换。通过“瓜豆原理”，可以帮助学生更好地理解和解决这类问题。例如，在解决关于图形先旋转后平移的题目时，可以将图形看作一个“瓜”，旋转中心和平移方向上的某个点分别作为“瓜”和“豆”的初始位置。根据题目要求将“瓜”绕旋转中心旋转一定角度，得到旋转后的图形，再将旋转后的图形沿平移方向平移一定距离，得到最终的图形。在这个过程中，“豆”也会跟随“瓜”进行相同的旋转和平移变换。这样学生就可更清晰地看到旋转和平移的组合变换过程，从而更好地理解和解决这类问题。

（五）“瓜豆原理”在旋转图形面积与周长计算中的应用

在计算旋转图形的面积和周长时，“瓜豆原理”同样可以发挥重要作用。通过这一原理，可以将复杂的旋转图形简化为更简单的图形进行计算。例如，在解决关于三角形绕某点旋转后面积和周长的题目时，可以将三角形看作一个“瓜”，旋转中心作为定点，三角形的三个顶点作为“豆”。当三角形绕旋转中心旋转一定角度后，虽然图形的形状发生了变化，但面积和周长等属性仍然可以通过“瓜豆原理”进行计算。具体来说，可以将旋转后的图形看作是由原图形经过一系列简单的旋转和平移变换得到的，因此可以通过计算原图形的面积和周长，再结合旋转和平移的性质进行修正，得到旋转后图形的面积和周长。这种方法能简化计算过程，提高学生的解题效率和准确性。

三、初中数学图形旋转教学中“瓜豆原理”的反思

在初中数学图形旋转教学中，“瓜豆原理”的运用，能为学生提供深入理解旋转知识的新视角。但在实际应用过程中，教师也需要对这一原理进行反思，以更好地发挥在教学中的价值。

首先，需要反思“瓜豆原理”在教学中的适用性。虽然有助于学生理解旋转中心、旋转角度以及旋转后的图形变化等方面，但它并非适用于所有类型的旋转问题。在教学过程中，教师需灵活选择教学方法，根据问题的具体类型和难度，结合“瓜豆原理”与其他教学策略，以取得最佳的教学效果。其次，需要反思“瓜豆原理”在教学中的局限性。尽管这一原理能够帮助学生直观地理解旋转现象，但它可能无法完全揭示旋转背后的数学原理和逻辑。因此，在教学过程中，教师需要引导学生深入探究旋转的本质和规律，培养他们的抽象思维和逻辑推理能力。最后，需要反思“瓜豆原理”在教学中的实施方式。教师可通过构建具体的“瓜豆”模型、利用多媒体工具演示以及组织学生动手操作等方式实施“瓜豆原理”，但不同的实施方式对学生的学习效果产生不同的影响。因此，教师需要不断优化教学方法，以更好地激发学生的学习兴趣和积极性。

总之，“瓜豆原理”在形式上和解法上给我们提供了简单而又易操作的解题方法。“瓜豆原理”在初中数学图形旋转教学中的应用，不仅有助于学生理解和掌握旋转概念，还能提高他们的解题能力和数学思维能力。通过这一原理的引导，学生可以将抽象的旋转问题转化为直观的图形和角度计算，从而更深入地理解旋转的奥秘。但在实际应用中，需要注意其适用性和局限性，并根据问题的具体类型和难度灵活选择教学方法。教师还需要不断探索和优化教学方法，以激发学生的学习兴趣和积极性，提高他们的学习效率。

参考文献：

［1］王莉.初中数学几何教学中“瓜豆原理”的应用［J］.数理天地（初中版），2024（09）.

［2］许志强.巧用瓜豆原理，破解初中数学路径问题［J］.中学数学，2023（10）.