“双减”政策下的课堂教学

“双减”是指全面压减作业总量和时长，减轻学生过重作业负担，要求分类明确作业总量。对于初中学生来说，想要学习好数学需要多练、多思，但是“双减”政策下，数学的作业量明显比以往减少，打破了以往的熟能生巧的学习方法，学生不能仅通过大量的练习来巩固知识点，教师要让学生牢记知识点和课后精简的作业题目以巩固知识。

一、教材分析

“图形的初步知识”使学生进入平面几何的学习。“余角和补角”是“图形的初步知识”的重要组成部分，从线段的概念引出射线的概念进而引入角的概念，在学生认识直角、平角，比较角的大小后，再学习余角、补角的概念及性质。这是实验几何逐渐向证明几何的过渡，为以后证明角的相等作铺垫，也是为培养和发展学生的逻辑思维能力、观察分析能力、演绎归纳能力打基础。

二、教学目标

1. 知识与技能目标：在具体情境中了解余角与补角，理解余角与补角的性质，通过练习掌握其概念及性质，并能运用知识来解决一些简单实际问题;

2. 过程和方法目标：经历观察、探究、操作等过程，发展学生几何概念，培养学生推理能力和表达能力;

3. 情感态度与价值观目标：培养学生乐于探究、合作的习惯，体验探索成功，感受到成功的乐趣，进一步体会“数学就在我的身边”，增强学生用数学知识解决实际问题的意识。

三、教学重点

余角和补角的概念可在教学时运用文字语言、图形语言、符号语言三者结合的训练方法强调概念的本质特征，突出教学重点。

四、教学难点

关于余角和补角的应用，常常需要说理，或综合运用代数知识，特别是用代数的方法来计算角的度数。由于学生缺乏经验，难以灵活应用，是教学中的难点。教师可通过由浅入深、讨论比较、归纳小结等方法及变式训练突破上述难点。

五、教学过程

1. 课前完成“余角和补角”的预习题目

2. 趣味导入——折纸

向学生展示一张长方形纸片，沿一个角折叠后，折痕与长方形的边形成了角的数量，得出这些角有怎样的数量关系。最后介绍这节课学习的内容——“余角和补角”。

3. 得出概念

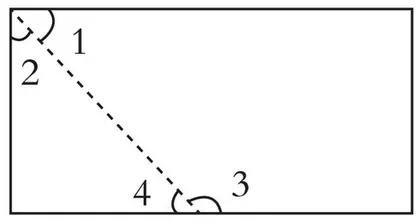
通过折纸活动中角的数量关系可以得出余角的概念：如果两个角的和等于90°，就说这两个角互为余角（简称为两个角互余）。如图，可以说∠1是∠2的余角，或∠2是∠1的余角，或∠1和∠2互余;同理得出补角的概念：如果两个角的和等于180°，就说这两个角互为补角（简称为两个角互补）。如图，可以说∠3是∠4的补角，或∠4是∠3的补角，或∠3和∠4互补。

4. 得出性质

首先，请学生思考：如下图∠BOD=90°，∠1和∠2互余;∠AOC=90°，∠1和∠3互余，那么∠2和∠3有什么关系？

引导学生推理：因为∠1+∠2=90°，所以∠2=90°-∠1;因为∠1+∠3=90°，所以∠3=90°-∠1;所以∠2=∠3，得出同角的余角相等。

在证明等角的余角相等时，给出以下条件：如图，∠1和∠2互余，∠3和∠4互余，假设∠1=∠3，那么∠2=∠4吗？为什么？

仿照上面的推理过程：因为∠1+∠2=90°，所以∠2=90°-∠1;因为∠3+∠4=90°，所以∠4=90°-∠3，又因为∠1=∠3，所以∠2=∠4，所以得出等角的余角相等。

学生通过教师的引导和自己的推理，更容易理解余角的性质：同角或等角的余角相等。因此在学习补角的性质时，学生有了对余角性质的推理经验，在研学案的引领下，引导学生得出补角的性质：同角或等角的补角相等。

5. 练习典型习题，牢记知识点

学好数学的有效方法是学练结合。在本次教学中，笔者主要设计以下典型练习题，让学生及时掌握知识点。

（1）已知∠1=20°，∠2=30°，∠3=60°，∠4=150°，则∠2的余角是___，∠4的补角是___。（  ）

A. ∠2，∠2 B. ∠3，∠2

C. ∠1，∠2 D. ∠4，∠1

（2）若∠1与∠2互余，∠2与∠3互余，则_____ _____，根据是_____。（  ）

A. ∠1=∠3， 同角的补角相等

B. ∠2=∠3， 同角的余角相等

C. ∠1=∠3， 同角的余角相等

D. ∠1=∠2， 同角的余角相等

（3）已知∠A与∠B互余，且∠A的度数比∠B度数的3倍还多30°，求∠B的度数。

6. 课后作业

（1）已知∠A=35°，则∠A余角的度数是（  ）。

A. 55° B. 45°

C. 145° D. 135°

（2）下列说法正确的是（  ）

A. 一个角的补角一定大于它本身

B. 一个角的余角一定小于它本身

C. 一个钝角减去一个锐角的差一定是一个锐角

D. 一个角的余角一定小于其补角

（3）如图，将一副三角尺按不同的位置摆放，下列方式中∠α与∠β互余的是（ ）

A. 图① B. 图②

C. 图③ D. 图④

（4）∠α=35°，则∠α的补角为______度。

六、教学效果

1. 活动导入简练

本次课程带领学生以折纸形式进行导入，得出折痕与长方形的边所形成的角的数量，以及角的数量关系，从而让学生知道本次课程主要围绕这几个角进行学习，从而得出互余、互补的概念。而传统的教学导入方法是通过直角三角板得出两个锐角相加等于90°，进而得出互余的概念，互补的概念又要通过其他例子来引导。

2. 推导过程时讲练结合

能够让学生记住知识点最好的方法就是让他们自己做一遍。在本次的性质推理过程中，笔者先推理同角的余角相等，然后与学生一起推理等角的余角相等，从而得出同角或等角的余角相等。通过对余角性质的推理，学生按照这样的推理思路，能够准确快速推导出同角或等角的补角相等。

3. 典型习题分层次

课堂习题分为A、B两个层次，难度有递进关系，引导学生形成明确的解题思路，教师讲解例题，学生通过做题进一步巩固知识点。

4. 优化作业设计

“双减”政策下，作业量控制在20分钟内，要考虑优生、中等生、学困生的作业情况，因此本次作业设计为8道题目，来源于对课本题目的改编、期末考题，以基础题目为主。