指向能力提升的初中数学作业设计创新

初中数学教师应不断提高自身的专业素养和教学水平，创新作业设计方式方法，更好地服务于学生的能力提升和全面发展。本文以“几何图形”作业设计为例，就初中数学作业设计的创新策略作探讨。

一、探究型作业，培养科学探究能力

探究型作业旨在培养学生的逻辑思维和创新能力。学生在完成这类作业时，可以通过主动探索、发现规律、解决问题，加深对数学知识的理解，培养合情的推理能力。教师在设计此类作业时可以适当提高难度，使学生感到有挑战性，激发他们的求知欲。在引导学生探究时，教师需注意过程和方式方法，着重培养学生的探究能力。

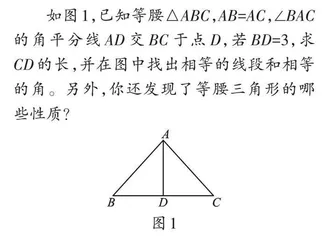
如图1，已知等腰△ABC，AB=AC，∠BAC的角平分线AD交BC于点D，若BD=3，求CD的长，并在图中找出相等的线段和相等的角。另外，你还发现了等腰三角形的哪些性质？

本题主要目的是让学生运用等腰三角形“三线合一”以及“等边对等角”的性质来解决问题，要求学生从给定的条件出发，通过几何定理和推理，找出相等的线段和角。题目最后一问“你还发现了等腰三角形的哪些性质”具有一定的开放性，学生需要在已有知识的基础上，进一步思考和探索等腰三角形可能具有的其他性质。

推理和探索的过程能够激发学生的探究欲望，促使他们主动地挖掘和总结所学知识，提升归纳和总结能力。开放性问题促使学生主动思考和探索，这个过程不仅仅是解决一个题目，而是从中学到如何挖掘知识背后的更多内容。科学探究能力是学生未来发展必备的关键能力，教师对学生的引导和有效训练至关重要。

二、个性化作业，满足不同学生的学习需求

每一名学生都具有独特的个性，思维方式和对知识的接受能力是不一样的，这就造成了学生在学习知识时会产生差异性和层次化的局面。因此，教师在设计初中数学作业时，也要考虑不同学生的学习实际，注意层次性。

如图2，在平面直角坐标系xOy中，有一个Rt△AOB，点A （0，4），点B （8，0）。以点O为圆心，半径为r作圆O。

（1） 当圆O与直线AB相切时，求半径r的值。

（2） 若圆O与直角三角形AOB的三边共有4个交点，求半径r的取值范围。

（3） 当r=3时，将圆O沿x轴正方向平移，设平移的距离为m（0≤m≤8） 。在平移过程中，圆O与△AOB的公共点个数会发生变化，求公共点个数分别为3、4时，m的取值范围。

这道题由多个小问题组成，从基础的求解半径，到基于给定条件求半径的取值范围，再到圆与三角形三边交点个数的讨论，层层递进。并且题目结合了直角三角形、圆、切线、平面直角坐标系等多个几何元素，要求学生能够灵活运用这些图形的性质来解决问题。

基础稍弱的学生，可以尝试独立解决前面较为基础的证明问题，然后再和其他学生合作解决后面的问题，这不仅能够激发自信心，合作探究能力也得以培养。题目综合了多种几何图形的性质，能够让学生感受到几何知识之间的内在联系，从而培养学生的几何观念和空间观念。

三、学科融合型作业，提升综合应用能力

将不同学科的知识和技能进行整合，能够帮助学生形成完整的知识体系，增强对知识的理解。教师在设计作业时可以通过引导学生结合数学与其他学科知识去思考问题，强化学生对数学知识的掌握，拓展学生对知识运用的广度，让学生在跨学科的情境中，锻炼解决问题的能力，进而培养其综合素养。

如图3，水平桌面上放置一块平面镜 PQ，点光源 S 位于平面镜上方。点光源 S 发出的一条光线 SA 射在平面镜 PQ 上，入射点为点 A，入射角为 30°，已知点 S 到平面镜 PQ的垂直距离 SO=4m，在平面镜 PQ 上取一点 B，连接 SB，使得△SAB 的面积为 8[3]，求反射光线 AC 与直线 SB 所成夹角的度数。

本题主要让学生运用数学中的三角形面积公式和物理中光的反射定律来解决问题。学生需从给定条件出发，通过面积公式计算出相关边长，再结合物理中光的反射原理得出角度关系。

学生通过对已知条件的分析和运用，不仅加深了对相关知识的理解和记忆，在推理和探索过程中，逻辑思维和跨学科应用能力也得到了锻炼。并且在解决这类问题时，学生会经历观察、猜想、证明的推理过程，在运用已有知识探索新知的过程中，体验到逻辑论证的乐趣，感受到跨学科知识融合的魅力，进一步激发学习热情。

作业的设计对学生的发展至关重要，教师只有以生为本，以研究者的视角设计丰富多样的作业，才能满足不同学生的学习需要，使得学生的各项能力得到锻炼，才能促进学生全面发展，助力学科育人目标的实现。

（作者单位：江苏省徐州市徐庄中学）