有效“沟通”高效计算

摘要：一年级学生在碰到填空式计算题时，出错率比较高。究其原因，主要是学生不会逆向思考，只会机械计算。为了提高学生填空式计算题的正确率，文章对我校一年级学生进行了为期一年的实践研究。通过“梳理教材，筛选典型习题；前后联系，确定渗透起点；精心设计，探索课堂模型；逐步渗透，巩固解决方法”这四个策略，有效地“沟通”了算式各部分与“部总关系”之间的联系，探索出了一套运用“部总关系”来解决填空式计算题出错率高的解题模式。

关键词：填空式计算题；渗透；数量关系

中图分类号：g623.5文献标识码：a文章编号：1673-8918（2025）05-0065-04

一、 点击现状

开学初，笔者对我校二年级学生进行了测试，共4部分，第1、2部分为一般口算题，第3、4部分为填空式计算题。此次检测卷下发443份，收回443份。从收回的检测卷中，我们发现第1部分和第2部分的正确率最高，分别达到了92.3%和 93.5%；第3部分和第4部分的正确率明显比较低，分别只有 84.6%和83.9%。从此次检测结果可以看出，一年级学生在填空式计算题的计算方面还有困难。

二、 剖析原因

【原因一】教师没有专门开设专题课

通读人教版一年级教材，笔者发现教材中并没有设置“填空式计算题”的相关内容，数学教师也就不会开设“填空式计算题”的专题课，只有当练习中出现此类问题才会简单地讲解，而且讲解的方法也没有统一标准。

【原因二】教师没有渗透好数量关系

数学教师在教学填空式计算题时，会教学生一些计算技巧，并加以强化训练，但是学生只会计算却不明白其所以然，教师没有渗透好数量关系。

计算教学在小学数学教学中有着十分重要的地位，这在课时比例中得到充分的体现。四则计算中的符号“+-×÷”，其意义本质就是量与量之间的关系，即数量关系。其实，从学生认识与实施教学的角度讲，应该是先认识数量关系，再根据关系运用计算方法，但实际上我们发现学生“认识数量关系”与“运用计算方法”之间是严重脱钩的，从而导致填空式计算题正确率低。

所以，我们有必要顺着“总数与部分数关系”到“加、减关系”，开展相互渗透研究，从而从本源上解决“填空式计算题正确率低”的问题。

三、 策略研究

（一）梳理教材，筛选典型习题

通读教材一年级教材，笔者发现，教材中涉及的数量关系有部总关系和相差关系，而相差关系又可以归类到部总关系，把相差关系归类到部总关系可参考以下具体操作。

精读人教版一年级教材，笔者发现，教材中涉及的填空式计算题的习题比较少。特别是一年级上册，涉及的全部都是加法类的，如7+=17。一年级下册涉及的就更少了，只有三题是减法类的，分别为：50=51-、60=62-和-50=16。通过筛选和归类，一年级涉及的填空式计算题有三类：7+=17、50-=20、-50=16，即加法算式中求加数、减法算式中求减数和减法算式中求被减数，因此我们只要知道这三类题目所对应的数量关系就可以了。

（二）前后联系，确定渗透起点

1. 追根溯源——挖掘“部总关系”的原型

通读教材，笔者发现一年级上册第21页就有了部总关系的原型（如下图）。但是此时学生还没开始学习加法和减法，所以不宜过早地渗透数量关系“部分数+部分数=总数”和“总数-部分数=部分数”（简称“部总关系”）的教学，但笔者认为可以让学生初步认识“部总关系”中各部分名称。

教学《分与合》一课时，笔者引导学生在分5个玉米的过程中初步认识了“部分数”和“总数”，让他们知道两个“部分数”和“总数”之间的关系。即：

为之后教学“部总关系”打好基础，即“部总关系”的原型就是“数的分与合”。

2. 提前渗透——构建“部总关系”的雏形

一年级上册第24页和第26页正式引入了加法和减法，笔者认为可以开始教学“部总关系”了。笔者在教学一年级上册《加法》和《减法》这两节计算课的起始课时，让学生在头脑中加深了对“部分数”和“总数”这两个抽象概念的认识。首先，笔者需引导学生正确区分加、减法中的三个数分别代表“部总关系”中的哪部分，如先找到“总数”（一般来说是最大的数），那么剩下的两个数就都是“部分数”了（一般来说是较小的两个数）。其次，笔者引导学生用“+”和“-”把“部总关系”中的三部分名称连接起来，得到完整的“部总关系”——“部分数+部分数=总数”和“总数-部分数=部分数”。

（三）逐步渗透，巩固计算方法

通过《分与合》的学习，学生认识了“部总关系”中的“部分数”和“总数”；通过《加法》和《减法》的学习，学生在脑海里初步建立了“部总关系”的雏形。笔者认为，从计算类解决问题的起始课就应该渗透“部总关系”的教学。那么，如何在平常教学中逐步渗透数量呢？笔者认为可以从以下两个方面展开：

1. 画一画，构建“部总关系”模型

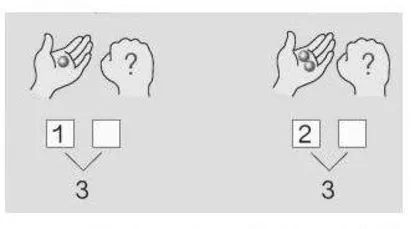
计算类解决问题的起始课有两节：一年级上册第45页求“总数”和一年级上册第46页求“部分数”。这两节课的共同点是问题蕴含在图中，图中还出现了帮助理解的特定符号——“”和“？”，而且这两个特定符号刚好又能和学生的前知识——《数的分与合》进行有效的沟通。笔者在教学这两节课时，是对比着进行的，其中渗透“部总关系”的方法也有相同的地方。首先，笔者认为两节课都需要用“画一画”的方法把形象具体的东西跟抽象的“部总关系”的三部分衔接起来，再用上面提到的两个特定符号沟通新旧知识的联系。最终得出：求总数用加法，求部分数用减法来解决这两类问题。如下图：

2. 比一比，转化“相差关系”模型

教材中涉及的数量关系还有“相差关系”，人教版一年级下册第21页例6就是“相差关系”模型建立的新授课。“较大数-较小数=相差数”这个“相差关系”模型该如何理解呢？笔者认为，学生可以通过“画一画”把“相差关系”成功转化为“部总关系”。如下图：

其实，“相差关系”模型本身与“部总关系”模型就存在着联系，笔者只是把它们进行了沟通。“相差关系”中的“较大数”相当于“部总关系”的“总数”，“相差关系”的“较小数”和“相差数”相当于“部总关系”的两个“部分数”。如下图：

（四）精心设计，探索课堂模型

数量关系的渗透还可以扩大到计算领域——填空式计算，如何把“部总关系”的渗透教学应用到填空式计算领域呢？笔者认为可以从以下两个方面展开：

1. 画一画，沟通算式与部总关系的联系

笔者在教学人教版一年级上册第24页《加法》和第26页《减法》时就第一次构建了“部总关系”的雏形。第81页正式提出加、减法各部分的名称，即“加数+加数=和”和“被减数-减数=差”，这时我们就可以跟“部总关系”进行沟通了——“和”和“被减数”相当于“总数”，“加数”“减数”和“差”相当于“部分数”。如下图：

沟通了算式各部分和“部总关系”的联系，我们就可以解决学生比较容易出错的填空式计算题了。如4+（）=12、9-（）=3、（）-6=7，笔者可以让学生先知道每道题求的是什么，如果求总数，就用加法；如果求部分数就用减法。即：

2. 编一编，加深对部总关系模型的运用

我们还可以让学生根据填空式计算题，编一编数学问题，并让学生判断每道题求的是什么，如果求总数，就用加法；如果求部分数，就用减法。即：

通过编一编的活动，学生能把抽象的填空式计算题转化成形象的计算类解决问题，赋予计算题以生命，同时也促进了学生对“部总关系”的灵活运用。

四、 成效及体会

（一）成效——填空式计算题解题模式的建立

一年来，笔者边教学边研究，探索出了一套运用“部总关系”来解决所有一年级填空式计算题的解题模式，如下图：

第一步，我们需要用“画一画”的方法把原题转变成“部总关系模型图”。

第二步，根据“部总关系模型图”判断题目要我们求的是什么数。这里有两种可能，一种是求总数，另一种是求部分数。

第三步，根据题目求什么来选择加减法。求总数，就要用加法，即用“部分数+部分数”来计算；求部分数，就要用减法，即用“总数-部分数”来计算。

（二）体会

计算教学是基础，但是我们不能一味地用老一套方法枯燥地教学，应该打通各个数学领域，把应用题教学和计算教学有效地“沟通”起来，让“数量关系”也能在计算领域开花结果，使学生的计算更高效。

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［s］.北京：北京师范大学出版社，2022.

［2］王莉.小学生计算能力培养策略［j］.数学学习与研究，2021（6）：81.

［3］黄静.浅议低段数学中计算题的有效教学［j］.神州印象，2018（5）：269.