应用GeoGebra分析粒子在电磁场中的运动

摘   要：GeoGebra 软件功能强大，易于上手，广泛应用于物理教学的可视化研究。将其融入高考综合题中，可以为抽象概念创造具体的物理情境，从而加深学生对物理模型的理解。创新性地提出了利用GeoGebra软件进行物理模型仿真的策略和步骤。基于这些策略，对近两年物理高考试卷中的均匀场问题、综合场问题及复合磁场临界问题等代表性的电磁学问题进行了可视化研究。总结的仿真策略、技巧和方法为教师提供了有益的教学启发，并为核心素养的培养提供了实践经验。

关键词：GeoGebra；带电粒子；轨迹；可视化

中图分类号：G633.7 文献标识码：A     文章编号：1003-6148（2025）3-0085-5

高中物理电磁学部分理论性强、概念抽象，难以制作合适的教具进行演示。学生往往难以形成直观的物理图像，仅靠文字描述和公式介绍显得枯燥，导致学习兴趣低下。此外，该部分题目的设计综合性强且难度较大，对学生的空间想象能力要求较高。带电粒子在磁场中的运动是高中物理必修第三册的热门考点，尤其是带电粒子在有界磁场中运动的临界情况。此外，带电粒子的多解问题和周期性问题等综合性问题也具有较强的开放性。因此，使用仿真软件辅助教学、建构物理模型，对于突破电磁学教学中的重难点显得尤为重要。

目前常用的仿真软件包括ＭＡＴＬＡＢ［１］、Ｍａｔｈｅｍａｔｉｃａ［２］、Ｍａｐｌｅ［３］、ＶＰｙｔｈｏｎ［４］、Ａｌｇｏｄｏｏ和Ｎｏｂｏｏｋ等。其中，ＭＡＴＬＡＢ、Ｍａｔｈｅｍａｔｉｃａ和Ｍａｐｌｅ需要较强的编程基础，学习和创新的门槛较高，不利于推广。Ｖｐｙｔｈｏｎ可以模拟物理动画［５］，作图能力强，但调试代码时较为麻烦。几何画板的脚本功能使用难度较大，物理演示能力有限［６］。Ａｌｇｏｄｏｏ和Ｎｏｂｏｏｋ操作简单，动态力学问题的演示效果很好，但原理较为复杂。虽然各种仿真物理实验室的操作相对简单［７－８］，但创新空间有限，系统预设的参数不便于实时调节，可能无法真实还原实验情境。

相比之下，ＧｅｏＧｅｂｒａ软件功能全面、编程简单、免费开源，对计算机性能要求不高，能够在多平台和网页上直接运行［９］。该软件具有强大的交互性，数据计算准确，能够节约实验数据处理时间，并轻松绘制多维图像，直观展示图像的动态变化效果，实现整个物理过程的可视化。因此，使用ＧｅｏＧｅｂｒａ软件动态展示轨迹辅助教学，分析几何关系和临界条件，有助于学生理解动态变化过程，掌握常见结论并快速找到解题突破口。与常规的板书讲解相比，动画形式更能吸引学生的兴趣，呈现方式更加规范和直观。

1    ＧｅｏＧｅｂｒａ软件仿真的策略

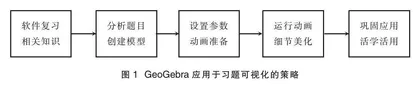
对于教师如何恰当地利用ＧｅｏＧｅｂｒａ进行电磁学习题的仿真，提供了制作课件的思路，并结合案例进行应用。内容包括如何利用指令完成参数设置、动画的绘制和美化等，如图１所示。

（1）复习相关电磁学知识：

①分析几何关系。

②分析运动特征。

（2）剖析题目，建构物理情境：

①绘制几何模型：使用交点工具创建点、线段、坐标系，利用圆形工具设置轨迹圆心和半径。

②设计物理量：使用移动工具进行放缩，添加滑动条以设定可变参数范围。

③设置物理场：根据条件创建电场或磁场，使用虚实度滑动条表示场内部的填充效果。

（3）进行动画设置：

①使用序列设置启动位置，为动画赋予布尔值和时间间隔；创建动点并连接线段，形成圆弧。

②根据题意初始化序列和动画滑动条。

③建立相关力学方程，分析粒子运动。

④根据要求找到需要分析的状态，并标注重要物理量。

（4）动画调试和界面优化：

①使用选框工具设置绘图区，并与滑动条关联，以实现图像移动效果。

②应用显示条件使过程连贯，精心设计交互界面和物理变量构件，注重美化。

（5）巩固模型应用，分析解决策略，达到活学活用。

2    案例研究

2．１    均匀场问题仿真

2．１．１    案例介绍

２０２３年全国甲卷第２０题：光滑绝缘圆筒内存在匀强磁场，筒的Ｐ点开有小孔，过Ｐ的横截面是以Ｏ为圆心的圆，如图２所示。一带电粒子从Ｐ点沿ＰＯ方向射入，并与筒壁发生碰撞。假设粒子在每次碰撞前后瞬间，速度沿圆上碰撞点的切线方向的分量大小不变，沿法线方向的分量大小不变且方向相反；电荷量不变，不计重力。下列说法中，正确的是（      ）

Ａ．粒子的运动轨迹可能通过圆心Ｏ

Ｂ．最少经２次碰撞，粒子就可能从小孔射出

Ｃ．射入小孔时粒子的速度越大，在圆内运动时间越短

Ｄ．每次碰撞后瞬间，粒子速度方向一定平行于碰撞点与圆心Ｏ的连线

2．１．２    案例分析

题目具有一定的创新性和综合性，所考查的知识点也很具代表性。然而，可以进一步拓展，设计一个通用的圆形磁场中粒子偏转情况的模拟程序，使题目更加开放，从而揭示更普遍的运动规律，并归纳出递推结论。该程序可以设置电荷性质和磁场方向的变化，允许拖动调整粒子起点位置，并通过改变速度矢量的大小和方向来观察不同情况下粒子的运动状态，生成多个动画。同时，可以实时展示粒子运动轨迹的切线（速度方向），帮助学生全面理解粒子的运动性质。

对于前三个选项，可以通过改变初速度的大小和方向，观察粒子运动轨迹的动画并分析，从而得出结论：粒子的运动轨迹不可能通过圆心，必须至少经过3次碰撞才能从小孔射出，如图3（a）所示。在改变粒子射入小孔的速度后，可以得到4次、5次和6次碰撞的运动轨迹，分别如图3（b）（c）（d）所示。另外，还可以得到图3（e）所示的多次碰撞轨迹，其相应的运动时间需要结合轨迹分析圆心角的总和。通过程序可以显示圆心并计算圆心角度数，从而得出速度与时间之间并无确定联系的结论。对于Ｄ选项，动画展示了运动轨迹的切线方向，即速度方向，证明碰撞后粒子的速度方向一定位于圆心连线上。

本题易出错的主要原因是学生难以直观理解或作图能力不足，而软件辅助教学可以更精确地揭示几何关系，从而研究圆心角与速度、弦长与速度等的关系，得出定性和定量的结论。

2．２    组合场综合问题仿真

2．２．１    案例介绍

２０２３年湖南卷第６题：如图４所示，区域Ⅰ中存在匀强电场和匀强磁场，电场方向竖直向下，磁场方向垂直纸面向里，等腰直角三角形ＣＧＦ区域（区域Ⅱ）内存在匀强磁场，磁场方向垂直纸面向外。图中Ａ、Ｃ、Ｏ三点在同一直线上，ＡＯ与ＧＦ垂直，且与电场和磁场方向均垂直。Ａ点处的粒子源持续将比荷一定但速率不同的粒子射入区域Ⅰ中，只有沿直线ＡＣ运动的粒子才能进入区域Ⅱ。若区域Ⅰ中电场强度为E、磁感应强度为B1，区域Ⅱ中磁感应强度为B2，则从ＣＦ的中点射出的粒子在区域Ⅱ中运动的时间为t0。若改变电场或磁场强弱，能进入区域Ⅱ中的粒子在区域Ⅱ中运动的时间为t，不计粒子的重力及粒子之间的相互作用，下列说法中正确的是（    ）

Ａ．若仅将区域Ⅰ中磁感应强度大小变为２B1，则t>t0

Ｂ．若仅将区域Ⅰ中电场强度大小变为２E，则t>t0

Ｃ．若仅将区域Ⅱ中磁感应强度大小变为B2，则t=

Ｄ．若仅将区域Ⅱ中磁感应强度大小变为B2，则t=t

2．２．２    案例分析

分析题意可知，区域Ｉ中的复合电磁场起到了速度选择器的作用，只有满足洛伦兹力和电场力平衡的粒子才能沿直线ＡＣ进入区域Ⅱ。如果只改变区域Ｉ的电场或磁感应强度（选项Ａ和Ｂ），则会改变粒子进入区域ＩＩ的初速度，从而改变粒子在区域ＩＩ中进行圆周运动的半径。如果改变区域ＩＩ的磁感应强度（选项Ｃ和Ｄ），则会直接改变粒子在区域ＩＩ中进行圆周运动的半径。无论哪种情况，都可以通过几何关系计算出粒子在区域ＩＩ中的运动时间对应的圆心角。

通过ＧｅｏＧｅｂｒａ软件设置对应的复合场以及三角形磁场，根据题意，调整区域Ⅰ中电场强度E、磁感应强度B1，以及区域Ⅱ中的磁感应强度B2，使粒子从ＣＦ的中点射出。通过模拟动画观察粒子在复合场中的运动轨迹，可以直观地分析出在区域Ⅱ中运动的时间为t0时对应的圆心角为９０°。

对于选项Ａ，将磁场Ｉ的磁感应强度改为原来的两倍，此时粒子的运动轨迹如图５（ａ）所示。通过轨迹分析可知，粒子从ＣＦ的四等分点处竖直向下射出。对于选项Ｂ，将区域Ｉ的电场强度变为原来的两倍，此时粒子的运动轨迹如图５（ｂ）所示，粒子从Ｅ＇点竖直向下射出。根据软件标注，两种情形下粒子在区域ＩＩ中的运动圆心角均为９０°，即运动时间仍为ｔ0。

对于选项Ｃ和Ｄ，改变磁场Ⅱ磁感应强度的大小，粒子的运动轨迹分别如图５（ｃ）（ｄ）所示，对应的圆心角分别为６０°和４５°。通过软件计算可知，改变磁场后粒子在区域 ＩＩ 中的运动时间也发生了变化。清晰的几何图像能为解题提供有益思路，帮助教师突破教学难点，有效提高学生的建模能力和科学思维。此外，在制作课件时，可以注重动画色彩的搭配和辅助线的使用，以增强直观性和严谨性。

2．３    复合磁场临界问题仿真

2．３．１    案例介绍

２０２３年浙江卷第20题：如图６所示，ｘＯｙ平面的第一象限内有足够长且宽均为L、边界均平行x轴的两个区域，其中区域Ⅰ存在磁感应强度大小为B1的匀强磁场，区域Ⅱ存在磁感应强度大小为B2的磁场，方向均垂直纸面向里，区域Ⅱ的下边界与x轴重合。位于（０，3L）处的离子源能释放出质量为m、电荷量为q、速度方向与x轴夹角为６０°的正离子束，沿纸面射向磁场区域。不计离子的重力及相互作用，并忽略边界效应。

（１）求离子不进入区域Ⅱ的最大速度v1及其在磁场中的运动时间t。

（２）若B2=2B1，求能到达y=处的离子的最小速度v2。

2．３．２    案例分析

对于第（１）小问，根据离子在磁场中运动的规律，需要找到离子恰好不进入区域Ⅱ的最大速度v1。可以在ＧｅｏＧｅｂｒａ软件中分段设置磁场条件，改变离子运动的速度，以找到图７（ａ）中运动轨迹与磁场Ⅰ边界相切的情况。在代数区设置显示圆心，此时轨迹的圆心是B'1，并可以动态展示圆心角的变化，精准标明角度大小，实时计算出运动时间t。

对于第（２）小问，改变磁场条件，使得B2=2B1。能够到达y=处的离子的临界条件应该与直线y=相切，在磁场Ⅰ和Ⅱ中的运动轨迹如图７（ｂ）所示。可采用以下三种方法解题：

①几何解法：计算运动半径、离子速度，并利用正弦定理求出角度和边的关系。

②比例关系法：根据B2=2B1，得出离子在磁场ＩＩ中运动半径是磁场Ｉ中的，联立可求出临界速度。

③等效思想法：B2=2B1时，离子运动到y=处，等效于在B2=B1时，离子恰好运动到y=0处，轨迹如图7（c）所示，根据仿真得到的几何关系即可求出速度v2。

通过仿真，可以精确找到临界条件，并通过角度变化加深对整个运动过程的理解。可以添加轨迹圆心的追踪效果，方便观察运动情况，在使用位似工具之前要先建立好交点。在制作课件时，可建立滑动条之间的联系，简化界面，以找到滑动条计数与轨迹的对应关系。

3    建议与小结

三个案例解题的关键在于找到确切的几何关系。这类涉及思维抽象和动态变化的问题，可以利用软件仿真将粒子运动可视化。生动直观的图像比概括性文字更有助于学生理解物理概念，避免思维误区，并激发他们的探究兴趣，具有很强的启发性。这种教学模式也易于推广。

近年来，三维空间情境中的物理问题变得非常常见，对学生的空间想象能力要求也更高。教师可以考虑通过相应的仿真，将问题分割和简化。例如，２０２４年湖南卷中粒子在圆筒中的运动问题，２０２２年全国乙卷中经典的Ｐｈｙｐｈｏｘ地磁场测量问题，以及２０２２年重庆卷中“全超导托卡马克核聚变实验装置的约束问题”。利用软件建立三维模型中的运动轨迹，能够更高效地突破难点，并更好地体现可视化程序开发的优越性。

参考文献：

［１］姚瑞锐，李丰果． ＭＡＴＬＡＢ在高中物理教学中的应用研究综述［Ｊ］．物理通报，２０２２（１２）：１４３－１４７．

［２］吴玉辉，梁永军，范争丽． 使用Ｍａｔｈｍａｔｉｃａ软件绘制原子轨道［Ｊ］．科技视界，２０１７（１４）：９６，４４．

［３］孟勇．利用Ｍａｐｌｅ软件分析带电粒子在磁场中的运动——以三类动态圆问题为例［Ｊ］．物理之友，２０２３，３９（１）：５９－６２．

［４］梁见斌．Ｐｙｔｈｏｎ编程作图物理仿真项目进阶设计——从落体小球到漫天烟花［Ｊ］．中国信息技术教育，２０２１（７）：２８－３０．

［５］王瑶，刘玉颖，朱世秋．静电场及电荷运动的ＶＰｙｔｈｏｎ可视化模拟［Ｊ］．大学物理，２０２０，３９（９）：７２－７７．

［６］王前锋．几何画板融入高中物理教学的教学设计案例研究［Ｄ］．重庆：重庆师范大学，２０２３．

［７］韦情枫．基于虚拟仿真的高中物理情景可视化研究［Ｄ］．南宁：广西师范大学，２０２２．

［８］王志鹏．虚拟仿真实验在高中物理教学中的应用研究［Ｄ］．重庆：西南大学，２０２３．

［９］金惠吉，王静． ＧｅｏＧｅｂｒａ软件在物理教学中的应用研究综述［Ｊ］．物理通报，２０２１（６）：１４５－１４８．

（栏目编辑    贾伟尧）

收稿日期：2024-09-01

基金项目：四川省教育信息技术研究项目“基于中华传统科技文化的初中STEAM校本课程建设”（DSJZXKT023）；济源市基础教育教学研究项目“高中物理教学中情境创设的实践研究”（JY240656）。

作者简介：邓欣（2002-），女，中学二级教师，主要从事高中物理教学研究。