发展学生模型意识的有效策略

［摘 要］模型意识是数学核心素养的重要组成部分，学生需要具备并发展模型意识，为持续学习提供思想支持。要发展学生的模型意识，教师应该扎根课堂教学，逐步渗透模型意识。文章以苏教版教材“解决问题的策略（转化）”一课为例，阐述发展模型意识的有效策略：深挖故事，孕伏模型的结构；分层推进，构建模型的脉络；转换视角，把握模型的本质；丰富变式，拓宽模型的外延；联结沟通，体会模型的价值。

［关键词］转化；模型意识；解决问题

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）08-0075-04

模型意识有助于增强学生对数学的应用意识，让学生体会数学的应用价值，认识到模型可以解决一类问题。发展模型意识，要结合学生的认知水平，由浅入深、循序渐进地进行教学。本节课的教学贴近学生的需求，运用有效策略帮助学生感悟模型的本质特点。

一、深挖故事，孕伏模型的结构

数学模型的构建是基于对情境的抽象和对问题的表征。因此，教师要深挖故事，提出有代表性的问题，孕伏模型的结构，从而激发学生建模的兴趣，让学生感悟模型的结构，为下一步构建模型打下基础。

师：你们听过“曹冲称象”的故事吗？他是怎样称出大象的质量的？我们一起来看一下。

（教师播放《曹冲称象》动画）

师：为什么要把大象换成石头？

生1：如果直接称大象，就要造一杆很大的秤，很麻烦。

师：当我们遇到复杂的问题时，就要想办法把它转化成一个简单的问题。那为什么称出了石头的质量就能知道大象的质量？

生2：石头和大象都能把船往水里压，压到一样的程度，互相转化后，它们的质量是一样的。

师：是的，转化过程中质量是不变的。今天我们就一起来学习这个解决问题的策略——转化。

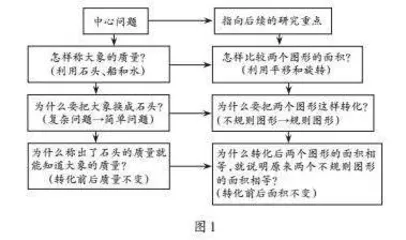
在这一教学环节中，教师提出三个关键问题：怎样称大象的质量？为什么要把大象换成石头？为什么称出了石头的质量就能知道大象的质量？这三个问题层层深入，孕伏后续的模型内涵。教师设计这三个问题的意图如图1所示。

三个关键问题使得学生深刻理解故事背后的道理，自然而然地思考转化的意义，让学生初步感悟转化模型，激发学生的学习兴趣和求知欲。

二、分层推进，构建模型的脉络

想让学生摸清模型的脉络，教师就要站在学生的角度上考虑，将资源进行分类，有序推进，搭建符合学生认知发展规律的交流平台。只有通过丰富的资源对比，才能让学生多维度感知事物的特征，帮助他们抓住模型的本质，构建模型的脉络。对此，笔者设计了以下教学环节。

师：大家欣赏谁的做法？

生3：我欣赏生2的做法，因为比较简便。

师：生2的做法有什么特点？

生4：把不规则图形转化成了规则图形。

师：为什么转化后的两个长方形的面积相等，就能说明转化前的两个不规则图形的面积相等呢？

生5：转化前后图形的面积没有发生变化。

师：是的，可以在变化中找到不变的量。

此教学环节，学生的做法有两种，分别是数格子的方法和转化方法。教师引导学生对比不同的方法，并用“为什么转化后的长方形的面积相等，就能说明转化前的不规则图形面积相等？”这一问题带领学生明确等积变换的本质——转化前后图形的面积没有发生变化。教师要将问题抽丝剥茧，才能帮助学生触摸数学知识的本质，构建模型的脉络和结构。

三、转换视角，把握模型的本质

构建模型不能局限于一个视角，要从不同的视角找到知识的本质，从而构建相应的模型。学生在经历探究并构建模型后，教师应为学生提供丰富的练习，帮助学生体会许多数学问题本质上都是指向同一个模型。

就这节课而言，等积变换模型是教学的重难点。在转化时，可以将图形本身进行转化，也可以将图形外的空白部分进行转化，但这两种方法归根到底都是将“面”进行平移或旋转。教师应该让学生体会到这一点，从多个视角感悟等积变换的内涵。对此，笔者设计了以下教学环节。

师：比较图4中直条面积的大小。（长方形面积相等，直条宽度相等）

生1：把左边图形的直条图案分别平移到边上，就跟右边图形的直条图案是一样的了。

师：比较图5中各图形阴影部分面积的大小。（长方形面积相等，直条宽度相等）

生2：①号图形的阴影部分与②号图形的阴影部分等底等高，面积相等。

生3：计算③号图形的阴影部分的面积用不了面积公式，比较起来有困难。

师：没关系，我带来了这三个图案的模型，请你仔细观察③号图形左边空白部分和右边空白部分的形状，你有什么想说的？

生4（边操作边说，如图6）：可以把左边的空白部分向右侧移动，与右边的空白部分拼在一起。

师：大家还想再看一遍吗？请生4再演示一遍。但这次我有个要求，请大家仔细观察，原来的“S”形图案转化后“跑”去哪里了？

（生4再次操作）

生5：“S”型图案转化成了左端的小长方形，转化后，可以看出③号图形阴影部分的面积与①号图形阴影部分的面积相等。

师：照这样的思路，谁来转化①号图形和②号图形的空白部分？

（生6上台操作，如图7-1、图7-2）

生6：它们的空白部分都可以通过平移，转化成相同的长方形，因此①号图形、②号图形、③号图形阴影部分的面积是相等的。

师：回顾刚才做的这两道题，它们有什么相同点和不同点？

生7：相同点是这两题都是将面进行平移。不同点是第一题我们直接比图案，第二题我们比了空白部分。

师：当我们在比较面积时，除了可以直接转化图案本身，还可以转化空白部分。但无论哪种方法，本质上都是将面进行平移。

以上教学环节包含两道题：第一题是对阴影部分进行等积变换，第二题是对空白部分进行等积变换。学生发现，图5中③号图形的阴影部分很难直接比较，以此产生认知冲突。为此，教师组织三次操作活动：第一次，聚焦空白部分，明确③号图形的空白部分能够转化成一个长方形；第二次，聚焦阴影部分，使学生发现阴影部分转化成了左端的小长方形；第三次，聚焦①号图形和②号图形，将它们的空白部分进行变换，再次巩固转化策略。学生在活动中感悟，如果直接比较阴影部分的面积行不通，可以转换视角，将空白部分进行转化。但不论是哪种方式，本质都是对面的平移。

四、丰富变式，拓宽模型的外延

除了在不同的问题中找到相同的本质，抽象出相同的数学模型，还可以改变情境中的关键量，探究关键量与结果的关系，从而拓宽模型的外延，培养学生的模型意识。就这节课而言，除了上文提到的等积变换模型，等长变换模型也是重点。这两种变换有相同点，也有不同点，教师可以通过丰富的变式练习让学生深刻地理解等积变换模型和等长变换模型。对此，教师设计了以下教学环节。

师：求图8中右边图形的周长，每小格的边长是1厘米。

师：这两种解法，哪一种正确？

生1：第一种解法正确。

生2：第二种解法是转化面，而这题求的是周长。

师：做完这道题，你想提醒大家什么？

生3：解题时一定要先看清是求面积还是求周长，再转化。

师：到现在为止，我们解决了许多题，如果要你把这几道题分类，你会怎样分？

生4：分成两类，前几题都是转化前后图形的面积不变，最后一题是转化前后图形的周长不变。

师：没错。转化前后图形的面积不变，在数学上叫等积变换。转化前后图形的周长不变，在数学上叫等长变换。

师（出示图10）：下图中左边图形的面积和右边哪个图形的面积相等？左边图形的周长和右边哪个图形的周长相等？

生5：将左边图形的小半圆补到空白部分，左边图形的面积就和①号图形的面积相等。将左边图形两条短的弧转化成一条长的弧，左边图形的周长就和②号图形的周长相等。

师：你觉得等积变换和等长变换有什么相同点和不同点呢？

生6：相同点是图形转化过程中都有一个量保持不变。

生7：不同点是等积变换是转化前后图形的面积不变，等长变换是转化前后图形的周长不变。

以上教学环节涉及两个问题。第一个问题旨在让学生认识等长变换，先将正确的解法和错误的解法进行对比，再将前面做过的题目放在一起对比并总结。第二个问题不仅涉及圆的周长和面积的知识，还将等积变换模型与等长变换模型放在一起，要求学生独立辨认，这是对学生综合能力的考查。丰富的变式使得学生在对比和交流中，深刻地认识到这两类模型的特点，发展模型意识，激发学习数学的兴趣。

五、联结沟通，体会模型的价值

吕林海教授认为，学会数学学习的“会”有两种含义，一是“工具性的三会”；二是“本质性的三会”。从学会使用工具转向学会认识本质，才是发展数学核心素养的关键。就“转化”这节课而言，不能只教学解题策略和数学模型，还要将转化策略与生活联系起来。只有这样，学生才能在掌握知识的同时内化转化策略，感悟模型的价值。具体的教学环节如下。

师：大家谈谈今天的收获。

生1：我学会了等积变换和等长变换。

生2：我知道了转化能让问题更简单。

师：没错，转化是数学中十分重要的策略。转化不仅存在于数学中，在生活中也有它的身影。课堂的最后，我请大家看一个小故事（如图11）。

师：你看懂这个故事了吗？你有什么想说的？

生3：我看懂了，实际上人们都是花了100元买了一只鸡。

生4：这个老板真聪明啊。

师：老板转换营销策略，成功将养鸡场里的鸡都卖出去了，这就是老板的智慧。希望同学们不仅能在数学中用转化策略解决数学问题，还能在生活中利用转化策略解决实际问题。

通过以上教学环节，学生深刻认识到转化的价值：它既可以帮我们解决数学问题，也可以帮我们解决生活中的困难。

转化不仅限于等积变换和等长变换，也不仅限于数学这门学科。转化是一种思想，可以跨越多门学科，也与生活紧密相连，它是一种智慧的策略。

综上所述，教师要从实际情况出发，开展课堂教学，探寻有效策略，让学生参与模型的构建与运用，帮助学生感悟模型的本质，体会模型的价值，厘清模型的脉络并将其运用于生活中，使得学生的模型意识落地生根。

［ 参 考 文 献 ］

[1] 孙保华.发展模型意识的有效策略[J].小学数学教育，2023（10）：14-16.

[2] 吕林海.“三会”，应超越工具性而存在[J].教育视界，2023（6）：1.

（责编    黄    露）