基于单元整体视角的小学数学练习课堂优化设计

【摘 要】本文分析了基于单元整体的小学数学练习课堂的设计要点，以及围绕单元整体教学的背景下如何优化设计小学数学练习课堂提出了几点策略，以期为相关人员提供参考。

【关键词】练习课堂 单元整体 关联 整合

练习课堂是小学数学教学中的重要环节，学生在完成练习任务的过程中，能够巩固所学的新知识，并建立新知识与旧知识之间的联系，以此提升学生的数学技能与能力。在单元整体的教学背景下，教师应将单元概念融入练习课堂的设计中，整合单元课程的相关知识点，提升练习课堂的教学成效。

一、明确针对性内容，实现深度思考

基于单元整体的数学练习课堂中，教师应设计具有针对性的练习内容，依据学生的学习水平设计有效的练习任务，提升、强化学生的数学知识与数学技能。教师要在确定练习课堂的主题后，选出符合要求的练习内容，可以改编教材中的例题、练习题，也可以依据学生的发展需求原创练习内容，使基于单元整体的课堂练习更具针对性，从而提升学生的思维能力。

以苏教版六下“圆柱和圆锥”单元为例，教师依据本单元围绕定性研究与定量研究两个维度设计教学内容：（1）引导学生学会求解圆柱与圆锥的表面积和体积；（2）引导学生了解旋转体的特征。教师可以结合单元教学内容设计以圆柱和圆锥体积关系为主题的针对性练习活动，设计基础题、延伸题、拓展题三个层次的练习。其中，包括同底等高的圆柱和圆锥体积关系的基础练习；同底等体积（或等高等体积）圆柱和圆锥高的关系（或底面积关系）的延伸练习；既不等底也不等高圆柱和圆锥的体积变化关系。同时，将比的知识结合到练习中，引导学生求解，由此培养学生的空间观念与模型意识。

环节一：出示圆柱和圆锥（标有底面积和高）。学生依据给出的信息，分别求出圆柱和圆锥的体积，再说两者体积关系。环节二：变换题目条件及问题信息，圆柱和圆锥的高相等，体积都是90π cm3，再给出圆柱底面积为36π cm2，求圆锥的底面积是多少？环节三：再次变换练习问题与条件，圆柱和圆锥的底面半径比是1∶2，体积相等是90π cm3，两者高的比是几比几？

借助此类变换的练习内容，引导学生探究圆锥与圆柱体积之间的关系，加深学生对本单元内容的理解，进而从不同的角度体验数学知识的应用，提升学生的数学技能。

二、关联数学知识，发散学生思维

基于单元整体的小学数学练习课堂设计，要求教师挖掘教材中与该单元相关的知识线索以及蕴含的数学方法。转变传统练习课堂中内容单一、信息组织零散等缺陷，帮助学生建立知识之间的联系。在发散学生数学思维的同时，促使学生掌握数学知识的本质，并学会应用数学方法，进而提升学生的数学学习能力。

例如，在苏教版五下“圆”这一单元中，教师可以设计渗透圆面积推导过程的相关练习。

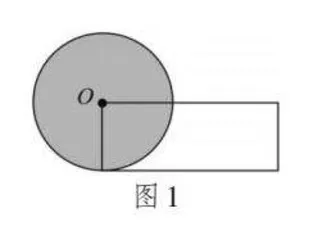
如图1，长方形和圆的面积相等，它们的周长对比后可知（ ）。

A.圆的周长小于长方形的周长

B.圆的周长大于长方形的周长

C.圆的周长等于长方形的周长

D.无法确定哪个更长

教师可以借助课前准备好的学具引导学生思考如何利用圆的面积推导过程启发学生思考。使学生在联系圆面积的推导过程中厘清圆周长和长方形周长的关系。借助此类关联数学知识的练习课堂，学生在解决问题过程中梳理知识脉络，以培养他们的数学发散思维、逻辑思维。

三、聚焦综合活动，加强知识认知

从教育心理学的视角来看，小学阶段是儿童认知发展的关键时期，学生正逐步从形象思维向抽象思维过渡，而综合活动恰能为这一过渡搭建稳固的桥梁。在练习课堂中，教师须依据新课标，深度剖析教材知识体系，精准洞察学生现有的认知水平、知识储备以及学习能力的差异。教师明确练习课堂应达到的目标，巧妙融合趣味性、挑战性与教育性，充分考虑如何激发学生的内在学习动机设计练习，进而在练习活动中实现数学思维的培养，推动学生突破思维定式，提升学生对数学知识的综合运用能力。

例如，在苏教版三上“正方形和长方形”单元与周长相关的课堂教学中，教师发现学生在面对灵活多变的问题时，往往存在思维固化的情况。此时，教师就要设计综合练习活动，加深学生对数学知识的认知，同时也帮助他们突破思维定式、发散数学思维。因此，教师在练习课堂中设计综合活动引导学生深入对知识的认知。

活动一：教师提供20个边长为1 cm的小正方形纸片。（1）用20个小正方形纸片拼出周长最短的长方形，并探究该长方形的长和宽分别为多少厘米？（2）用20个小正方形纸片拼出周长最长的长方形，并探究长方形的长和宽分别为多少厘米？活动二：如果用9根长1 cm的小棒围长方形，有几种围法？并用画图表示。

在活动中，教师引导学生动手操作，从实践中比较长方形与正方形之间的差异，进而加深对长方形、正方形周长的认知，提升练习课堂的效果。

四、紧扣单元目标，凸显单元整合

在单元整体的宏观视野下，小学数学单元目标的制定至关重要，它要求教师积极转变传统教学模式，深度钻研并灵活运用数学教材，充分挖掘其中蕴含的课程编排意图，为细致入微地剖析课时内容和单元整合做准备。这要求教师不仅要敏锐洞察数学知识之间千丝万缕的关联性，更要精心思索采用何种巧妙的教学方式，将这些看似零散实则紧密相连的知识，以一种有机融合的方式呈现给学生。

以苏教版四下“三位数乘两位数”为例，依据本单元教材的基本结构确定本单元的教学目标：（1）理解和掌握三位数乘两位数的笔算方法，用简便方法笔算乘数末尾有0的乘法。（2）理解积的变化规律，懂得应用积的变化规律口算几百乘几十。（3）能够应用常见的数量关系解决实际问题，并掌握、应用与单价、数量有关的常见数量关系。根据上述单元目标，设计以下的单元练习。

1. 图2中（ ）点表示的数可能是5 □ 9 × 55的积？

2. 有一个宽为12米的长方形，面积是192平方米。如果宽增加12米，要使面积不变，原来的长要（ ）。

A. 减少12米    B. 扩大2倍     C. 缩小2倍      D. 增加12米

3. 下面的问题中，不能用218×20这个算式来解决的是（ ）。

A. 一种足球运动服的单价是218元／套，学校买了20套这样的运动服，一共要付多少元？

B. 陈老师骑车的平均速度是218米／分，她骑20分钟一共骑行多少米？

C. 长方形的长是218米，宽20米，面积是多少平方米？

D. 妙想20天看了218页书，平均每天看多少页？

诸如以上这些设计，应依据单元教学目标的达成情况，以串联式题组的方式对整个单元的知识进行整合，呈现具有代表性的题目，将方法与技巧融入其中，助推学生基于单元教学的深入学习，让学生通过练习发现各个习题所蕴含的知识及数学方法，以此对整个单元的知识内容及思维方法进行有效建构，达成深入理解和巩固单元知识的目的。

（作者单位：福建省福安市穆阳中心小学）

参考文献

［1］蓝艺明.小学数学主题式练习课：基本内涵、设计原则与教学实践［J］.教育科学论坛，2023 （35）：43-47.

［2］杨丽琴.小学数学练习设计的优化策略［J］.亚太教育，2021 （22）：119-120.