“三点两面五步定位法”绘制太阳周日视运动轨迹

［摘 要］运用“三点两面五步定位法”能够快速准确地绘制太阳周日视运动轨迹，提高学生对太阳周日视运动规律的认识。在此方法中，“三点”指“三点定位”，是太阳周日视运动轨迹中三个重要坐标点的空间方位，它们分别是正午太阳方位、日出方位和日落方位。“两面”分别指观察点当日的太阳视运动轨迹面和二分日的太阳视运动轨迹面（春分日和秋分日）。“五步”指的是完成绘图的五个操作步骤：第一步，计算观察点的正午太阳高度；第二步，确定正午太阳在地平面上的水平方位；第三步，确定日出方位和日落方位；第四步，确定太阳视运动轨迹面的倾斜方向；第五步，用当地的二分日的太阳视运动轨迹面作为参考，检查正误。文章最后以观察点φ=10°N，直射点δ=20°N为例，详细描述了运用“三点两面五步定位法”绘制太阳周日视运动轨迹的操作步骤。

［关键词］太阳；周日视运动；轨迹；绘制方法

［中图分类号］    G633.55               ［文献标识码］    A                ［文章编号］    1674-6058（2025）07-0078-05

太阳周日视运动轨迹的绘制一直是高中地理教学中的难点，这个难点体现在多个方面。一是知识点的理解难度大，天体的运动规律本身就是相对抽象的概念，现象也复杂多变。二是学生的学习难度大，部分学生逻辑思维能力欠缺，对于视运动的绘制总是陷入生搬硬套的怪圈。三是教师教学的难度大，部分教师对周日视运动的理解模糊不清，或者对视运动轨迹的绘制方法归纳没有形成体系，在教学过程中总结模糊，学生听得云里雾里。

因为太阳周日视运动轨迹这一知识点对学生地理核心素养的考查较为全面，比如涉及综合思维、地理实践力和区域认知的考查，体现地理学科的综合性和区域性两个特点，所以在高中地理试题中的考查频率越来越高，难度也有所提升。这就对教师总结绘制太阳周日视运动轨迹的方法提出了更高的要求。本文将太阳周日视运动轨迹的绘制方法总结为“三点两面五步定位法”，接下来对此方法进行原理阐述并运用实例展示。

一、“三点两面五步定位法”的概念

（一）“三点”的含义

“三点”指“三点定位”，即通过三个点来确定在假想的天球空间中地平面以上的太阳周日视运动轨迹形成的平面（以下论述中统一称为“太阳视运动轨迹面”）。这三个点指的是三个参考点的空间方位，它们分别是正午太阳方位、日出方位和日落方位。其中，正午太阳方位比较特殊，需要结合观察点当日的正午太阳高度和正午太阳在地平面上的水平方位共同确定。

（二）“两面”的含义

“两面”中的“一面”指的是太阳视运动轨迹面（及其在空间内的倾斜状况）。通过“三点定位”虽然能够形成一个太阳视运动轨迹面，但是太阳视运动轨迹面在空间内的倾斜状况很难判断，而这是绘制太阳周日视运动轨迹的重中之重。太阳视运动轨迹面是朝南天空倾斜还是朝北天空倾斜，这是正确绘制太阳视运动轨迹的关键。接下来笔者会对此进行重点说明。“两面”中的“另一面”指的是二分日（春分日和秋分日）的太阳视运动轨迹面。受日地距离、地球直径等因素的影响，如果我们将太阳光线看作近似相互平行的光线，那么任何一天的太阳视运动轨迹面之间必定是相互平行的，所以，一年中任何一天的太阳视运动轨迹面必定与二分日的太阳视运动轨迹面相互平行。可以运用这一规律，将其作为检查绘制的太阳周日视运动轨迹是否正确的重要法宝。

（三）“五步”的含义

“五步”指的是运用此方法绘图的5个重要操作步骤。这5个步骤分别是：1.计算正午太阳高度；2.确定正午太阳在地平面上的水平方位；3.确定日出方位和日落方位；4.确定太阳视运动轨迹面的倾斜方向；5.用二分日的太阳视运动轨迹面作为参考，检查两个轨迹面之间是否相互平行。

二、“三点两面五步定位法”的原理

（一）计算正午太阳高度

正午太阳高度的计算非常简单，可以运用最简单的计算公式：H正午=90°-|纬度差|（观察点与直射点的纬度数值之差，二者位于同半球则数值相减，位于异半球则数值相加）。

（二）确定正午太阳在地平面上的水平方位

如果观察点正当正午时刻（地方时12时），那么此时太阳高度达到一天中最大。观察点任何一日的昼长都是以地方时12时为对称。同样地，地平面以上的太阳视运动轨迹也可以看作是以地方时12时的太阳方位为对称的。所以，我们看到的正午太阳在地平面上的水平方位，不是在正南方位，就是在正北方位。那接下来的关键就是判断正午太阳在地平面上的水平方位什么时候在正南，什么时候在正北。

相信大家在实际生活中都有这样的经验：物体影子的朝向与光源的方位相反。例如，通过立杆见影的方法，观察正午时刻的杆影朝向，与之相反的方位就是正午太阳在地平面上的水平方位。因为杆影的形成是太阳光线照射的结果。那我们来思考这样一个问题：杆子立于地平面上的杆影朝向会受到什么因素的影响？在北半球中纬度的人可以观察到在一年中任何一天的地方时12时，杆影都朝向正北；在北半球低纬度的一些人可以观察到在一年中的某一天地方时12时，杆影朝向正北；但是有些人却说杆影有时朝向正南。为什么会出现这样的差别？这是受到了什么因素的影响？

我们结合前面观察到的现象思考：观察点纬度的不同，会导致杆影朝向出现差异，而同时，一年中太阳直射点也在南北回归线之间做回归运动。这就产生了一个猜想：杆影的朝向是否取决于观察点和直射点之间的相对位置关系？另外，杆影的朝向可以反映正午太阳在地平面上的水平方位，也就是说，正午太阳在地平面上的水平方位是否取决于观察点和直射点之间的相对位置关系？

为了验证这个猜想，我们以观察点φ在北半球为例，结合直射点δ的回归运动（23.5°N≤δ≤23.5°S），分四种假设条件进行验证。假设一为观察点φ在赤道上；假设二为观察点φ在赤道与北回归线之间（0°＜φ＜23.5°N）；假设三为观察点φ在北回归线上；假设四为观察点φ在北回归线以北的地区（φ＞23.5°N）。在进行模拟实验时，因为假设三和假设四中观察点与直射点的相对位置关系会重复出现在假设一和假设二中，所以只需要对假设一和假设二进行讨论与验证即可。

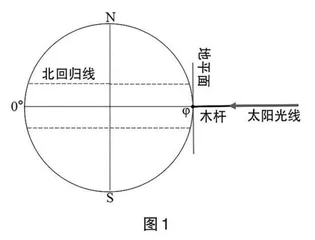
假设一：观察点φ在赤道上，直射点δ纬度范围为23.5°N≤δ≤23.5°S。

①直射点δ纬度=观察点φ纬度，见图1。

结论：无杆影，因为此时太阳位于天顶。

②直射点δ纬度＞观察点φ纬度，直射点在南半球，见图2。

结论：杆影朝北，因为此时太阳位于正南方天空。

③直射点δ纬度＞观察点φ纬度，直射点在北半球，见图3。

结论：杆影朝南，因为此时太阳位于正北方天空。

假设二：观察点φ在赤道与北回归线之间（0°＜φ＜23.5°N），直射点δ纬度范围为23.5°N≤δ≤23.5°S。

①直射点δ纬度=观察点φ纬度，见图4。

结论：无杆影，因为此时太阳位于天顶。

②直射点δ纬度＜观察点φ纬度，见图5。

结论：杆影朝北，因为此时太阳位于正南方天空。

③直射点δ纬度＞观察点φ纬度，见图6。

结论：杆影朝南，因为此时太阳位于正北方天空。

结合假设一和假设二的结论，得到一个重要的认识：正午太阳在地平面上的水平方位，只取决于直射点δ相对于观察点φ的南北位置关系，具体可以分为下列三种情况：

情况一：直射点δ纬度与观察点φ纬度相同时，正午太阳位于天顶；

情况二：直射点δ位于观察点φ以北时，正午太阳位于地平面上的正北方位；

情况三：直射点δ位于观察点φ以南时，正午太阳位于地平面上的正南方位。

（三）确定日出方位和日落方位

情况1：太阳直射赤道，见图7、图8。

结论1：

晨线和经线重合，纬线和太阳光线平行；

太阳在晨线正东方，在昏线的正西方；

故全球（除极点）太阳日出方位为正东，日落方位为正西。

情况2：太阳直射北半球，见图9、图10。

结论2：

晨线和经线不重合，纬线和太阳光线不平行；

太阳在晨线东北方，在昏线的西北方；

故全球（除极昼极夜地区）太阳日出方位为东北，日落方位为西北。

情况3：太阳直射南半球，见图11、图12。

结论3：

晨线和经线不重合，纬线和太阳光线不平行；

太阳在晨线东南方，在昏线的西南方；

故全球（除极昼极夜地区） 太阳日出方位为东南，日落方位为西南。

（四）确定太阳视运动轨迹面的倾斜方向

为了更好地模拟在地平面上观测到的太阳视运动轨迹，我们假设地球是一个无限小的不运动的质点，太阳绕着地球做自东向西的圆周运动。

接下来，假设观察点φ为地球上北半球中纬度的任意点。在假设的天球中，A点为地球，BC所在平面为观察点φ的地平面（因为地球无限小，所以观察点φ可以看成A点），P点为天顶（如图13所示）。为了更贴近日常的观察视角，便于准确观测地平面以上的太阳视运动轨迹，我们将天球进行旋转，使得天顶P朝上（如图14所示）。

我们在图14中可以发现，当假设观察点φ为地球上北半球中纬度的任意点，天顶朝上，地平面旋转至水平时，就是我们日常观察视角下看到的二分二至日太阳视运动轨迹，此时地平面以上的二分二至日太阳视运动轨迹面向南方天空倾斜。那么，就产生了这样一个猜想：观察点的纬度是否影响地平面以上的二分二至日太阳视运动轨迹面的倾斜方向？（在下文中，“地平面以上的二分二至日太阳视运动轨迹面的倾斜方向”统一表述为“二分二至日的太阳视运动轨迹面倾斜方向”）

接下来，我们进行一系列的假设验证这一猜想是否正确。为了让示意图更加清晰明了，我们对天球上的各要素进行简化表示。图15、图16中N和S分别表示天北极和天南极，N点与S点的连线（虚线）表示天轴（也可以看作地轴），N处的四角星即表示北极星，A点表示观察点φ，P点表示观察点的天顶，BC为观察点的地平面，三条线表示该观察点的二分二至日太阳视运动轨迹。

从图15、图16中可以发现：天轴（地轴）与二分二至日太阳视运动轨迹始终保持相互垂直的关系，二分二至日太阳视运动轨迹向南方天空倾斜。

结论一：观察点φ位于北半球中纬度时，二分二至日太阳视运动轨迹面向南方天空倾斜。

（2）假设二：观察点φ为北半球低纬度的任意点，见图17、图18。

从图17、图18中可以发现：天轴（地轴）与二分二至日太阳视运动轨迹始终保持相互垂直的关系，二分二至日太阳视运动轨迹向南方天空倾斜。

结论二：观察点φ位于北半球低纬度时，二分二至日太阳视运动轨迹面向南方天空倾斜。

（3）假设三：观察点φ为北半球高纬度的任意点，见图19、图20。

从图19、图20中可以发现：天轴（地轴）与二分二至日太阳视运动轨迹始终保持相互垂直的关系，二分二至日太阳视运动轨迹面向南方天空倾斜。

结论三：观察点φ位于北半球高纬度时，二分二至日的太阳视运动轨迹面向南方天空倾斜。

（4）假设四：观察点φ为赤道上的某点，见图21、图22。

从图21、图22中可以发现：天轴（地轴）与二分二至日太阳视运动轨迹始终保持相互垂直的关系，二分二至日太阳视运动轨迹与地平面（此时与天轴重合）相互垂直，不倾斜。