引入数学游戏培养小学生推理能力的教学研究

【摘要】立足于“树德育人”的目标，小学数学教育不能停留在“会计算、会解题”的低端要求，而是要通过教学实践帮助学生提高解决数学问题的能力，优化其数学思维。文章探讨在数学课堂引入数学游戏的教学策略，认为数学游戏是教材资源的有益补充，通过设计情境化的灵活的数学问题，让学生在解析过程中训练数据分析、归纳推理等逻辑思维能力，培养严谨审慎的科学精神，有助于数学核心素养和数学思想的形成与发展。

【关键词】小学数学；推理能力；数学游戏；教学策略

【课题项目】本文是福建省三明市基础教育科学研究2023年度立项课题“发展小学生数学归纳推理意识的实践研究”（立项编号：JYKT-23091）的研究成果。

【中图分类号】G623.5   【文献标识码】A 【文章编号】2095-3089（2025）05-0004-03

随着学习进程的深入，数学知识越发深奥与抽象，虽然有的学生感觉学习较为轻松，卷面成绩也养眼，但不可否认，相对于其他学科，其在学习过程中投入了更多的心智与脑力——这不是凭个人意志和喜好可以改变的事实；但更多的学生也付出了大量的时间，仍然感觉学习吃力，难度太大，谈“数”色变，甚至产生抵触、厌烦、恐惧的心理，学习效果不佳。

党的十八大提出“教育要培养受教育者各学科核心素养”的理念，这是比素质教育理念更宏观、更高远的战略目标。《义务教育数学课程标准（2022年版）》（以下简称《新课标》）指出：“数学教育的目标是通过数学学习，学生能够了解数学的价值，提高学习数学的爱好，增加学好数学的信念，养成良好的学习习惯，具有初步的判断意识和实事求是的科学看法。”[1]实现这个目标，需要教育工作者，特别是一线教师，付出更多的努力：努力更新观念，努力改变教学方法，努力服务好学生提高他们的综合素养。具体到小学数学，教师要摒弃“会计算，会解题”这样低端的要求，从学生个人发展的角度，从为国家培养人才的角度出发，采取符合学生实情的教学手段，切实提高学生的数学抽象、逻辑推理、数据分析等学科素养，在课堂引入数学游戏是创新教学方法的大胆尝试。

一、引入数学游戏的背景及其概念与运用价值

数学核心素养之一的“逻辑推理”包括类比推理、归纳推理和演绎推理三种形式（本文统称为推理），是由已知条件推导出结论的思维方式与思维过程，这一过程不是凭空的臆想与猜测，而是要基于事实与事理的一般规律，基于理论知识与生活经验的积累，对事件的走向（或结果）的预知与判断。现阶段小学数学教材的习题，其问题设计的方式直观而透明，学生在解题过程中思考方向单一，毋庸讳言，这样的题目设计可以起到“巩固课堂知识”的作用，但是对发散思维、逆向思维等训练价值不大。课堂引入数学游戏是对教学资源的有益补充。

数学游戏是趣味性很强的益智活动，有逻辑推理、策略方法、空间图形等多种形式，它通过设置特定规则，指引学生在阅读基础上对信息进行提取并整合，运用数学知识解决数学问题。学生参与游戏不仅可以巩固课内所学知识，还可以开拓思路，激发思考，锻炼和发展智力，观察、实验、比较、推理、猜想、分析、概括、归纳等多种能力与思维都得到开发和训练，有助于数学核心素养的形成与高质量发展。

二、引入数学游戏培养小学生推理能力的教学策略

小学生接受校园教育的时间短，知识储备和认知能力都处于低阶状态，他们对世界充满好奇，渴望接触并学习掌握新知识、新技能，利用他们求知欲强的特点，小学课堂引入数学游戏训练他们的数学思维是极好的窗口。

（一）培养学生据事说理的凭据意识

推理是个人思维方式与思考过程，具有很强的跳跃性，即接收信息后不需要对自身知识库搜索与复述，而是知识与技能的闪现利用，然后对事件呈现多种可能性的判断，经比较之后进行取舍并得出结论。在这个意义上说，推理过程是不可以被他人控制的；但推理毕竟是一种思考方法，有优劣之分，有规律可遁，因而推理也是可以被他人引导的。课内引入数学游戏，对于全新形式的数学题目，教师要注重做好解题示范，特别是如何充分利用已知条件，如何挖掘隐形条件，展示出推导结果的全程，给学生新的启发和联想。如：

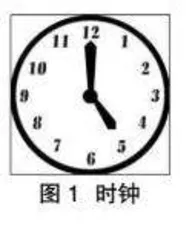
游戏1：下午5点整放学时，李华看看黑板上方的挂钟说：“当时针和分针重合时，我大概就走到家了。”问：李华步行回家，大概需要多少分钟？

问题分析：本游戏中，只有一个阿拉伯数字“5”，却要求参与者解答一个“具体的数值”，可见其中的数量信息及关系需要参与者从题目中挖掘，难度较大，教师可以把它分解成多个问题，逐步引导学生思考。

师：本题问“李华步行回家大概需要多少分钟”，实际上是问“五点钟时，分针过多少时间追上时针，两针重合”，相当于路程的应用题。与路程问题相关联的有哪些概念？

生：路程、速度、时间。

师：时针、分针的速度是多少？分别走了多少路程？题目并没有告诉我们任何信息，需要我们从时钟的特点入手。分针、时针都是围绕时钟的圆心运动，它们的运动速度是以角度来衡量的。分针每分钟走多少度？

生：分针一小时走一圈，360（度）÷60（分钟），分针每分钟走6度。

师：以此方法，求出时针每分钟走多少度。

生1：时针每小时走一大格，一大格等于30度，30度除以60分钟等于0.5度。

生2：分针1小时走完一圈12个大格时，时针才走一个大格，时针的速度是分针的十二分之一，6度÷12=0.5度。

师：正确。接下来找出它们各自走的路程。5点整时，观察时针与分针的位置，发现它们相隔多少度？

生： 150度。

师：这样，题目的问题变成了，时针与分针同向运动，分针的速度为6个单位，时针的速度为0.5个单位，时针先走了150单位后，分针需要多少时间赶上时针？利用设元法“设经过x分钟后，两针重合”，请你们列式并计算。

生：150+0.5x=6x，求得约27分钟后两针重合。

本题求得的结果是27.27……，是个无限循环小数，这样的题目设计会不会给学生造成困扰？事实上当然不会，因为学习数学不是为了解答具体的题目并记住答案，而是学习解决问题的数学方法，往更大的范围说是学习数学思想。任何推理都必须有其依据，有其因果逻辑，而不是臆想。本例引导学生逐步完成了推理与解答的过程，让学生明白“生活经验与常识也是知识的一部分，是可以作为推理的依据之一”，以此案例培养学生的“据理意识”，也就是解决问题的推理过程要“有根据”，要善于发现和挖掘根据，这样的推理才有说服力，才能得出正确的结论。

（二）培养学生数形结合的方法意识

恩格斯说过：“数学是研究数量关系与空间形式的科学。”揭示了数量与图形密不可分的关系。[2]教学中，教师要高度重视运用图形，将抽象的数量关系切换成图形进行直观表达。训练学生的推理能力，要引导学生养成运用图形分析数量关系的习惯，强化学生牢固树立数形结合的方法意识，它体现了数学的本质特点，运用在解答具体数学题目时，可以节省时间成本，提高正确率。如：

游戏2：李大伯将草绳剪成前、中、后三段，中段长度等于前段加后段，后段等于前段加中段的一半。只知道前段长5米，这条草绳一共长多少米？

问题分析：本题对于五、六年级的学生来说毫无难度，利用设元法，根据题目中的已知条件列式就很容易求得中、后段的长度，然后求和得出答案。但是中低年级的小学生尚未学习设元方法，如果引入图形即可轻松解决这一复杂问题。

解答过程：引导学生先画出中段，并把它均分为两部分；根据题目所言“中段长度等于前段加后段，后段等于前段加中段的一半”的提示，在中段下方画一条等长的线段，并做标记（如图2），图2中，线段b等于c（前段），而b+c=a，可知草绳中段的一半a是10米，得出草绳一共40米。

此例，在数学游戏中利用画图策略，将复杂的文字信息简化为图形，这个过程是已知条件的分析，综合运用了简化、概括、观察、推理等思维，是提升学生思维品质的有效手段。数形结合是学习数学的重要思想，其本质是突显数学规律和数量关系，从而理清思路，训练思维，领略数学世界的美妙。

（三）培养学生勾连知识的理论意识

数学游戏引入到课堂，不能为了游戏而游戏，而要与当天课堂所学的内容有关联，将课内知识迁移、扩展、运用到数学游戏中，让学生在参与游戏过程中及时复习，起到促进理解并巩固课内知识的作用。如学习统编版五年级上册“倍数的加减法”时，引入如下游戏。

游戏3：数学老师在黑板上写了1、2、3、4、5、6、7、8、9这九个数字，说：“同学们，你们把其中任意两个数字圈掉，再补上它们的差数，如圈掉8和3，就补上5，一直这样进行下去，如果最后两个数相减得到0，我就奖励他一个巧克力。”同学们立刻动笔计算，只有李华看了一眼题目说：我们不可能获得奖励的。他说得对吗？为什么？

问题分析：已学知识告诉我们，奇数±奇数=偶数，奇数±偶数=奇数，偶数±偶数=偶数。黑板上的9个数中共有5个奇数：1、3、5、7、9，根据游戏规则，让它们与偶数相减，仍然得到5个奇数；它们两两相减，得到两个偶数和一个奇数，余下这个奇数在接下来的游戏过程中，与任何一个偶数相减都将得到奇数，而游戏规则要求的最后结果得数为0，0是偶数，所以李华说得是正确的。

本例的推理过程是运用了课内学习的“奇偶数加减的规律”，理论知识与生活经验运用于推理才有迹可循，结论才有说明力。所以，学生在解答数学问题时，遇到已知条件不透明的，都应当联想到并运用课内相关知识。课内知识是理论，理论是生活经验与自然现象的抽象表达，是现阶段被人类证实的正确规律，具有高度的概括性，运用在推理思维中具有权威性，教师要引导学生牢固树立数学推理的“理论意识”。

（四）培养学生整合信息的筛选意识

数学游戏以文本形式呈现，从数量关系或因果逻辑来说，其中有些文字信息并不能揭示本质的问题，甚至可能并无实际意义，只是起到支撑和连接作用使句子结构完整，从而设置数学情境。此种情况下，学生探究数学问题时要学会筛选，要善于发现并提取关键信息，进而挖掘出“关键信息”所反映出的本质矛盾（问题），提高推理归纳能力。

三、结语

小学课堂引入数学游戏，学生在解析过程中，学会阅读并分析数据，学会信息整理与综合，探究其间的因果关联就是推理思维的运用，从具象思维向逻辑思维过渡，提高了自主学习、深入学习与终身学习的能力，有利于综合素养的高质发展。

参考文献：

[1]教育部.义务教育数学课程标准（2022年）[S].北京：北京师范大学出版社，2022.

[2]徐传开.中学生数学思维培养的策略[J].数学学习与研究，2012（21）：1.