“两位数乘两位数”单元整体设计

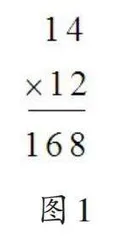
人教版数学三年级下册第四单元“两位数乘两位数”包括口算乘法、笔算乘法、解决问题等内容，对应的核心素养是运算能力，要求学生明晰运算的对象和意义，理解算理和算法之间的关系，感悟转化的思想方法，形成初步的推理意识。

基于对课程标准中学段目标、内容要求、学业要求等的分析，我们确定如下单元目标：①掌握两位数、几百几十数乘一位数（进位），两位数乘整十、整百数（不进位），整十数乘几百几十数（不进位）的口算方法，体会算法多样化；②经历两位数乘两位数的竖式形成过程，理解算理，掌握算法，提高运算能力；③经历从实际生活中发现、提出问题，进而分析、解决问题的过程，学会用连乘、连除两步计算解决问题。

一、精准前测，确定起点

此前，学生已经学习了“表内乘法”和“多位数乘一位数”。为了精准把握教学起点，我们从两位数乘两位数的算理理解水平、竖式记录过程两个方面对50名学生进行前测。

考查学生算理理解水平的题目如下：

结合点子图（图略），先说一说14×12的意义，再尝试计算。你可以在点子图上圈一圈、画一画，并用横式记录计算方法。

参照福建师范大学章勤琼教授提出的算理理解的五个水平层次，我们具化本单元算理理解水平：水平0，对前测问题无从下手；水平1，能理解两位数乘两位数算式的意义，并能根据运算需要对数进行重组；水平2，能在理解数的结构及算式意义的基础上，利用点子图表示计算过程并求出得数；水平3，能理解数的结构及算式意义，能借助点子图表征计算过程并得出计算结果，还能用数学语言说清楚先算什么、再算什么；水平4，能理解数的结构及算式意义，能形成自己的计算方法，能通过直观模型和数学语言表征计算过程，还能提炼出“基本算法”。

参照上述标准分析学生的作品，我们得出如下前测结果：处于水平0的学生有5人，占比10%；处于水平1的学生有18人，占比36%；处于水平2的学生有16人，占比32%；处于水平3的学生有11人，占比22%；处于水平4的学生有0人。这表明，90%的学生能理解两位数乘两位数算式的意义，能依据位值制拆分其中一个两位数，并通过多元表征得出结果，但大部分学生只是机械模仿计算流程，不会用数学语言表达计算过程，并且没有学生能改进算法，总结出通用算法。

结合点子图，大部分学生能用横式计算14×12，他们是否会用竖式记录计算过程呢？对此，我们也设计了前测题，引导学生借助点子图和横式（14×2=28，14×10=140，28+140=168）尝试写出竖式计算过程。前测后，我们整理出如下四种学生作品。

我们发现，15名学生受之前学习的两位数乘一位数乘法竖式的负迁移影响，写出如图1所示的“一层”竖式；8名学生虽然知道要分两层记录，但因为没有真正理解笔算乘法的本质而得出如图2所示的错误结果；15名学生能正确写出竖式，如图3、图4，但问及他们能否找到竖式与横式、点子图之间的联系，是否明白竖式中每一步的含义时，其中10人无法将三者关联起来，他们只是“依葫芦画瓢”地记录；其余12名学生没有写出竖式。因此，教学中，教师应注重从横式计算到竖式计算的过渡，引导学生沟通竖式、横式、点子图之间的联系，帮助他们深入理解算理，自然生成算法，实现算理与算法的融合。

二、整体分析，科学整合

在准确把握学生学习起点的基础上，我们认真研究教材编排的内在逻辑，进一步明晰各课时教学内容要达到的目标及学业质量要求，遵循层层递进、螺旋上升的原则，整合“两位数乘两位数”单元内容。

第一，把口算乘法的例1和例2两个课时的内容整合为一个课时。例1中16×3是三年级上册已经学过的内容，学生会笔算，本节课要学习的160×3的口算方法和笔算一致，都是基于位值制把两位数拆成几个十和几个一，先分再合地计算，学生可以通过迁移两位数乘一位数口算方法探究；例2中6×10可以调整为14×10作为新知教学，因为学生已经熟练掌握“6个十就是60”，所以他们很容易想到“14个十就是140”，这样他们就可以迁移14×10的计算经验探究12×20的计算方法。

第二，整合原本分为不进位与进位两个板块的两位数乘两位数笔算内容，形成连续课。由于算理理解直接影响算法掌握，所以第1课时指向学生深入理解乘法运算的基本原理，而不涉及竖式计算方法；第2课时侧重于竖式的构建，并通过竖式、横式、点子图的结合，帮助学生理解不同计算方法之间的联系。这样整合强调从算理理解到竖式记录的过渡，有助于学生深入理解算理，构建完整的算法体系。

第三，增加“乘法的前世今生”探索课。小学阶段整数乘法的学习分多个阶段：二年级上册学习表内乘法，指向乘法的意义和基本的口算；三年级上册学习多位数乘一位数，下册学习两位数乘两位数，这些乘法都是运用分与合、十进位值制等知识转化为表内乘法计算的，并要用竖式记录计算过程；四年级上册学习三位数乘两位数，重在算理和算法的迁移运用。通过梳理乘法的“前世”，学生能顺利地从前两个学习阶段拓展至探究乘法的“今生”（进入第三个学习阶段）。这样设计有助于他们用联系的眼光、系统的思维看待与思考学习内容，进而建立结构化认知。

三、任务驱动，建构体系

为更好地实施教学，我们以国庆花环表演活动为情景主线，设计贯穿单元教学的一系列任务。

第1课时口算乘法包括四个任务。任务一：结合参加国庆表演人数问题口算16×3，说说怎样算，不同算法间有什么联系。任务二：结合参加国庆表演人数问题口算160×3并说明这样算的理由。任务三：结合方阵人数问题口算14×10并说明这样算的理由。任务四：口算12×20，说说它和14×10的联系。

第2、3课时为连续课，每个课时分别设置两个任务。第2课时任务一为“结合方阵人数问题计算14×12，用横式写一写计算方法，并尝试用点子图表示计算方法”；任务二为“这些算法之间有什么共同点？尝试计算21×13，说说你的发现”。第3课时任务一为“你想怎样写14×12的竖式？说说这样写的合理性”；任务二为“找出竖式、横式、点子图之间的联系，尝试建构算法模型”。

第4课时旨在引导学生沟通不同阶段所学整数乘法之间的联系，形成结构化认知。本课时设置两个任务：一是提炼表内乘法、多位数乘一位数、两位数乘两位数的本质；二是迁移已有运算经验，自主探究145×12的计算方法。

第5课时“连乘解决问题”任务一是探究解决“28个班级参加花环表演，每班42人，每个花环5元，每人1个花环，购买花环一共需要多少元？”问题的方案，说出思考过程；任务二是先分步计算，再列出综合算式。

第6课时“连除解决问题”任务一是从“学校为参加方阵表演的学生购买了60顶帽子，平均分给2个年级，每个年级有6个班，每班分得多少顶帽子？”中找出关键信息，探析解决问题的方法；任务二是先分步计算，再列出综合算式。

课程内容的结构化整合凸显了学习的整体性、连贯性和延续性，有利于培养学生的结构化思维。

（作者单位：白凌晓，襄阳市教育科学研究院；刘雪林，枣阳市第一实验小学教联体人民路校区）

文字编辑 刘佳