在理法融通中感悟乘法运算的一致性

“两位数乘两位数”是第二学段“数与运算”主题的内容，是在学生掌握了表内乘法，会计算两位数乘一位数、三位数乘一位数的基础上教学的。无论是整数乘法，还是小数、分数乘法，其本质都是计数单位与计数单位相乘、计数单位上的数字与计数单位上的数字相乘。教师如何在教学中凸显乘法运算的一致性，培养学生的数感、运算能力和推理意识呢？笔者以“两位数乘两位数”单元教学为例说明。

一、借助数的意义，建立知识关联

在认识数的学习过程中，学生积累了按群计数的经验，能根据位值制将一个多位数分解。教学中，教师借助点子图引导学生把数转化为计数单位的表征方式，基于计数单位理解乘法算式的意义，表达算理，体会“整十数乘一位数可以以‘十’为单位计算；两位数乘一位数可以分别以‘十’和‘一’为单位计算，再合并”，为研究整十数乘整十数、两位数乘整十数的算理与算法奠定基础。

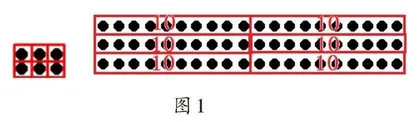
新课伊始，笔者出示2和20，请学生数出相应数量的小棒，说一说数的过程，以及它们分别表示什么意思。学生回答：一根一根地数，数两次就能数到2，2表示2个一，它是一位数；要数出20，可以一根一根地数20次，也可以一捆一捆地数（每一捆10根小棒）数两次，20是两位数，表示20个一或2个十。接着，笔者请学生回忆怎样计算2×3和20×3。学生回答：利用乘法口诀可以直接算出2×3=6；而计算20×3，要先算2×3=6，再在6的末尾添一个0，得出60。然后，笔者出示点子图（如图1），请学生找一找2×3=6中的6在点子图的哪里；20×3=60的积中的6和十分别在点子图的哪里。

通过圈画，学生发现60中的6实际上是6个十，2×3算的是2个十乘3，得6个十。笔者追问：为什么计算2×3时用乘法口诀计算后可以直接写6，而计算20×3时用乘法口诀计算后还要在6后面添一个0？学生指出：第一个6表示6个一，6个一就是6；第二个6表示6个十，在6后面添一个0才是60。最后，笔者请学生回忆23×3的口算方法，并将2×3和3×3的口算过程、结果与点子图建立联系。

通过以上对比分析，学生初步建立了数的概念与乘法运算的关联，体会到不管是一位数乘一位数还是两位数乘一位数，都是在用表内乘法计算计数单位的个数；由于两位数的计数单位既有“十”又有“一”，所以需要先算出几个“十”和几个“一”，再合并。

二、立足计数单位，打通算法关联

多位数乘一位数，由于其中一个因数的计数单位是“一”，计数单位与计数单位相乘产生的新计数单位与另一个因数的计数单位相同，学生难以发现两个因数的计数单位也参与了运算，如2个十乘3个一得6个十（“十”由“十”乘“一”得到）。整十数乘整十数，计数单位与计数单位相乘会产生与原本两个因数的计数单位不同的新计数单位。教学中，教师要引导学生根据计数单位相乘的意义对新的计数单位是多少进行正向和逆向推导，逐步把整数乘法的算法统一为“计数单位乘计数单位，个数乘个数”。

课堂上，笔者引导学生思考20×30可以怎么算，用自己的方法计算，并借助点子图说明这样算的道理。学生得出如下四种计算方法：①先算3×2=6，再在6后面添两个0；②20×3=60，60×10=600；③2×30=60，60×10=600；④3×2=6，6×100=600。针对方法②和方法③，笔者追问：60在点子图（如图2、图3）的哪里？为什么要再乘10？

借助点子图，学生发现方法②中的60可以看成20个一乘3，方法③中的60可以看成30个一乘2，它们都表示60个一，再乘10是因为图中还有10个这样的60。针对方法④，笔者追问：6在点子图的哪里？100从哪儿来？通过观察和交流，学生得出：在点子图（如图4）中，100由“十”乘“十”得到，即“百”，6是“百”的个数。

笔者适时总结：“从数的意义看，计数单位‘十’与‘十’相乘得到一个新的计数单位‘百’”，并追问：方法④中，2和3这两个数相乘是在算什么？为什么相乘后在积末尾添两个0就能得到正确结果？通过讨论交流，学生发现：20里有2个“十”，30里有3个“十”，2乘3算的是积的计数单位的个数，在6后面添两个0是因为新的计数单位是“百”。

学生理解20×30的计算过程后，笔者设疑：20×30中，两个因数的计数单位“十”和“十”相乘产生新的计数单位‘百’。回头看一看，口算20×3时，两个因数的计数单位有没有相乘呢？经过激烈的讨论，学生达成共识：将20看作2个“十”，3看作3个“一”，任何数乘1都得它本身，“十”乘“一”还是“十”，与20的计数单位“十”相同，因此我们误以为两个乘数的计数单位没有相乘，实际上则不然。

这样教学，学生体会到整十数乘一位数和整十数乘整十数口算方法的一致性，都是先用两个乘数的计数单位相乘得到新的计数单位，再算出新计数单位的个数。

三、基于整体视角，完善认知结构

乘法运算的原理是等合计数单位的个数。教学中，教师可以借助点子图引导学生在用不同计数单位计数的过程中，对接算式中每一个数、每一步计算所表示的意义，以此贯通整数乘法算理的理解。

课堂上，笔者聚焦22×30和22×33的计算方法展开教学。学习22×30时，笔者请学生借助点子图探究其计算方法，然后在小组里说一说怎么算。交流环节，一名学生借助点子图汇报：先计算22×3=66，再在积的末尾添一个0。另一名学生补充：也可以先将22拆成20和2，计算20×30=600，2×30=60，再将600与60合起来得到660。针对第一种方法，笔者提问：22×3算的是什么？为什么要在它的积的末尾添一个0？学生思考后回答：22×3算的是计数单位“一”的个数，添0是因为有10个22×3。针对第二种方法，笔者设疑：同样是两位数乘30，为什么前面口算20×30时只需算一次“2×3”，这里口算22乘30，需要算两次“2×3”？学生思考后解释：20是整十数，由计数单位“十”构成，22是两位数，由计数单位“十”和“一”组合而成，第一次“2×3”算的是6个百，第二次“2×3”算的是6个十。笔者总结：当因数是整十、整百数时，可以用一个计数单位去数（算），当有一个乘数是非整十、整百数时，需要用多个计数单位去数（算）。

学习22×33时，笔者请学生先猜想“如果用‘2×3’计算22×33，要将‘2×3’算几次”，再借助点子图验证。学生操作后，发现如下3种拆分方法：①20×30=600，20×3=60，2×30=60，2×3=6，600+60+60+6=726；②22×30=660，22×3=66，660+66=726；③20×33=660，2×33=66，660+66=726。不管哪一种方法，都要将“2×3”算4次。笔者适时将点子图简化成如图5所示的样子，并出示22×33的竖式，引导学生找出竖式中的各部分与口算方法的联系。学生通过观察，明确了笔算乘法与口算乘法的计算道理一样，都要确定运算后新的计数单位是什么、有多少个，不同的是笔算乘法省略了不同计数单位上乘出的数合并的过程，并且在记录上做了简化。

在计数单位的统领下，学生对乘法算式中积的位值意义有了更深层次的理解，感受到整数乘法运算的一致性。

（作者单位：宜城市窑湾小学）

文字编辑 张敏