多维建构，培养空间观念

《义务教育数学课程标准（2022年版）》指出：“引导学生通过观察、操作等活动，沟通立体图形之间的联系，以及平面图形与立体图形的关系，增强空间想象力。”本文以人教版数学六年级下册第三单元“圆柱的表面积”教学为例，探究如何在几何图形的教学中引导学生借助折纸等活动，理解立体图形与其平面展开图的关系，增强空间观念和想象力。

一、化直为曲，突破难点

在本节课之前，学生已经学习了长方体和正方体的特征，掌握了其表面积、体积的计算方法，认识了圆，会进行圆的周长和面积计算，对于如何探究立体图形的表面积和体积具备一定的知识基础和活动经验。圆柱作为旋转体，既有平面图形又有曲面图形，因此，如何在圆柱表面积计算的教学中突破曲面面积计算的难点，成为本节课要重点探究的问题。

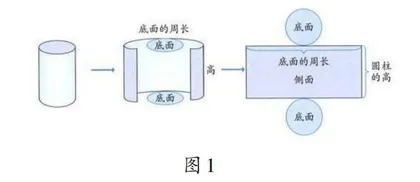
教师出示图1，即教材上的圆柱展开图，并提问：观察下图，你能发现什么？

教师试图引导学生根据教材示意图理解圆柱的底面周长和高与长方形的长和宽之间的联系，但这种没有让学生经过实际操作的教学方式，难以帮助学生突破曲面面积计算这个难点。因此，教师及时调整教学策略，通过“化直为曲”的操作辅助学生理解。

教师出示以下任务：用一张长方形纸片可以创造出什么样的立体图形？想好后折一折、围一围，验证自己的想法，然后展示交流。学生创造出不同的立体图形，如圆柱、三棱柱等。教师让学生仔细观察所折出的立体图形，并提问：这些图形与长方形的长和宽有什么关系？此时，学生将手中的立体图形不断地展开又合拢，通过操作、观察和比较，获得新的认识。折出三棱柱的学生说：“我发现三棱柱的高其实就是长方形的宽，而底下三角形这个面的三条边长合起来就相当于长方形的长。”折出圆柱的学生一边演示一边说：“当我把它这样卷起来的时候，长方形的宽变成圆柱的高，长方形的长变成圆柱的底面周长；当我把它这样卷起来的时候，长方形的长变成圆柱的高，长方形的宽变成圆柱的底面周长。”还有的学生说：“其实把这些立体图形放在一起观察，就会发现这些立体图形的高都是长方形的宽，它们的底面都是长方形的长围起来的，所以底面周长都相当于长方形的长。”

在“化直为曲”的活动过程中，学生通过操作、观察、比较都能直观地发现：这些立体图形的侧面其实就是一个长方形，并且初步感知到立体图形的底面周长和高与长方形的长和宽之间的联系，轻松地突破了本节课的难点。

二、多维建构，强化认知

建构主义学习理论认为，学习活动不是由教师向学生传递知识，而是学生根据外在信息自主建构知识的过程。教师结合学生已有认知，通过如下3次建构活动达成本节课的核心目标。

1.第一次建构——创造圆柱，建构圆柱侧面积计算模型

在创造立体图形的活动中，学生利用长方形纸片创造出不同形状的圆柱，已经基本完成了圆柱侧面积的模型建构，并且能用数学语言准确描述圆柱的侧面与其展开图之间的关系，理解侧面积的计算方法。这是对圆柱侧面积的第一次建构。

2.第二次建构——借助动态想象与推理，建构圆柱表面积计算模型

当学生完成对圆柱侧面积的建构之后，教师引导学生借助想象逐步推导圆柱表面积的计算方法。教师提问：“圆柱的侧面积就是它的表面积吗？”学生认为，还要再加上两个底面的面积才是其表面积，并且这两个底面是大小相同的圆，所以“圆柱的表面积=侧面积+2个底面积”。教师继续问：“应该如何计算底面积？”一名学生回答：“可以用尺子测量圆的直径，算出半径，根据圆的面积公式计算。”另一名学生回答：“测量会有误差，并且生活中很多圆柱形物体是无法用尺子量直径的。”学生一致认为测量直径的方法并不通用，但一时没有想到更好的方法。教师提示：“想一想刚才我们是如何创造出圆柱的，圆柱的侧面展开图与长方形的长和宽有何关系？”学生恍然大悟：长方形的长相当于底面周长，因此可以利用圆的周长公式反推出圆的直径，再算出半径，这样就可以利用圆的面积公式算出底面积了。教师赞同学生的说法，并总结：并不是所有圆柱的侧面积都可以展开变成长方形，我们要靠想象把圆柱和长方形的相关数据联系起来，这样就能更好地解决问题。学生通过讨论、比较完整建构了圆柱表面积的计算模型，找到了求圆柱表面积的关键。

3.第三次建构——沟通知识联系，完善认知体系

课堂小结环节，教师让学生比较圆柱表面积的计算方法与长方体表面积的计算方法有何异同点，学生发现：它们都是用侧面积加两个底面积计算，只不过圆柱是曲面图形，其侧面是一个长方形（正方形）的面，而长方体的侧面由四个长方形组成。

从直观体验到想象推理再到归纳概括，学生从具象到抽象地完成了圆柱表面积计算模型的3次建构，完善了认知体系，发展了空间观念。

（作者单位：黄石经济技术开发区·铁山区黄石市外国语学校）

文字编辑 张敏