基于“理解数学”的课堂教学研究

［摘  要］ “理解数学、理解学生、理解教学”简称“三个理解”，是章建跃博士所提出的教学理念. 随着新课改的深入推进，该理念应用频率越来越高. 研究者以“平面向量的加法运算”为例，从“概念导入，揭露教学意义”“建构概念，暴露运算本质”“剖析概念，研究运算定律”“概念应用，解决实际问题”“深化概念，提炼思想方法”五个环节设计教学活动，旨在帮助学生在深刻理解数学知识的同时，提升思维能力和学习能力，并发展数学学科核心素养.

［关键词］ 理解数学；平面向量；课堂教学

在“三个理解”的基础上实施课堂教学，可有效提升课堂教学效率，促进学习能力与数学素养的发展. 那么，何为“理解数学”呢？研究发现，教材作为知识传递的基本载体，在以教材为本的基础上研究数学概念，可铸就“数学细胞”；思维是数学的体操，在以数学思维发展为基本目标的基础上探索知识结构，可强健“数学骨骼”；思想方法是数学的灵魂，在渗透思想方法的基础上实施解题教学，可丰满“数学血肉”. 因此，“理解数学”就是以教材为本，重视数学思维的培养和数学思想方法的渗透，通过概念教学、知识结构梳理与解题教学等手段完善学生认知体系的过程.

教学分析

平面向量的加法深刻反映了向量的本质特性，是向量章节中的基础运算之一. 然而，学生对这部分内容的理解程度并不理想，主要原因是许多教师认为这部分内容相对简单，因此在教学过程中往往一笔带过，导致学生出现了“懂而不会”的现象. 也有部分教师认为，学生已经学过物理学科中的运动合成相关内容，他们对向量加法的理解相对容易. 因此，这部分教师直接向学生展示向量加法的三角形和平行四边形法则，跳过本质分析环节，直接进入应用阶段，致使学生对向量加法运算出现了“一知半解”的现象［1］. 为了改善这一状况，笔者基于“理解数学”的理念，对这部分内容的教学进行了深入的探讨和分析.

教学构想

教材是教学的基本载体，教材中的知识只是静止的“半成品”，教师在课堂上挖掘教材的教学功能，通过重组等方式揭露数学思想是理解数学的根本. 因此，课堂教学的首要任务就是通过观察与分析教材中的知识内容，挖掘其潜在的思想，此为提高教学效率的关键一步.

1. 概念导入，揭露教学意义

在建构主义理论的指导下，以向量运算的本源作为教学的起点，结合学生现有的认知经验来创设问题，可唤醒学生原有的认知经验，激活他们的思维，从而让学生初步理解向量加法运算的价值与意义.

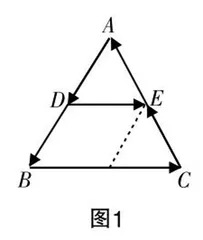
问题1 在平面几何领域，三角形中位线定理大家都不陌生. 现在，请大家思考：是否可以从向量的角度来描述三角形中位线定理？

设计意图 三角形中位线定理是学生所熟知的内容，向量也是他们已经掌握的知识. 要求学生从向量的角度来描述三角形中位线定理，不仅能帮助学生复习向量、共线向量以及相等向量等概念，还能让他们感受到数学知识间的内在联系，为本节课的向量加法运算教学打下坚实的基础.

师：关于三角形中位线定理的证明，以往采取的是什么方法？

生1：坐标法与几何综合法.

问题2 如图1所示，既然可以使用向量来描述三角形中位线定理，那么是否可以利用其他向量来揭示与之间的关系呢？换言之，能否通过向量运算来证明这个定理？

设计意图 此为一个典型的问题，旨在引导学生得出肯定的结论. 它鼓励学生主动思考，认识到自己在认知上的不足，并感受到学习向量加法运算的必要性. 有专家指出，如果没有运算，那么向量只是一个“路标”. 因为有了运算，向量的力量无限. 想要理解这句话中的“力量”一词，就要深入探索向量的运算. 问题2引导学生的思维自然而然地进入了向量运算的领域，激发了学生利用向量解决几何问题的初步想法，并成功揭示了向量加法运算的教学意义与实际应用价值.

2. 建构概念，暴露运算本质

问题3 已知冰箱内有3个苹果，若往里面再放2个苹果，冰箱内共有几个苹果？可否从这个实例出发，说一说“2+3=5”所蕴含的运算规则是什么？

设计意图 对高中生提出这么简单的一个生活问题，令学生感到诧异，甚至有学生直接笑场，认为老师怎么会提出这么幼稚的问题. 然而，此问的核心在于揭示“2+3=5”所蕴含的运算规则，显然这是一个包含深刻道理的小问题. 数字加法的本质是求两个数的和，唯有属性相同的数量关系才具备累加的条件. 在这个问题中，3个苹果与2个苹果具备相同的属性，因此它们可以直接相加. 将这一特性类比迁移到向量的加法运算中，我们不禁要问：是否只有满足特定条件的向量才可以相加呢？

师：向量的本质特征是什么？

生（众）：既有方向，又有大小.

问题4 结合向量的本质特征思考：满足什么条件的两个向量具有相加的可能？向量相加时，应遵循什么规则？

设计意图 通过提问激发学生对向量本质特征的回忆，并提示学生：向量加法与向量的方向和大小密切相关. 问题4的提出旨在激发学生自主思考，引导他们从向量的几何表示角度展开分析. 显然，将两个有方向的线段进行叠加，受方向的限制，与单纯数字的累加有所区别. 俗话说“不愤不悱，不启不发”，问题4成功激发了学生的思考和疑惑，使他们明确向量加法与数字加法不完全相同，向量加法运算必然有一套独特的规则，这为揭示向量加法运算的本质奠定了基础.

问题5 假设向量a，b是同向向量，它们相加会怎样？如果向量a，b为相反向量，那么它们相加又会怎样？设尝试分析以上两个问题，思考向量相加的基本规则，并提炼相应的数学表达式.

问题6 两个不共线的向量相加，遵循什么样的规则？从物理学的视角来看，位移合成是指一个物体从点A经过点B到达点C，即经过两次位移抵达目的地. 这个过程的结果与物体从点A直接位移■抵到目的地是相同的. 即便点A，B，C并不一定位于同一直线上，仍然存在这个式子. 那么，该式是否在所有情况下都成立呢？

设计意图 跨学科教学是新课程标准对数学教育提出的要求，它强调将不同学科的知识融合在一起. 虽然向量与位移之间存在着显著的相似性，但如果教师仅仅告诉学生物理运动合成与向量加法法则之间的联系，学生可能无法真正理解数学的深层含义. 相反，从数学家发现向量加法运算的过程入手，通过“再创造”教学内容，可以激发学生的思考，让学生像数学家一样主动探索，从而更深入地理解向量加法运算的本质.

3. 剖析概念，研究运算定律

问题7 两个向量相加的规则大家已经有所了解，现在我们一起来思考：在同一平面内，多个向量相加，该怎么处理呢？

设计意图 数字相加是将多个数累加在一起形成一个总和，其累加过程遵循交换律与结合律. 本节课探索的是一个平面内的向量相加，同为加法运算，因此可以从加法运算规律的角度进行分析，即在同一平面内，多个向量相加的本质是将这些向量相加转化为两个向量相加（见图2）. 在向量相加的过程中，无论采用哪种结合方式，结论都是一样的. 据此，可以推断出向量加法运算同样遵循交换律与结合律，即（a+b）+c=a+（b+c）.

4. 概念应用，解决实际问题

例1 现在深入探讨如何使用向量加法来证明三角形中位线定理.

例2 如图3所示，此为一个轮渡口，渡船从点A处出发，正常以5 km/h的速度垂直驶向对岸的点D处，明确水的流速为向东2 km/h.

（1）用向量分别表示水流速度、渡船的航行速度以及渡船实际航行的速度.

（2）渡船实际航行的速度与方向分别是什么？

设计意图 这两个例题旨在加深学生对向量加法的理解，并体验向量加法在解决几何问题和实际问题时的便捷性. 尤其是例2的应用，让学生对向量及其加法的实际应用价值有了更深入的认识，进一步感知数学与日常生活的紧密联系.

5. 深化概念，提炼思想方法

问题8 为什么在同一平面内不共线的多个向量相加，最终可以转化为两个向量相加呢？由什么原理可以作解释呢？

设计意图 学生的认知发展遵循由浅入深的规律，那么数学教学同样遵循由易到难、逐层递进的规则. 虽然学生在该阶段尚未接触线性相关的内容，但向量的加法运算中却蕴含了这种思想. 教师在课堂上适时地进行引导和渗透，能够激活学生的思维，为后续教学夯实基础. 调查显示，许多大学生将向量组的线性相关性视为学习上的一个难点. 因此，在本节课中适当引入与之相关的思想方法，可为学生未来学习n维向量组的线性关系做好准备. 需要注意的是，在此环节不必使用严格的数学术语，而可以应用易于理解的数学语言进行解释，引导学生感知向量加法的内涵.

由共线向量相加可知，共线向量具有相互表示的特性，而这一特性在不共线向量中是不存在的，这也是不共线向量无法位于同一直线上的原因. 综上探索，下节课可以引导学生自主将向量加法运算推广到向量数乘运算，让学生在“理解数学”的基础上实现知识与研究方法的迁移.

思考与感悟

1. 研究向量加法产生的原因是理解数学的基础

用代数法研究几何问题是向量加法运算产生的基础. 笛卡尔发明的坐标系，为人类探索几何问题提供了服务，但莱布尼茨认为，“尽管笛卡尔的坐标系统将几何量转化为代数方法的分析，但不是几何量之间的直接运算，有时是复杂的. 这种把代数用于几何是一个正确的方法，但不是最好的.”［2］在莱布尼茨思想的影响下，莫比乌斯与格拉斯曼研究了有向线段的加法运算. 他们认为，如果把AB视为BA的相反量，只要能确定点A，B，C均处于同一条直线上，那么AB+BC=AC恒成立. 经过大量实践验证，他们发现在点A，B，C不处于同一条线上的情况下，该式依然成立. 这一发现被称为向量加法的三角形法则，即

一旦学生对向量加法的成因有了清晰的理解，他们便会对这一运算产生积极的情感反应. 此外，对成因的深入分析还能提升学生的数学理解能力，为新知的探索打下坚实的基础. 在本节课中，教师在引导学生正式探索向量加法运算之前，已经与学生一起探讨了向量加法运算的形成过程. 这样做让学生在积极主动的状态下接受并深入研究新知，为构建完整的知识体系打下了基础.

2. 关注向量加法运算的本质是理解数学的核心

本节课的主题是向量加法运算，既然是运算，必然涉及运算法则. 那么，向量加法的运算法则是什么呢？带着这个问题去学习和探索，首先需要了解向量加法运算的本质，这是理解向量加法的运算法则的关键. 在加法运算中，“+”符号代表的是一种运算方式，而其背后所隐藏的规则才是我们应当深入探究的核心.

向量除了具有与数相同的大小属性外，还具有方向这一关键属性，因此向量的加法与数的加法有所不同. 相同或相反方向的向量可以在一条直线上进行研究（见图4），反方向的向量大小可以通过负值来表示. 在这种情况下，向量的加法运算与数的加法运算基本一致，即相加后不再保留各自原有的特性，相加的结果是一个新的向量.

如果两个向量不是共线的，那么它们相加的结果本质上是这两个向量的合成，意味着原本参与相加的两个向量的大小和方向保持不变（见图5）.

向量加法运算的深入探讨，可促使学生从真正意义上理解向量加法运算的本质，达到理解数学的目的.

总之，基于“理解数学”的课堂教学是一个值得深入探索与研究的话题，尤其是在新课标的背景下，想要让核心素养落地生根，就要在理解数学的基础上设计教学方案，实施教学，此为促进学生长期可持续发展的重要举措.

参考文献：

［1］ 吕松涛. 平面向量加法运算的本质及教学思考［J］. 数学通报，2020，59（9）：43-47.

［2］ 吕松涛. 基于问题驱动的高中数学向量教学研究［D］. 广州大学，2021.