让儿童在“一个经验”中构建高质量的数学学习

［摘 要］“一个经验”指学习者在与新知识相遇的过程中，形成对客观事物的现象和外部联系的能动认识，以及其具身接触、认识客观事物的完整过程。在小学数学教学中，可借鉴“一个经验”的形成过程及机理构建高质量的数学学习，突出价值性、完整性、具身性和审美性这四个特征。

［关键词］“一个经验”；价值性；完整性；具身性；审美性

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）11-0014-04

何谓“一个经验”？相关研究并不多见，这为我们的研究和探索提供了“创造”的空间和可能。杜威曾经打过一个类似的比方：“如果我们想象一块向山下滚动的石头拥有了一个经验，就可以得到一个‘一般化’的描述。石头从山上开始持续向山下滚，直到停止。想象是美好的：其一，整个过程是有价值的；其二，获得了到山下的最终结果；其三，它对途中所遇到的事物，以及推动和阻碍其运动、影响其结果的因素充满兴趣；其四，它会根据运行过程中阻滞和促进其滚动的功能与感受去做事；其五，最后是终止并与之前的连续运动的积累联系在一起……此时这块石头就拥有一个经验、一个带有审美性质的经验。”从石头下山的隐喻来看，“一个经验”的学习中，“一个”不仅指知识学习的一个完整时间单位，还指知识学习的一个完整经历。“一个经验”是指作为学习者的人在遭遇新知识的过程中，通过感觉器官获得有关客观事物的现象和外部联系的能动认识，以及其具身接触、认识客观事物的完整过程。“一个经验”的形成具有多个特征，其中四个特征尤为主要，即经验的价值性、经验的完整性、经验主体的具身性和过程的审美性。下面将论述如何利用“一个经验”建构高质量的儿童数学学习。

一、“一个经验”带来的数学教学应具备价值性

关于价值性，学界有诸多研究。马克斯·韦伯将理性作为研究对象，把主体行为划分为工具的合理性与价值的合理性两个范畴，即工具理性与价值理性。其中，“工具理性是指通过控制主体行为来使其效用最大化，其核心是行为达成的结果，而对行为本身是否有价值，则无须过多关注；价值理性强调行为本身的价值，而非所采取的手段与结果呈现”。由此观之，数学知识也有工具理性与价值理性之分。数学学习固然要重视工具理性，但价值理性更为重要。在“一个经验”中，价值理性应置于首位。北京教育学院季苹教授在《教什么知识：对教学的知识论基础的认识》一书中指出：“每一个知识都兼具事实性、概念性、方法性、价值性四个侧面。没有概念概括，客观的事实或现象只能是经验；没有方法运用，概念或原理只能是词语符号；没有价值取向的揭示，方法只是机械的步骤。从事实到价值，理解逐层递进，知识也就愈发有‘意义’。”若论数学的价值性，可以更多聚焦于“这个”数学知识为何诞生？没有“这个”知识是否可行？“这个”知识对生活应用及数学自身发展有着怎样不可替代的作用？若数学教学能在这些方面着力，学生便能体会到数学知识在“来龙去脉”和“来之不易”方面的价值意蕴。

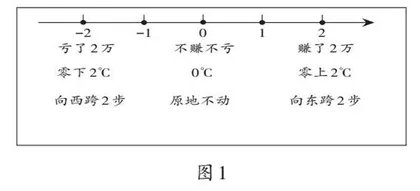
比如，教学“负数的认识”时，可以从生活和数学两个维度引导学生感悟负数产生的必要性。围绕“-2、0、+2”这组数，让学生列举生活中对应的例子，并将这些例子呈现在数轴上（如图1）。接着引发学生思考：“假如生活中没有负数，你觉得可以吗？”鼓励学生充分感悟、大胆表达，最终形成共识：生活中不能没有负数，若没有负数，就无法表示与正数意义相反的量。

进而，出示题目“数学课上正在进行抢答比赛，规定答对一题加1分，答错一题扣1分。小刚答对6题、答错4题，小林答对3题、答错5题，小刚和小林各得了多少分？”学生很快算出结果：小刚为6-4=2（分），小林为3-5=-2（分）。教师再利用问题“假设在数学上没有负数，你觉得可以吗？负数起到了什么作用？”引发学生思考。学生在计算结果面前真切感受到：不能没有负数，没有了负数，较小的数减较大的数就难以得出结果。此时，负数的本质逐渐清晰：在生活维度，负数可表示与正数意义相反的量；在数学维度，负数可使减法运算封闭。这样的本质，恰恰体现了知识的价值性。教学若能着力于此，让知识真正融入学生的知识“视界”，就能使学生产生强烈的共情心理，进而催生强大的学习力。

二、“一个经验”带来的数学教学应具备完整性

数学的整体性毋庸置疑。希尔伯特在1900年就指出：“数学学科是一个不可分割的有机整体，它的生命力依赖于各个部分的联系。”数学家阿蒂亚也表明：“数学的统一性与简单性都极其重要，因为数学的目的就是用简单而基本的词汇去尽可能多地解释世界。”一个重大的数学问题通常是在实践中提出，通过建立数学模型寻求解题方法，直至最终解决，这一过程需要不同数学分支相互联系、渗透。

当下，小学数学教学具有严重的碎片化倾向，以“例题+课时”的方式应对日常教学，呈现“只见树木，不见森林”的状况——只关注当前教学内容，不关注知识点在单元中的位置；“砍头去尾烧中段”——对知识的来龙去脉不闻不问。数学教学需突破“例题+课时”的模式，努力向“核心概念+单元”转变，让教学具有整体性。

例如，教学“分数的基本性质”时，不能拘囿于教材内容，要在合适时间内，帮助学生回溯、展望与“分数的基本性质”相关的知识，构建完整的知识结构。比如，呈现三年级下册学生学习“分数的初步认识”时出现的典型错误（如图2），明确只能填1/2而不能填2/4的根本原因是“数值相等，意义不同”；再现“商不变的规律”、展望六年级的“比的意义”，让学生明白它们与“分数的基本性质”形式不同、原理相通；重温“小数的意义与性质”，使学生知晓其与“分数的基本性质”特殊与一般，本质相同。以“分数的基本性质”为线索，串联起前后关联知识，让学生在“同与不同”中构建系统的知识结构。

再如，新修订的数学教材将过去的“认识假分数”内容改为“分数的意义和加减法”中的例2，把假分数教学纳入“分数的意义”这一大概念之下，从“度量”角度揭示假分数概念。教师可围绕“如图3，如果以第1根粉彩带为标准，第2根、第3根、第4根分别是多少根粉彩带的长？”这一研究主线，引导学生操作、想象和思考。学生基于“第2根紫彩带是第1根粉彩带的长的2倍”这一已有知识，对“第3根黄彩带、第4根绿彩带分别是多少根粉彩带的长”这一核心问题深度思考。学生意识到，过去“以1根粉彩带为标准”的经验无法解决新问题，从而对新标准进行想象与尝试，进而感悟到“1根粉彩带的几分之一也可以当作标准”，由此得出：第3根黄彩带是3/4根粉彩带的长，第4根绿彩带是4/3根粉彩带的长。这样，学生自然感受到：分数除了像以前一样“分”出来，还可以“量”出来。课末再展现“分数与除法的关系”“分数与比的关系”，学生就会进一步感知“分数还可以算出来”“分数还可以比出来”。如此教学，分数的意义便“饱满”且“完整”了。

三、“一个经验”带来的数学教学应具备具身性

有研究指出：“穿黑衣会让球员更容易犯规，握着咖啡能让人更加热情……心理学前沿研究结果显示，知识存在于行动之中，表现在身体上，蕴藏在体验里。”伟大的观念始终与身心体验紧密相连，其不仅要在生活中有所运用，还应具备防止知识蜕变为惰性的特质，这或许正是教育的核心问题所在。

《义务教育课程方案（2022版）》指出，要加强课程内容与学生经验、社会生活的联系，强化学科内的知识整合，突出学科思想方法和探究方式的学习，加强知行合一、学思结合，在“做中学”“用中学”“创中学”与“合作中学”的真实情境中培养学生综合运用知识解决问题的能力。然而，在实际教学中，教对学的遮蔽、知与识的割裂等现象依然存在。在这种教学模式下，学习者未能经历知识的建构过程，更像是旁观者，仅看到作为结果的知识。荷兰著名教育家弗赖登塔尔认为，数学学习最正确的方法是“再创造”。“再创造”意味着学生具身经历知识的探究、发现与迁移过程，并通过这一路径生成、丰富数学学科学习的主体性经验。

以教学五年级“圆的认识”一课为例，教师先让学生用圆规在纸上画圆，接着引导学生用剪刀将圆剪下，最后让学生摸一摸、折一折圆形纸片，并说一说有哪些感受。这一系列“行为学”操作极具教育价值：学生经历了圆的形成过程，感受到圆是平面上的曲线图形，明确了定点表示圆心、定长表示半径，体悟到半径有无数条且都相等，以及直径也有无数条且都相等。在练习阶段，教师给学生提供一个残缺且看不到圆心的圆片，让学生想办法找出圆心位置。此时，学生思维活跃，在充分动手操作与思考后，想出多种方案：把纸片对折再对折，折痕相交处即圆心；在圆上任意找两点，将其连接成线段，作出该线段的垂直平分线，延长平分线与圆相交会得到两个交点，交点间的线段就是直径；用直尺在圆中量长度，找到最长线段，即直径，取直径中间点就是圆心。

在真实、复杂的问题情境中，让学生亲身经历、具身探索，他们才有可能获得主体学习经验。因此，学生只有以主体角色参与知识的发生、生成与延展过程，他们的学习经验才能蓬勃生长。

四、“一个经验”带来的数学教学应该具备审美性

“一个经验”具有情感性与内隐性，审美的经验只是一种情感强化且集中的“一个经验”。知识与情感“双轮驱动”理论表明，情感宛如串起珍珠的丝线，将学习过程中诸多如“珍珠般”的经验连接起来。正是由于情感的存在，教学才具备审美性，并与知识统一为“一个经验”。情感对于经验而言，是一种具有聚合力量的“黏合剂”，对“一个经验”的形成起着不可替代的作用，能使散乱无序的经验逐渐趋于完满。在“一个经验”形成过程中，与情感相伴而生的感受便是审美。

在数学教学中，“一个经验”的教学既蕴含知识本身完整的结构之美，也包含伴随或催生知识所产生的学习兴趣、学习意志及学习情感所带来的意义之美。“量角器诞生记”一课的教学，堪称“经验与审美相伴而生”的典范。首先，教师展示两个角∠1和∠2（如图4-1），让学生猜猜，哪个角大？大多少？在解决大多少的问题时，教师出示若干个10°的木制小角学具，让学生用这些小角比较两个角的大小，从而得出“∠2用了4个小角，∠1用了3个小角”（如图4-2），初步显现角的度量属性。在“能不能想个办法，既保留它的准确性，又改变它操作麻烦的缺点呢？”这一问题的驱动下，学生提出“把小角拼起来”“用胶带把小角粘起来”等朴素想法，教师顺势呈现18个小角动态拼成一个半圆的过程（量角器的初始形态）。随后，让学生用18等分的量角器雏形量出图中（如图4-3）各角的大小。在学生得出“∠3有4个小角，∠4有12个小角，∠5有5个小角多一点”后，教师追问：“多出的这一点到底是多少？如果我们一定要知道到底是多少，有什么办法？”引导学生改造原先量角器的雏形，得到“把每个小角再分成10个小小角”的方法。如此，一个半圆等分为180个小角的量角器便形成了。最后，让学生用现有的“量角器”度量某个角的度数。学生感觉从右边数很麻烦，产生“要是能从图中直接读出来就好了”的心理需求。教师乘机呈现外圈刻度线，并依次顺向标上刻度，一个完整的量角器就此诞生。

数学，若将其装扮起来，就是一位光芒四射的“科学女王”。然而，如果在数学学习中只关注逻辑、公式、定律、公理，那么这位“科学女王”就会变成光学仪器下的骨架。在上述教学中，出现了“量角器为什么会有若干个角？”“为什么分那么细的角？”“为什么要做成半圆形的？”“为什么要有内圈和外圈两圈的刻度？”这些“本原性”问题的追问，让学生深刻感受到数学探索过程中的执着与坚持、论证过程中的务实与严谨、创造过程中的开拓与超越等情感要素。这些感受即为审美经验，或者说是“一个经验”审美性的重要组成部分。由此可见，“一个经验”是“行”与“爱”的完美统一。正是这种“行”与“爱”的完美统一，使教学不再将功利性、碎片化的知识结果作为学习的唯一追求。教学既要给予学生整体性结构化的知识，或者说基于知识内容的完整经验，又要关注学习本体在学习过程中所获得的积极心理倾向。

［ 参 考 文 献 ］

[1] 杨九俊，王彦明，刘玮.新课堂“怎么办”［M］.南京：江苏凤凰教育出版社，2024：213-219.

[2] 占梦君，谢莉花.超越工具理性：职普融通的价值维度、目标向度与推进策略［J］.教育与职业，2024（10）：15-22.

（责编    金    铃）