巧设铺垫题，促进学生思维拾级而上

［摘 要］人教版教材中的某些单元练习题后标着“？”的问题为该单元的拓展练习题，旨在拓展知识，提升学生的数学思维和解决问题能力，教师应挖掘这些题目的教学潜力。文章以“百僧百馍”问题为例，分析学生解题过程，了解学生思维水平，并在此基础上设计铺垫题让学生独立解决，以提高解题能力，掌握解题模型。

［关键词］“百僧百馍”问题；铺垫题；百僧百馍

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2025）11-0056-03

一、研究背景

人教版教材四年级下册“鸡兔同笼”的课后练习中编排了一道标记有“？”的“百僧百馍”问题：“100个和尚吃100个馒头。大和尚一人吃3个，小和尚3人吃一个。大、小和尚各多少人？”

笔者在学生解决“百僧百馍”问题之前设计铺垫题，希望能够提高学生的数学问题解决能力，培养学生核心素养。

二、研究路径

本研究选取了一所乡镇学校中四年级两个班级，共计82名学业水平相当的学生作为测试对象。

研究过程分为七个步骤。

①对学生进行初次“百僧百馍”问题测试。

②分析测试结果，探究学生的解题思路和遇到的难点。

③依据分析，并结合题目的特性，设计一组相应的铺垫题。

④学生独立完成铺垫题。

⑤对学生进行第二次测试，包括“百僧百馍”问题以及相应的变式题。

⑥三个月后（即五年级开学初），对学生进行第三次测试。

⑦进行分析研究，并得出研究结论。

三、教学实践

（一）第一次测试结果及分析

“百僧百馍”问题出自明代程大位所著的《算法统宗》，它要求学生在未学习列方程等方法前，辨识此类型问题与“鸡兔同笼”问题的不同，运用“整体分组”等策略来解决。

在参与测试的82名四年级学生中，有17人能正确求解，约占总人数的20.73%，而约79.27%的学生未能正确解答。在初次测试中，能够正确解答的学生采用了列表法和分组法，而在未能正确求解的学生中，虽有部分学生也使用了分组法，但在应用过程中遇到了问题。尽管有学生尝试使用假设法，但结果并不正确。具体情况如下。

学生在掌握“鸡兔同笼”问题的求解方法后，会尝试用列表法求解“百僧百馍”问题，并得出正确答案。

使用假设法时，需要利用大和尚比小和尚多吃的馒头数进行计算。因为3-1/3=22/3（个），每个大和尚比每个小和尚多吃的馒头数是2/23个，不是整数个，而学生在分数的计算方面存在困难，常常不知道如何继续。

大约一半的学生想到了将大和尚和小和尚捆绑分组的策略。部分学生将1个大和尚和3个小和尚分为一组，从而求出正确答案。但学生遇到了以下问题：一是混淆捆绑对象，比如将1个大和尚、3个小和尚和4个馒头捆绑为一组，导致计算错误；二是即使分为了25组，也不清楚每组中大和尚和小和尚的数量，无法区分两者。这表明他们还不能熟练使用分组整体法来解决问题。

（二）设计铺垫题

为帮助学生解决难题、理解题意并突破难点，笔者根据学生的解题过程和“百僧百馍”问题的特点，设计了辅助教学的铺垫题。

1.破解假设法难点的铺垫题

学生在利用假设法求解“百僧百馍”问题时，会迁移“鸡兔同笼”问题的解题思路，把小和尚看成大和尚，但每个大和尚比每个小和尚多吃[223]个馒头，学生还未掌握分数加减法，更别提分数除法了。因此，笔者设计了假设法的铺垫题帮助学生破解难点。

【教学片段一】假设法的铺垫题

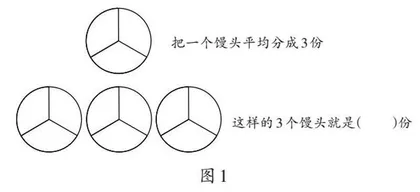
问题：观察图形，填一填（如图1）。

分析：把一个馒头平均分成3份，3个馒头就是9份，100个馒头就是300份，每把一个小和尚看成大和尚就多吃8份馒头，这样就可以把分数的问题转化成整数问题，再用假设法解题就简单多了。

2.破解整体法难点的铺垫题

四年级学生已经通过一些例子接触过整体法，例如已知三个数的总和与其中两个数的和，求第三个数，以及捆绑销售问题、行程问题中的相遇问题等。尽管如此，学生对用整体法解决问题的理解仍不够。例如在“百僧百馍”问题中，学生往往只考虑假设法，而忽略整体分组法。为此，笔者设计了铺垫题，以帮助学生更好地理解和运用整体思想来解决问题。

【教学片段二】整体法的铺垫题1

问题：笼子里有鸡和兔，共有96只脚，已知鸡和兔的数量相等，那么鸡和兔各有多少只？

分析：铺垫题中有鸡和兔脚的总数、鸡的数量等于兔的数量等条件，没有给出鸡和兔的总数。看到这样的条件，学生很可能会放弃假设法，而将1只鸡和1只兔捆绑成一组，每组中鸡的脚有2只、兔的脚有4只，共计6只脚。接着，用脚的总数除以每组的脚数，96÷6=16（组），得出共有16组。由于每组中只有1只鸡和1只兔，因此可以得出笼子里有16只鸡和16只兔。通过这个铺垫题，学生能够回忆起运用整体思想去思考和解决问题的方法，从而摆脱假设法的固有思维模式。

用整体法求解“百僧百馍”问题时，由于数据量大且复杂，学生又没有生活经验，所以易混淆。为此，笔者又设计了另一道铺垫题，立足现实生活经验帮助学生理解如何将事物视为整体进行分组，以便清晰解题。

【教学片段三】整体法的铺垫题2

问题：一家早餐店里每个菜包1元，每个肉包3元。一天，店里接到一笔订单，按每3个菜包和1个肉包装成一份进行配制，一共预订100个包子，这100个包子一共要多少钱？

分析：根据题意，将3个菜包和1个肉包装成一份，即3个菜包加上1个肉包共4个包子构成一组，100÷4=25（组）。每组包含3个菜包和1个肉包，共需支付6元，计算25组的总费用，即6×25=150（元），一共要150元。通过将菜包和肉包捆绑销售，连通“百僧百馍”问题，帮助学生理解用整体法解决问题的思路。

（三）第二次测试结果及分析

在学生独立完成上述的铺垫题后，笔者未进行任何形式的讲解，直接进行了难度较高的第二次测试，测试内容包括“百僧百馍”问题及其变式题。

【教学片段四】“百僧百馍”问题的变式题

问题：师傅做大小不同零件，做1个大零件需要3分钟，做3个小零件需要1分钟，王师傅花了80分钟，一共做了80个零件，王师傅做了几个大零件、几个小零件？

分析：变式题改变了问题的情境，但题目类型仍然相同，只要学生建立起“百僧百馍”问题的解题模型，遇到类似问题就能灵活解决。

1.计算正确率显著提高

正确解答“百僧百馍”问题的学生人数从首次测试的17人增加到57人，解题正确率从20.73%显著提高至69.51%。正确解决变式题的学生有45人，正确率为54.88%，其中有32人采用了分组法，占正确人数的71.11%。

2.解题方法趋向多样

在完成基础题目之后，使用列表法、整体分组法和假设法的学生均能正确解答。此外，还有部分学生采用画图法。

3.解题思路逐步明晰

有了铺垫题的过渡，学生在第二次测试时比第一次有了更清晰的理解。他们在面对问题时，不再盲目地尝试各种方法，而是能够根据铺垫题的提示，有针对性地选择解题方法。此外，学生在解题过程中也更加注重对题目信息的理解和分析，能够准确地把握问题的关键点，避免了因理解偏差而导致的错误。

部分学生第一次测试时答错了，而在第二次测试时计算正确，笔者选取两名学生的两次解答过程进行对比分析。

生1的两次解答过程见表1。在第一次测试中，生1也使用了分组的方法进行解答，却不明白把什么分成一组，把题目中所有出现过的和隐含的数据都加在一起作为一组，眉毛胡子一把抓。经过铺垫题的提示，在第二次测试中，生1厘清了应该把每个大和尚吃的3个馒头和每3个小和尚吃的1个馒头捆绑为一组。

生2的两次解答过程见表2。在第一次测试中，用分组法将1个大和尚和3个小和尚分为1组，算出一共有25组，但是以为25是小和尚的人数，而小和尚人数应该是3的倍数，所以想当然地直接在算式后面加上数字“2”得到“27”。在第二次测试中，生2能很清楚地表达计算过程，理解一共有25组，每组里面有1个大和尚和3个小和尚。

（四）第三次测试结果及分析

第二次的测试中，学生是不是因为对铺垫题的短时记忆才正确解答的呢？对此，笔者选择了在三个月后对学生进行第三次测试，结果显示正确率为60.98%，明显高于第一次测试正确率，说明学生脑中已经建立起了“百僧百馍”问题的解题模型。

四、研究启示

从教学实践中可以发现，学生可以从铺垫题中逐步发现解决问题的方法，同时也发现一些问题。

首先，部分学生的思维模式较为封闭，灵活性有待提高。

通过上述三次测试可知，仍有30%-40%的学生不能正确解决这个问题，究其原因是部分学生不会针对题目的特点灵活选择合适的方法，思考问题时拘泥于一个方向，即便看到前方是个“死胡同”也不回头，而是想通过“凿墙”找到“出路”，未能从多角度探索其他可能的解题途径。因此，教师应加强对学生思维灵活性的训练，以培养其发散思维的能力。

其次，教师应深入理解学生解题思维，设计有效的教学铺垫。

测试显示，学生独立完成铺垫题有助于他们解决“百僧百馍”问题，提高他们的解题效率。铺垫题的设计应基于学生认知水平，教师需要分析学生的理解程度，识别解题难点，挑选易于理解的解题策略来设计题目。这样，学生能利用已有认知逐步掌握新的解题方法。学生通过自我解题、思考和反思，能发现最佳解题路径，提升解题能力和培养核心素养。

［ 参 考 文 献 ］

[1] 张高淞.关注问题的解决，聚焦策略和数学思想：以“百僧百馍”一题为例[J].数学教学通讯，2022（1）：70-72.

[2] 蒋燕芬.分析难点   设计铺垫   提升能力：高段学生解决一个几何问题的研究[J].教学月刊小学版（数学），2023（5）：50-54.

[3] 盘梦婕.百僧分馍[J].学苑创造（3-6年级阅读），2016（Z2）：60.

[4] 陈连玉.百僧吃九十二馍如何：“百僧吃百馍”分组法解答的再思考[J].新教师，2016（2）：77.

[5] 陈祥.百僧分百馒问题解法举隅[J].数学小灵通，2002（Z2）：63-64.

[6] 洪国镛.用分组法巧解“古算题”[J].小学教学研究，2002（4）：25-26.

（责编    杨偲培）