浅谈“激励”在教学中的作用

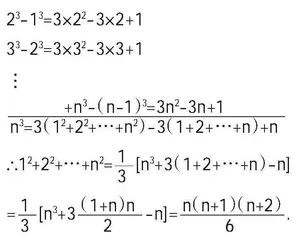
摘   要：在课堂上教师的“激励”会形成皮格马利翁效应，帮助挖掘学生自主探究、独立思考的积极性，以及对待挑战问题的执着和热情。通过在教学中合理的利用激励教学，教师可以帮助学生更好地认识世界，更加有效地实现他们的学业目标，达到凡为教，目的在于达到不需要教的教育理念。

关键词：中学数学;激励教育;皮格马利翁效应

中图分类号：G633.6   文献标识码：A    文章编号：1009-010X（2025）02-0035-03

“激励”旨在通过激励、鼓励和督促的方式让学生更有信心和勇气去实现他们的梦想。激励教育是将“在激励中学习，在激励中成长”的理念融入到课堂中，帮助学生更好地认识世界，更加有效地实现他们的学业目标，并且提高他们的使命感和进取心。在“教是为了不教”的课堂上，要想让学生真正掌握知识，就必须让他们主动思考，而非仅仅依赖于教师的传授。为此，需要采取多样化的措施来唤醒他们的学习热情，以及利用外部环境来促使他们的思维活跃起来，从而培养他们的创新思维和实践能力，以达到“教是为了不教”的学习效果。

通过课堂实例，讲述笔者实施“激励”教学的方法。如，在教学选择性必修第二册“数学归纳法”时，教师讲解课本47页的例2：

用数学归纳法证明：

证明：（1）当n=1时，①式的左边=12=1，

所以①式成立。

（2）假设当n=k（k∈N*）时，①式成立，即

在上式两边同时加上（k+1）2，有

即当n=k+1时，①式也成立。

由（1）（2）可知，①式对任何k∈N*都成立。

讲完例题后，何XX同学举手问了一个问题：“老师，正整数的平方和公式，如果不是证明题，这个公式该怎么推导出来呢？”换做平时，笔者肯定就直接说：“这个不是本节课的重点，属于了解内容，会用数学归纳法证明，记住结论就可以了”。但这节课是在英才班开展的教学，学生数学基础好，思维活跃，喜欢钻研，乐于探究，对课本中的一些细枝末节总能发现并提出一些意外问题。于是笔者没有回避学生提问，却也不想直接告诉公式来源，考虑到公式本身推导不难，而学生们数学素养都很高，所以笔者转换了处理方式，说道“何XX同学提出一个很好的很值得研究的问题。我作为老师也很少关注这个问题，其实这个公式的推导我只知道一个方法，就是数学归纳法，其他的方法不知道。但我相信你们能研究出来，因为在座的同学们都有很好的数学功底和数学素养，所以我布置一个思考作业，就是用我们学过的数列知识研究推导这个公式，要求独立探索求证，希望同学们发挥自己的聪明才智，在明天的课堂上展示自己的研究成果，我临时当个评委，看看谁的证明最简练、最漂亮，希望我能表扬到你啊，好好准备，期待明天！”笔者用示弱和激励的办法，鼓励学生们去自主探究，通过已经掌握的数列知识，经过独立思考，最终证得公式，体验到问题解决后的成功喜悦。

皮格马利翁效应是一种深刻的社会心理现象，“你期望什么，你就会得到什么，你得到的不是你想要的，而是你期待的。” 笔者期待着第二天的课堂出现皮格马利翁效应。它暗示着教师的期望可以以出人意料的方式实现，从而产生出意想不到的效果。

第二天课堂上同学们准备得很充分，主动、热情地展示了自己的研究结果，证法精彩纷呈，讲解头头是道，充分享受到讲解的快乐和成功的喜悦。笔者作为评委，评选出了最好的三位同学的方法。

第一种是何XX同学的证法：

第二种是范XX同学的证法，他当时讲解时自信满满，证明的方法也很特别：他把求和变成一个“范XX三角”，转换了两次顶点形成三个数字三角形，如下示所示：

第一行相加=n（2n+1）

第二行相加=（n-1）（2n+1）

第三行相加=（n-2）（2n+1）

第n行相加=1（2n+1）

第三个是吴XX同学的证法，讲之前学生就提到自己的方法比其他同学更简单，只用了一个立方差公式：

∵n3-（n-1）3=n2+n（n-1）+（n-1）2=3n2-3n+1，

∴13-03=3×12-3×1+1

看着学生们一个比一个精彩的展示，笔者感慨万千，英才班有这么多优秀的学生去认真探究了这个问题，把教师留的思考题当成一个挑战，积极主动地去想办法解决它，争着比着看谁的方法更出色！这种可喜的结局令人振奋，这是一群不能小觑的优秀学生，他们体现出来的钻研精神和创造力远超出老师的想象。“皮格马利翁效应”提供的观点可谓深刻：鼓舞、肯定、相互信赖与期许，都深深影响着个体的发展。如果一个人受到其他人的肯定、认可，就能够更加坚定地追求自己的目标，拥有更多的活力去实现更大的梦想，不断地满足别人的需求，让大家都受益匪浅，让社会的认可更加牢固。

一次关于激励的课堂，使笔者受益良多，更加清楚地认识到，在教育的进程中，学生是一个独立的个体，他们拥有思考、表达、探索的权利，而老师的讲授无法完全满足他们的需求，唯一的办法就是利用外界的环境，引导他们去思考、去探究，勇于挑战、勇于创新、勇于提出问题、勇于进行反思，并且与他人进行沟通、互相批判，从而最终掌握所需的知识。通过深入思考和实践，我们可以获得更多的知识，并有效地实现“凡为教，目的在于达到不需要教”中叶圣陶先生的理念。