基于儿童视角促进数学思维发展

“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学。"数学作为一门重要的基础学科，怎样让小学生喜欢它，是我一直思考的问题。数学教学，是数学活动的教学，师生在活动中探索、在活动中发展。数学活动，一是个人的活动，比如，描一描、画一画、折一折、拼一拼、搭一搭;二是小组之间的交流、合作、探究活动。在教学中，我致力以儿童的视角引导学生探究、发现并解决数学问题

一、基于儿童视角，直观体验，让数学思维变得可触及

例如，北师大版四年级上册“不相邻单位之间的进率”，主要考查学生的单位意识。有这样一道填空题：个100是一万，十万里面有个1000，一亿里面有个10000。对于这道题，学生往往不能很好地把文字叙述和数字叙述联系起来，经常出错。我在教学中是这样引导的：（1）转化，引导学生把语言叙述的一万换成数字的表示方法10000。（2）找等量关系，个100是10000，等量关系是× 1 0 0=1 0 0 0 0 ，十万里面有个1000则是100000里面有个1000，等量关系是 1 0 0 0 0 0 ÷ （ σ ） = 1 0 0 0 。通过转化，文字转化成数字，再找出等量关系，直观简洁，学生一目了然，问题迎刃而解。

再如折绳问题：一根绳子对折，再对折，第三次对折后，从中间剪断，共剪成多少段？这道题，不少学生都感觉无从下手，我先引导大家折一折，剪断数一数，又让大家画一画，通过两种方法都能判断出剪成了9段。再结合直观图操作，引导学生观察、推理、总结，得出结论：剪后绳子的段数正好比切口多1。

二、基于儿童视角，强化语言表达，发展思维能力

语言是思维的外壳。课堂上，我们要创设宽松、和谐的氛围，引导学生敢说敢讲，表达观点，促进学生思维能力、思辨能力的发展。

例如，树上飞来5只鸟，又飞走3只鸟，现在有17只，原来有多少只鸟？列式为 + 5 - 3 = 1 7 。这里把“ + 5 ”看作一个整体，逆推就变成了多少减去3等于17，因为20减去3等于17，所以 + 5 = 20。这样就引导学生理解了“ .。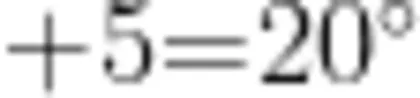

引导学生用自己的语言说一说解题的过程，这样既能发展学生的语言表达能力，又能渗透整体性思维、逆推思维，逐步提升学生的数学思维能力。

三、基于儿童视角，打破思维常规，数形结合发展思维能力

如填空题：

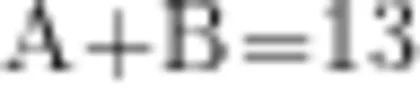A + B ÷ 3 = 7 ，求 B - A= （

对这道题，学生到五年级学习分数之后也不难解决，但对于三年级学生来说，按照常规思维解决该题还是有难度的。我引导学生借助数形结合的方法来分析这道题。把B÷3看作一个整体，画图如下：

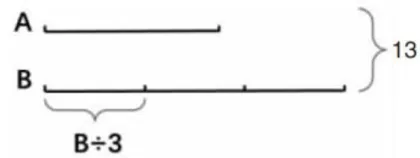
由已知条件和图示得： 2 × （ B÷ 3 ） = 1 3 - 7 = 6 所以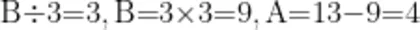， 业

所以： B - A= （ 5 ） 。

再如：6个空瓶换1瓶水，买120瓶，实际能喝几瓶水？

这是一个经典的逻辑思维和数学实际应用问题，想要得到最优化决策，只有打破常规思维，从多个角度思考。

解法一：转化法。

把6个空瓶转化成1个空瓶 + 1 份水。因为：6（ 8 ） = 1 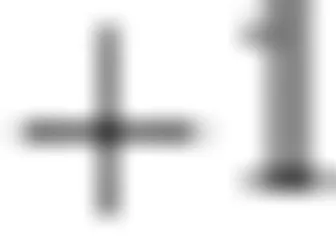份水

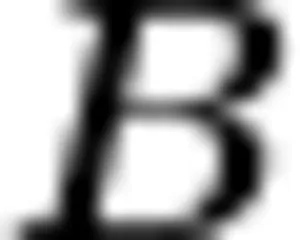所以：5（ ） 份水

1 2 0 + 1 2 0 ÷ 5 = 1 4 4 （瓶）

解法二：借来还去法。向老板借来1个瓶子，最后再还回去。1 2 0 ÷ 6 = 2 0 （瓶）2 0 ÷ 6 = 3 （瓶）···2（瓶）3 + 2 + 1 （借） = 1 （瓶）1 2 0 + 2 0 + 3 + 1 = 1 4 4 （瓶）

四、基于儿童视角，引导建模，拓展思维能力

同一道题，不同年级，我会根据学生特点需要采用适合的方法。在二年级借助图示直观解题的基础上，逐步到四年级的线段图，到五、六年级抽象为典型的盈亏问题。学生通过实际问题抽象为数学模型，学会将复杂问题简化为基本问题来处理，形成模型思想。模型思想的建立不是一朝一夕的，它是在学生思维发展的基础上逐步构建的知识体系。

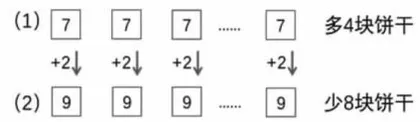
例如，幼儿园给小朋友分饼干，如果每人分7块，就多4块，如果每人分9块，就少8块，那么一共有多少小朋友？

二年级：直观解题。

两种方案正好差 4 + 8 = 1 2 （块），相差的

12块正好是每个小朋友多拿的2块，所

以： 1 2 ÷ （ 9 - 7 ） = 1 2 ÷ 2 = 6 （个）。四年级：半抽象，线段图。

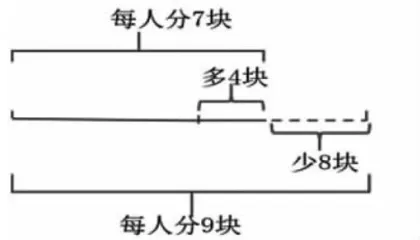
（ 4 + 8 ） ÷ （ 9 - 7 ） = 1 2 ÷ 2 = 6 （个）。五年级或六年级：抽象，公式法。（盈 + 亏） ÷ 分配差 σ= σ 份数。（ 4 + 8 ） ÷ （ 9 - 7 ） = 1 2 ÷ 2 = 6 （个）。所以，在教学中，我们要结合实际灵活解决问题。

五、基于儿童视角，理解数学本质，深化思维能力

如，甲+乙 = 6 1 ，甲 ÷ 4 + 7 ÷ 5 = 1 4 ，甲 Σ= Σ ），乙=。

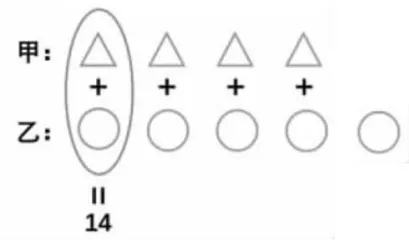
因为 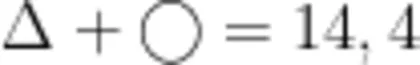个（ ： Δ + Δ ）是：1 4 × 4 = 5 6 所以 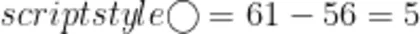乙： 5 × 5 = 2 5 甲： 6 1 - 2 5 = 3 6 解决本题的关键是要抓住数学的本质，除法的本质就是平均分，然后再用整体思想分析、解决问题，从而提升学生的思维能力。

总之，学生思维品质的培养和发展离不开教师的点拨与启迪。在教学中，我们要善于站在儿童的视角思考问题，让学生充分享受数学带来的乐趣，从而爱数学、用数学，有效提高数学思维能力和学科核心素养。

（责编 佳琪）