数学课堂因“问题”而不凡

《义务教育数学课程标准（2022版）》指出：要引导学生在发现问题、提出问题的同时，会用数学的眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界。可见，数学课堂的心脏是“核心问题”。核心问题的有效实施，有利于教与学的提质增效，真正实现课堂教学的高效性。教师以“核心问题”为主线，引导学生经历独立探索、小组合作等多种学习方式，深刻理解知识和掌握思想方法，有助于提升课堂教学效率，锻炼学生思维，激发学生自主学习的能力，培养数学核心素养。

一、紧扣情境，提出核心问题

在教学中，教师借助真实情境提出问题，引导学生围绕问题进行深入思考、分析、探究。学生能更主动寻找解决问题的路径和方法，进而提升自主学习能力。在“认识小数”（三年级下册）的前测中，了解到学生虽然在生活中对“小数"有所接触，但并未真正了解小数的含义。因此，依据生活情境的角度巧设核心问题，能有效激活学生的学习内驱力，使更多的学生主动卷入到学习中。因此，在“认识小数"伊始，教者设计了小朋友坐公交车免票身高调整的情境：“在以前，身高不超过1.1m 的可以免费乘坐公交；随着社会发展，小朋友的身高普遍增高。2011年后，调整为身高不超过 1.2m 的可以免费乘坐，相比以前提高了0.1m 。”教师根据具体情境提出4 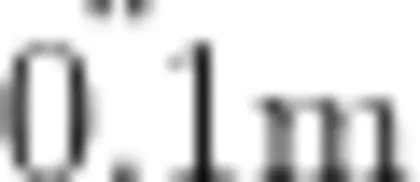究竟有多长？ 0.1m 与 1m 有什么关系呢？”等问题，让学生从已有生活经验出发，表达并分享对0.1m 的见解。“是多长？”这个问题是启动学生调动已有的米制经验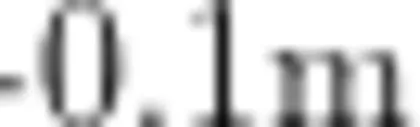， 与 1m 是什么关系”则是揭示小数是十进分数的实质。以核心问题推进课程，逐步引导学生探究小数的知识。这不仅贴合学生的认知规律，更凸显小数与日常生活的紧密联系，有助于学生深刻感受小数的实际应用价值。

二、联接旧知，提出核心问题

“比例的意义”的学习基础是比的意义、求比值、比的基本性质等知识。比例与比存在密切的内在联系。通过“比”引进“比例的意义”，让学生带着核心问题去探究和理解“比例的意义”，使学生全身心地沉浸在学习过程里。因此，在教学时，结合“比”的知识设计以下核心问题：1.求比值，探规律。通过求比值，调动学生已有的“比”的知识经验，再通过观察发现：第一组三个比的比值相等，因此得知第一组图形的大小不同、形状相同；第二组三个比的比值不相等，第二组图形大小、形状都不相同。为学生挖掘比例概念的内涵做好铺垫。2.归纳概括，理解概念。教学时，学生以真问题“什么叫作比例”为研究核心，经历“写比、求比值—发现规律—表示规律—揭示概念”过程。学生的思维在有限的课堂学习时间内尽可能延伸，理解比与比例之间的内在联系与显著差异。

三、抓住本质，提出核心问题

例如，《正比例》这节课，笔者备课时思考：正比例的核心本质是什么？抓住什么就能帮助学生真正理解正比例的意义？在帮助学生建立“正比例，概念表象时，是让学生机械记忆结论重要，还是引导学生深入探究变量之间变化关系的过程更有意义呢？经过研读教参、教材和反复推敲，发现：后者更为重要。如果学生能够对两种变量之间的变化规律有足够深刻的认识与理解，那么“正比例"这一数学模型自然在学生心中生根发芽。基于以上思考，笔者围绕“相关联的量”和“比值一定”设计了两个核心问题，并设计相应的学习任务，让学生在真实的问题情境中理解变量，深入领会“正比例”的意义，提升思维的深度和广度。课始，学生感悟相关联的量后，设计相关的学习任务，在引导学生探究“相关联的量”这个核心问题前，教师抛出学习任务，明确探究要求。学生通过几个材料的对比和辨析，发现异同之处，初步体会“正比例"的意义。由此揭示正比例关系的第一个核心问题：两种相关联的量的变化规律是正比例的本质。引导学生从整体的角度去认识和理解正比例，有助于他们深入把握这一数学模型的精髓。在理解“相关联的量"后，让学生根据三个表的变化情况继续补充表格，发现其中的规律，学会用“函数”的眼光去理解数量关系中量与量的变化规律，深入理解正比例的意义。“正比例”这节课是学生首次从变量的视角出发，深入探究两个量之间的关系，实现从“数量”的简单理解到“关系”的深度探索的跃迁，是学生学习函数的重要基础和重要契机。核心问题“如何判断两种量是否成正比例关系”，为正比例概念的形成和内化提供有力的支撑。在它的引领下，学生的核心素养逐渐提高。

责任编辑 徐国坚