深度学习：将数学思想方法渗透课堂

清代袁枚在《续诗品·尚识》中指出：“学如弓弩，才如箭鏃，识以领之，方能中鹄。"这里的“学"指知识，“才”指方法，“识"指思想。思想与方法之间存在紧密的联系，数学作为一种推理和运算的工具，本质上代表一种方法：一方面，数学思想方法依托于数学知识，如果脱离了知识的传授，思想方法便失去了根基，如同"无本之木、无源之水”；另一方面，教师应引导学生在有效探究的过程中，领悟知识背后支撑的方法和蕴含的丰富思想。教师要结合具体情境，引导学生领悟这些思想，让学生顺利将新知识融入自身认知结构。因此，教师不仅要传授数学知识，而且要融人数学思想方法，使学生能够运用数学思想认识世界。

在实际的教学过程中，部分教师常常只关注知识的教学，忽视了数学概念、性质、法则、公式等体现的数学思想方法，导致学生对知识的掌握变得单一且肤浅，无法深入核心层面，难以彰显学科的本质。下面，笔者通过几个实例来分析在教学中渗透数学思想方法可能遇到的误区，并探讨相应的解决策略。

一、误区一：错过策略的生成点， 浅尝思想

案例：在教学“面积的含义"时，教师在探讨面积大小比较的环节中展示了数学书、体育书、音乐书、故事书、美术书。教师要求学生选择其中两本书，比较它们封面的面积大小。

教师提出要求后，学生满怀热情地开始比较和讨论。两分钟后，他们开始汇报。

师：谁来说一说，你选择的是哪两本书？

生1：我选的是体育书和美术书，体育书封面比美术书封面的面积小。

师：你用的是什么方法？

生1：我用的是观察法，美术书封面的面积比体育书封面的面积大多了，所以一眼就能看出来。

生2：我选的是音乐书和数学书，数学书封面比音乐书封面的面积大。把这两本书重叠在一起，便能比较它们封面面积的大小。

师：还有比较其他书封面面积的吗？

生3：我比较的是美术书与故事书的封面，美术书封面的面积更大。

师：下面请同学们比一比美术书封面和数学书封面的面积，哪个大，哪个小？

（在汇报过程中，学生的意见出现分歧）

师：看来用观察法和重叠法无法准确比较美术书封面与数学书封面的面积大小。你们能否提出一个让所有人都信服的方法呢？（在教材中，关于面积概念的教学被安排在引入面积单位之前，学生尚未接触过面积单位，因此这里为新知识的教学埋下伏笔，激发学生探究面积单位的兴趣）

（教师原以为这个问题无人能解，突然，学生4站了起来）

生4：老师，我找到了解决方法。我们可以把不重叠的部分剪下来比一比，如果比不出来，再把不重叠的部分剪下来比一比，直到比出来为止。

教师一愣，意识到这种方法是正确的。然而，为了追赶教学进度，教师仅对这种方法进行简单评价：“这种方法是可行的，下课后可以试一试。”这样，就会失去深入渗透转化思想的最佳时机。

教学诊断：由于教师没有精心准备教学内容，无法预料生4能得出上述答案，未能深入挖掘隐藏在答案背后的思想方法，因此用“下课后试一试"来敷衍。本课旨在培养学生的面积感知能力，使他们理解当无法直接比较大面积单位的大小时，可以通过更小的面积单位来进行比较，从而实现更精确的比较。教师要为学生自主学习提供扩展和延伸的课外平台，以便学生在课余时间能够进一步拓宽视野。如果教师忽视那些对学生成长至关重要的数学思想方法，那么就偏离了课程改革的初衷。

对策一：精心挖掘教材深处的思想。

教材是教学活动的主要媒介。教材的价值体现在两个方面：一是数学知识，这些知识明确地呈现在教材中，将它称为显性价值；二是数学思想方法，这些思想方法蕴含在知识体系之内，将它称为隐性价值。因此，在进行教学设计时，首先，教师要更新教育观念，重视并开发教材的隐性价值，将思想方法的教学融入教学目标；其次，教师应深入研究教材，积极挖掘可以用于思想方法教学的元素，并将这些思想融入知识传授的具体教学环节中；最后，教师应根据学生的年龄特征和认知水平决定如何在具体内容中渗透思想方法，以及渗透的深度。

对策二：关注思想，深化学生的量感体验。

作为充满活力的个体，学生带着自己的知识、经验和情感进行对话、交流和思考。即使教师的预案设计得再周全，也无法与现实情境完全吻合，因为学生的思维中蕴含着难以预料的元素。当预设的情境未能如愿出现时，教师应顺应课堂的动态变化，为学生创造自主感悟、领悟和实践的机会。教师不仅要俯下身来耐心倾听学生对问题的理解，清晰把握学生的心声，还应引导学生运用多种方法来测量面积，加深对度量的理解。

二、误区二：注重解题思路，忽略思想

案例：某教师在教学“三角形的面积计算"时，怕学生发现不了三角形面积计算方法，因此做了精心的铺垫。教师先展示一个平行四边形、一个长方形和一个正方形，引导学生回顾这三个图形面积公式的推导过程；然后，呈现图1。

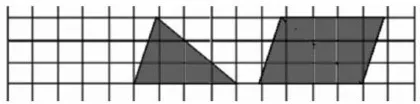
师：图1中每个小方格代表1平方厘米。你们能计算出涂色的三角形和平行四边形的面积各是多少平方厘米吗？（学生开始数方格，教师在巡视中提供指导，随后各小组汇报他们的发现）

生1：我们组得出的结果是三角形的面积为6平方厘米，平行四边形的面积为12平方厘米。

师：猜一猜，平行四边形面积和三角形面积有什么样的关系？

生2：平行四边形面积是三角形面积的两倍。

师：他的猜测是否正确呢？请同学们拿出课前准备的两个完全相同的三角形拼接一下。

学生仅用几秒钟便迅速拼接出一个平行四边形。最后，教师引导学生比较拼出的平行四边形与三角形的底、高以及面积，从而顺利推导出三角形的面积公式。

教学诊断：乍一看，上面的教学过程似乎畅通无阻，教师的设计显得无懈可击。实际上，学生仅是在教师的暗示和铺垫下“走过场”，被教师引导着演绎了一场早已导演好的戏。“操作需要探究性，这样才有意义和学习的价值。"（顾汝佐语）在这节课中，学生思维的局限性体现在是否有将三角形转换为平行四边形的观念，以及掌握转换的策略。复习平行四边形的面积公式推导过程并引入新课程的目的是为了渗透转化思想，然而这只是教师的主观意图，学生未能发现新旧知识之间的联系。教师在引导学生观察平行四边形与等底等高的三角形后，鼓励学生猜想平行四边形面积和三角形面积的关系，学生不用推理便能直接回答，这样的猜想与教师直接告知并无差别。

对策一：抓住核心问题，启动项目化学习。

数学思想方法的渗透难以用言语表达，教师如果直接传授，学生将无法体验思想的形成过程。教师要聚焦关键问题，编织一条线索，引导学生自行探索，点燃他们思维的火花，使他们真正成为学习的主人。如此一来，学生便能在探索的过程中领悟数学思想与方法，并在掌握新知识的过程中体验成功的喜悦。比如，在前述案例中，教师可以通过提问“关于三角形，你们已经掌握了哪些知识”，激发小组成员开展自由讨论。然后，教师可以邀请学生扮演“小老师”，讲解三角形面积公式的推导过程。在教学长方形、正方形以及平行四边形的面积时，教师逐步引入转化思想方法。因此，当学生尝试推导三角形面积公式时，他们很自然地想到运用转化思想。在教学过程中，教师应当勇于放手，让学生自主探索，参与项目化的学习活动，设计贴近真实情境的任务，促使学生综合运用所学知识解决实际问题。

对策二：循序渐进，迎难而上领悟思想。

教师应依据课堂的动态变化，精准地找到合适的时机引入挑战，激发学生的求知欲，为课堂注入活力，让学生在学习过程中体验数学文化的熏陶与影响。教师要通过设置适度的障碍，让学生经历“跳一跳摘桃子”的过程，激发学生的学习热情。在努力“摘取桃子"的过程中，学生会体验困惑、深思和顿悟，这些宝贵的经历将成为他们难忘的记忆。

三、误区三：思想模块零碎，无法体系化

案例：一些教师会将整体知识拆解为众多分散的知识点，并逐一进行教学。虽然这种做法能够加深学生对每个知识点的理解，但是无形中将原本连贯的知识体系拆解得支离破碎。教师如果只专注于逐个突破知识点，而忽视渗透相应的思想方法，学生的知识结构将会变得杂乱无章，难以构建完整的知识体系。这样一来，学生在应用知识时会感到迷茫，不知从何下手，最终导致学习效率低下、事倍功半。

对策一：重视模块教学，整合思想体系。

深刻理解数学知识结构体系及其内涵，关键在于认识和掌握数学的思想方法。小学数学涵盖三个主要领域：数与代数、空间与图形、统计与概率，在每个领域都有若干核心思想方法将各个知识点紧密联系起来。比如，数与代数领域的认数模块渗透了数形结合思想和集合思想，加法计算是并集思想的载体，减法计算是差集思想的载体，乘法计算由几个相同加数相加计算转化而来，除法计算由乘法计算转化而来。因此，在教学某一模块知识点后，教师应鼓励学生逐一梳理该模块相关的知识内容和所运用的思想方法，总结基本概念、法则、公式，回顾知识的发现过程，明确知识点之间的内在联系，并尝试构建本模块的知识网络。

对策二：学进去“思想”，讲出来“方法”。

数学思想方法的渗透不可能通过一次练习就一蹴而就，因此，在教学某一知识点时，教师应多次进行渗透，让学生反复体验，从而内化知识。此外，教师提供类似案例让学生进行进一步研究，有助于深化学生对这些思想方法的理解。然而，对于深入理解思想方法而言，学生只掌握微观教材是不够的。因此，在教学过程中，教师不仅要指导学生通过反复练习知识点来领悟思想方法，还要引导他们跳出这一知识点的局限，从宏观角度审视教材。只有这样，教师才能将学生“领人"深人挖掘思想的境界，然后再带他们"走出”，促进他们梳理知识的整体脉络，真正理解教师的教学意图。

总之，数学思想方法是数学学科的精髓，也是数学素养的关键要素。教师要引导学生自主探索知识、进行小组合作，亲身体验和感悟概念的形成、公式的推导以及法则的制定过程，让学生掌握必要的数学思想方法。这样，学生的数学思维才能得以优化，数学精神才能得以树立，从而实现从“学会数学"到“会学数学"的质的飞跃。