理解旋转本质 发展空间观念
作者: 董余微“图形的旋转”是“图形与几何”板块中重要的教学内容。在教学时教师既要关注新旧知识的联系,又要用原有知识促进新知识的形成。因此,笔者在本节课的设计中更加注重想象操作与数学思维的结合,通过引导学生运用转化的方法,深化学生对图形运动的拓展延伸,为学生后续学习打下坚实的基础。
一、纵横联系,分析核心内容
纵观人教版教材,小学阶段关于图形运动的教学分为三个阶段。
图形的运动(一):在二年级下册,主要内容是认识平移、旋转及轴对称现象。
图形的运动(二):在四年级下册,主要让学生通过观察、操作等活动进一步认识平移和轴对称。
图形的运动(三):在五年级下册,主要让学生从定量的角度去分析和学习图形的旋转。
横向对比人教版、北师大版、苏教版三个版本的小学数学教材,笔者发现:虽然选择的素材不相同,但都是以“明确三要素一感知旋转特征—会用旋转画图”的路径进行教学;三个版本的教材都借助实物让学生通过画图突破难点,理解旋转运动的本质是“点的运动”。
二、学情调研,把握学习起点
为了更好地研究学生、读懂学生,更准确地把握学生的学习起点,做到顺学而导,笔者对学校五年级3个班的学生进行了前测。
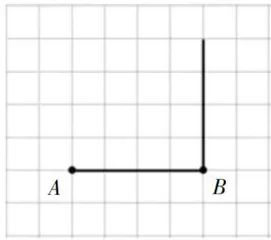
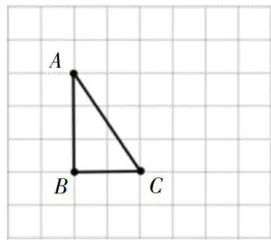
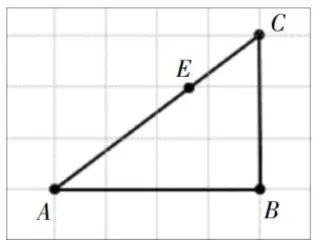
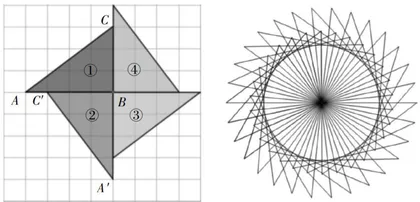
前测题1:写一写,如图1,请描述线段 A B 是怎么旋转的?
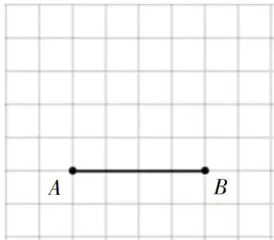
前测题2:画一画,如图2,请在方格纸上画出线段 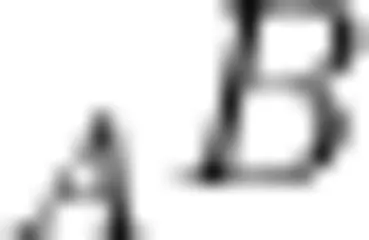 绕点 B 顺时针旋转90后的图形。
绕点 B 顺时针旋转90后的图形。
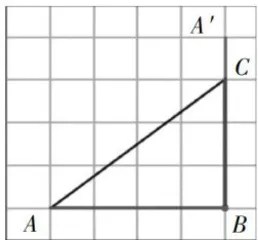
前测题3:画一画,如图3,请在方格纸上画出三角形 A B C 绕点 B 顺时针旋转 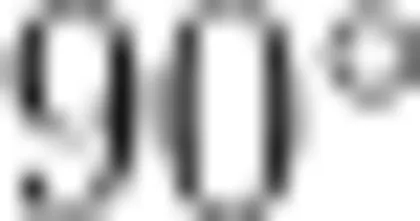 后的图形。
后的图形。
笔者对前测结果进行统计与分析后发现:学生对旋转过程的语言描述不完整,能用三要素合理描述图形旋转的学生仅占 15.7% ;学生画线段旋转的正确率较高,但学生面对旋转制图普遍存在困难。基于学情分析,笔者提出两点优化建议:一是教师要重视数学语言表征旋转的过程与结果,通过“三要素”的对比感悟,引导学生把元认知不规范语言转化为数学语言,以提升学生的几何思维水平;二是引导学生打通点、线、面三者旋转过程的一致性,让学生理解旋转的本质就是点的运动。
三、重组思考,统整学习内容
1.学材调整
首先,将钟面改换成线段。钟面的中心点只有一个,不易形成对比。指针通常只沿顺时针一个方向旋转,学生感悟到的旋转含义不够深刻。教师可以将线段作为主要学材,以有效突破“旋转三要素"及画图的教学难点。
其次,教师可以通过增加线段与三角形上点的旋转来突破教学难点,促进学生对旋转本质的理解。
2.内容整合
教师可以对图形的旋转进行整体思考,将旋转特征融入线段旋转与三角形旋转的教学过程中。在教学中教师可以将平面图形的旋转化归为线段的旋转,线段的旋转化归为点的旋转,进而化解画平面图形旋转的难点。
3.整体关联
教师要聚焦图形旋转运动的本质,重视沟通三种运动方式的一致性;要增加三种运动方式的对比联系与应用,完善图形运动知识的结构,深化对图形运动的拓展延伸。
四、整体架构,促结构化学习
教学内容的结构化是实现整体教学的关键,设计结构化的材料是内容结构化的重中之重。笔者从纵向结构化和横向结构化两大策略出发进行素材的创编:纵向设计了一组从局部到整体、从一维线段旋转到二维三角形旋转的进阶性学材;横向设计了轴对称运动、平移运动和旋转运动进行比较的关联性学材,让学生有关联地学,打通点、线、面三者旋转过程的一致性,理解旋转的本质就是点的运动,进而实现整体性地学。

整节课教师利用三组材料设计了三个活动,实现了两次转化,即将面转化为线、线转化为点。
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:sxjz20250304.pd原版全文
活动1:如图4,画出线段  旋转
旋转 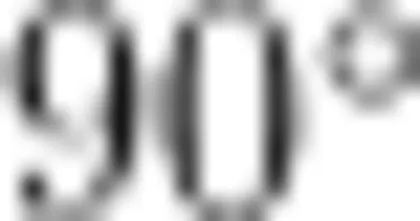 后的图形,并想象线段上点的运动。
后的图形,并想象线段上点的运动。
活动2:如图5,想象半成品三角形 A B C 绕点 B 顺时针旋转 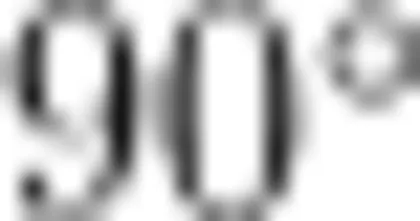 后的图形。
后的图形。
活动3:如图6,画出三角形 A B C 及点 E 绕点 B 逆时针旋转 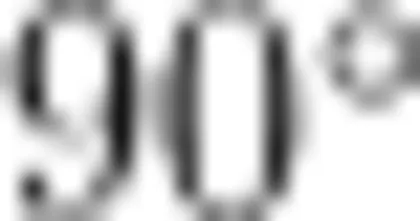 后的图形。
后的图形。
1.纵向结构化,实现进阶性学习
(1)从整体到局部
教师通过动态演示三角形旋转的过程,唤醒学生对旋转现象的认知,将研究复杂的图案转化为研究一个三角形的旋转,再聚焦到三角形的一条边开始研究。从整体到局部,渗透化繁为简的数学思想。
师:仔细观察,如图7,图案是怎么形成的?
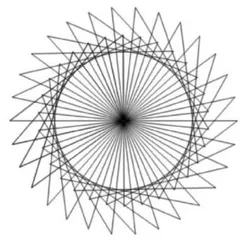
生1:它是三角形一直旋转得到的。
师:旋转是图形的一种重要的运动方式。如果三角形的一条边,线段AB旋转了一下,会得到怎样的图形呢?全班同学想象到的是不是相同的图形?
生2:不是,有的旋转的角度大一些,有的旋转的角度小一些。
生3:旋转角度不同,旋转后的图形也会不同。
师:是不是只要旋转角度相同,旋转后的图形就会一样?
教师出示活动1要求:请画出线段  旋转
旋转 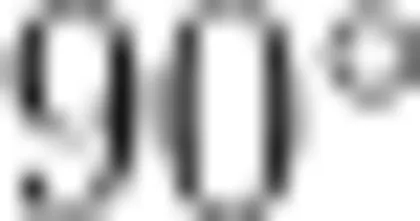 后的图形。
后的图形。
师:如图8,这几幅同学的作品都是旋转90吗?为什么结果不一样?
生4:方向不一样,有的是向下旋转的,有的是向上旋转的。

生5:有些是顺时针旋转的,有些是逆时针旋转的。
师:与钟表上时针旋转方向一样的叫顺时针方向,与时针旋转方向相反的叫逆时针方向。看来旋转方向是影响旋转的一个重要因素。
教师根据学生回答板书:旋转角度、顺时针、逆时针、旋转方向。
师:这两位同学的作品都是顺时针旋转  ,为什么旋转结果还是不同?
,为什么旋转结果还是不同?
生6: ① 是绕A点旋转的, ③ 是绕 B 点旋转的。
师:图形旋转时绕的点叫作旋转中心。(板书:旋转中心)
师:是不是有了旋转中心、旋转方向和旋转角度就能准确描述旋转了呢?
教师板书:线段  绕点 B 顺时针旋转
绕点 B 顺时针旋转 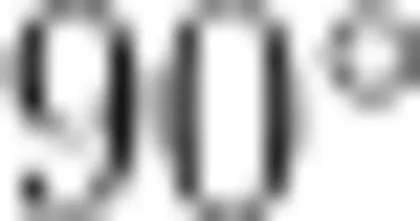 0
0
生7:确定了旋转中心、旋转方向和旋转角度,只有一幅图符合情况
师:所以在数学上我们就把旋转中心、旋转方向和旋转角度称为旋转三要素。(板书:旋转三要素)
(2)从局部到整体
为了帮助学生突破画图的难点,在已经确定一条关键线段旋转后位置的基础上,教师引导学生利用三角形的两条边进行旋转,从线段的旋转自然过渡到三角形的旋转,让学生通过想象探讨将面的旋转转化为找关键线段的旋转。
师:根据线段 A B 旋转后的位置,请你们想象三角形 A B C 绕点 B 顺时针旋转 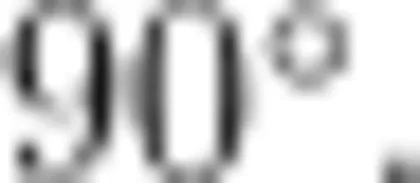 后的位置。
后的位置。
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:sxjz20250304.pd原版全文