基于思维发展 设计数学教学

数学思维既是学生认识数学的工具，又是学生掌握数学的武器。核心素养背景下的数学教学应将培养学生思维能力放在首要位置。实践证明，重视学生思维发展的课堂，可促使学生实现客观知识与主观意识间的平衡，从而让学生更好地发现问题、提出问题。教师应基于学生思维发展的视角设计教学活动，引导学生在活动中发展思维和提升学力。笔者以“圆的面积"为例，探讨如何基于学生的思维发展设计教学过程。

一、教学简录

1.情境创设，揭示研究主题

教师借助多媒体播放一只羊的活动视频。画面中，一只被拴着的羊，转了一圈又一圈。

师：请用数学的眼光分析，由这段视频想到了什么？

大部分学生想到了圆，以拴羊的木桩为圆心，绳子就是该圆的半径；有的学生从羊转了一圈又一圈想到了圆的周长。

师：关于圆的周长计算，大家都不陌生。该圆的面积是什么呢？

生1：该圆的面积就是羊的活动范围。

师：很好！如果想让这只羊吃到更多的草，就需要扩大它的活动范围，该怎么处理呢？

生2：只要将绳子放长一点就行。

师生活动：教师用多媒体展示绳子加长后的画面，让学生对比前后两次所形成的圆，比较面积发生的改变。显然，绳子加长后，圆的面积增大了。由此获得结论：圆的面积和圆的半径有直接关联。

设计意图：多媒体是现代教学中重要的辅助工具。教师借助多媒体展示学生感兴趣的羊吃草视频，不但成功揭示了教学主题，而且有效激活了学生的思维，让学生初步感知：圆的半径直接影响圆的面积。圆的半径和面积之间，究竟存在怎样的关系呢？这是本节课要着重探索的问题。这是一个目标明确、条理清晰的导入过程，符合《义务教育数学课程标准（2022年版）》（以下简称新课标）对当前数学教学的要求。

2.活动探索，厘清知识联系

如图1，为了让研究更加直观，教师引导学生借助几何画板进行演示：以正方形的某个顶点为圆心、一条边为半径画圆，并鼓励学生大胆猜想：画出来的圆的面积与正方形面积是什么关系？

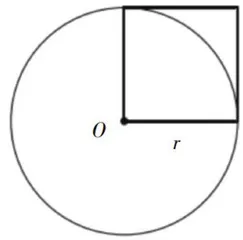
生3：圆的面积应该比正方形面积的4倍少一些。

师：能说说这么想的原因吗？

生4：观察图1，如果将该圆平均分成4份，那么每1份的面积都小于正方形的面积，因此圆的面积必然小于正方形面积的4倍。

师：非常好，如果我们想要明白圆的面积比正方形面积的4倍少多少？该怎么办呢？

生5：可以先分别求出两者的面积，然后运算即可。如图2，若正方形的边长为4，那么圆的半径就是4，正方形的面积为 4×4=16 ，圆的面积只能通过数小格子的方式获得，但圆所对应的小格子存在不满格的情况，只能获得大概数据。

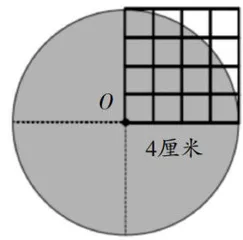
学生在估算的基础上，数出图2中 个圆的面积约为13，那么整个圆的面积约为52。将圆的面积与正方形面积进行对比，计算可得圆的面积约为正方形面积的3.25倍，由此验证了之前的猜想，即圆的面积比正方形面积的4倍少一点。

师：如果换一个圆来研究，这样的关系依然存在吗？请各组按照以上的探索过程，在草稿纸上画图、分析和验证。

学生在自主画图与计算的基础上进行合作交流，展示探索结论

组1：如果正方形的边长为5，那么它的面积就是25，通过数方格的方法可知圆的面积约为78，计算发现圆的面积约为正方形面积的3.12倍。

组2：如果正方形的边长为6，那么它的面积就是36，通过数方格的方式可知圆的面积约为114，计算发现圆的面积约为正方形面积的3.17倍。

...

各组分享交流后，一致认为：在圆的半径与正方形边长相等的背景下，圆的面积为正方形面积的3倍多一点。

师：从以上探索过程中不难发现，圆的面积与正方形面积的关系，实则为圆的面积与其半径平方之间的关系。虽然各组所获得的比值不一样，但它们的区间基本是固定的，这与之前我们所接触过的一个什么知识接近？

生6：圆周率，理由是刚刚所探索的结论都在3.14附近摇摆。

师：据此，可初步形成什么猜想？

生7：圆的面积可能是 π 与半径的平方相乘。

设计意图：新课标强调，课堂上教师要引导学生多尝试，多创造活动，促使学生从中发现规律，形成良好的合情推理能力。在教师恰当的点拨下，学生自主猜想圆的面积公式，取得了较好的成效。

3.操作转化，推导计算公式

师：以上互动，大家初步形成了一个比较有意思的猜想，即圆的面积可能是 π 与半径的平方相乘。这个猜想是否正确呢？可否继续以数方格的方式验证？

生8：数方格的方式验证，误差比较大，应该考虑用其他方式验证。

师：可以用其他什么方式验证呢？

生9：根据以往的学习经验，研究未知图形面积时，可以考虑将它转化为熟悉的图形来研究。

师：哦？圆能转化成什么图形呢？

生10：（犹豫片刻后提出）用“剪拼"法试一试：将圆对半剪开后，无法拼成熟悉的图形；继续将圆剪成4份，拼成的图形见图3，虽然形成的图形有点像平行四边形，但边为曲线，显然不是平行四边形。

师：现在该怎么办呢？

生11：如图4所示，继续剪，将圆平均分成8份，拼接而来的图形比图3更像平行四边形。如果继续剪拼，就会越来越接近平行四边形。

师：不错的想法，现在请大家一起动手操作，验证这种方式行不行。

操作过程：各学习小组取出课前准备好的圆形纸片，平均剪成16份，再拼接；与图3、图4进行比较，说说新的发现。

学生自主操作，教师投影学生的作品（见图5）。

师：观察图5，有什么新的发现？

生12：拼接而来的图形，与原来剪成的8份比，更像平行四边形。将圆平均分的份数越多，所形成的扇形面积就越小，那么圆心角所对每1份的弧线也就越直，如此拼出的图形就更接近平行四边形。

师：将以上几次拼图过程联系在一起思考，会发现圆的平均分的份数越多，拼接而成的图形就越接近平行四边形。咱们一起来看几何画板的演示，如图6所示，如果将一个圆平均分为32份、64份拼接后的图形所发生的变化。

学生表示平均剪的份数越多，拼接而成的图形就越像长方形，由此基本能确定可以将圆转化为长方形。转化而来的长方形，宽为圆的半径，长为半圆的周长，结合长方形面积公式可知，圆的面积为圆周长的 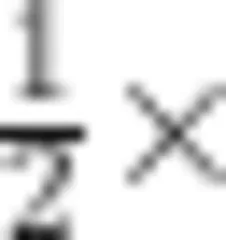半径；若半径用 r 表示，圆的周长为 2π r ，由此可知拼接而成的长方形面积就是 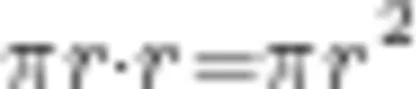，圆的面积公式由此形成。

师：观察所获得的圆面积公式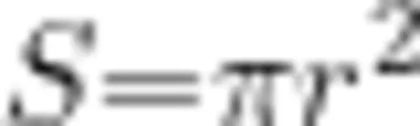 ，可见圆的面积与半径的平方存在怎样的联系？

生13：结合以上探索，可知圆的面积为本身半径平方的 π 倍，这说明之前的猜想是正确的。

设计意图：教师借助操作活动，唤醒学生已有的学习经验，引导学生应用数学转化思想，将待研究的圆的面积问题转化成熟悉的长方形面积。虽然学生已经具备了初步的转化思想，但是圆本身属于曲线，想要化曲为直，对于学生而言确实有一定的难度。为此，教师在学生的思维生长处及时进行点拨、启发，并鼓励学生在独立思考的基础上探索与交流，能够有效提高学习效率。

在此过程中，教师没有为学生提供自主探索的机会，而是让学生直接拼接平均分成16份的圆，这样学生虽然能感知将圆转化成长方形的过程，但是整个过程的思维跨度过大，学生难以从真正意义上理解“为什么要这么拼接”。由此可见，教师要充分尊重学生的认知发展规律，顺应学生的思维进行教学，虽然在教学进程上看似“慢一些”，但是能让学生从真正意义上达到深刻理解的目的。

二、几点思考

1.如何贯彻"以生为本"的理念

新课标强调学生在课堂中的主体地位，教师组织的教学活动都应基于“以生为本"的理念来实施。鉴于学生才是课堂真正的主人，教师在设计教学时要将学生的自主探索、合作交流等放在首位，将发展学生的思维能力作为教学的重要目标。

“以生为本"的理念是指教师要尊重学生的主体地位，尊重学生的个性差异，把充分发挥学生的主体作用作为教学的出发点和归宿。

小学数学教学要体现“以生为本"的理念，教师要做到“五个坚持”：一是坚持把发现的机会让给学生，激活学生的问题意识，改变学生的学习方式，变关注学生回答问题为关注学生发现问题；二是坚持把思考的时间留给学生，引导学生在数学学习过程中做到思考、思考、再思考，让学生有充足的自主学习时间，使学生的思考能力不断提高；三是坚持把动手的过程放给学生，学生的事尽量让学生做；四是坚持把学习的空间还给学生，学生有了充裕的自主学习空间，就能把自己想说的说出来，把自己想写的写出来，把自己想做的做出来；五是坚持把评价的权利交给学生，让学生自我评价，让学生互相评价，这样才能不断改进教学的方式方法，使数学教学按照一定的方向有序进行。