几何直观素养下思维可视化教学

几何直观指借助直观的图形分析与描述问题的过程。几何直观可将原本复杂的数学问题变得简洁、形象化，让学生在“数形结合"思想的辅助下，准确探索解决问题的路径，提高数学理解能力[1]。同时，直观的数学表现形式可促使学生思维的可视化，即将一些看不见、摸不着的内隐思维以图的形式直观表达。尺规作图是让学生思维可视化的重要路径，也是培育学生几何直观素养的关键举措。

一、教学过程设计

1.情境创设，认识尺规

课堂导人环节，教师借助多媒体展示一段芭蕾舞表演的视频，在学生观赏后提出一些问题与他们共同探讨。

师：大家对芭蕾舞表演最深的印象是什么？

生1：演员们旋转的动作太美了。

师：我也是这么认为的，表演者旋转时形成了什么数学图形？

生（齐声答）：圆。

师：不错，这一现象在生活中有没有遇到过？

生2：有，比如冬天在雪地里，保持一只脚在原地，另外一只脚伸直在雪地里转一圈，那么在雪地里就形成一个圆形。

师：真是个有趣的玩法，现在请大家看我手中拿的是什么（展示圆规）？根据芭蕾舞者与我们在雪地画圆的方法，能不能想到这是干什么用的？

生3：圆规，就是用来画圆的。它的两条腿与我们的两条腿一样，保持一条腿不动的情况下，旋转另一条腿，则会获得一个完整的圆。

设计意图：学生能接触到的数学知识都源于生活实际，为了让学生更好地理解教学内容，最好的办法就是将知识还原到生活实际中去，让学生基于直观的视角观察与分析教学内容，这是促进生活与数学联系的重要途径。考虑到学生有一定的生活经验基础，因此借助芭蕾舞视频引发学生对圆的认识，让学生主动联想到雪地画圆的经验，能为顺利引出圆规这一数学工具奠定基础。学生在直观视频刺激下，不仅自主抽象出圆，还提升了数学审美能力，增强了对知识的探索欲。

2.自主研究，理解尺规

师：圆规是一种重要的数学绘画工具，现在请大家在草稿纸上用圆规画出自己想要的图形，并将自己在画图过程中遇到的困难表达出来。

生4：我本想画一个完整的圆，奈何画图过程中，装铅笔的那一只脚不听使唤，总是乱动，导致画出一段没有规律的曲线。

生5：画图时，那个针尖总是乱跑，虽然画了一个圆，但不太圆（尴尬地笑）。

师：以上两个同学遇到的问题，相信不少同学都遇到了，那么该怎样解决这些问题呢？

生6：画图过程中，应将针尖紧紧按在纸上，不让它乱跑，同时要保持笔尖的位置不上下移动，这样旋转时画出来的圆才圆。

生7：还要注意画圆时的力度，因为用力不均匀的情况下，圆规的脚是会乱动的。

生8：画圆时，必须紧握圆规顶端的位置，切忌将手握在圆规两只脚上。

师：你们说得都有道理，现在请大家来看老师的标准示范。用手握在圆规的顶端，不触碰圆规的两只脚；保持针尖位置恒定不动；确保圆规两只脚之间的距离一致，用恰当的力度缓慢旋转一周。有没有哪位同学知道，为什么只有在保持圆规两脚之间的距离不变的情况下，才能画出圆？

生9：如图1，圆规两只脚之间的距离恒等不变时，所画出来的圆才圆。

师：确保圆规针尖到圆弧上的每一点距离均一样，这一特点能帮助人们解决很多生活实际问题呢！

设计意图：学生是学习的主人，数学学习是学生独立思考、自主探究、实践操作、合作交流等模式的组合。圆是学生日常生活中遇到过的图形，学生对此并不陌生，因此鼓励学生自主探索圆规画圆的方法，不仅体现了学生学习的主动性，还促使学生在主动探索的基础上掌握圆规的使用方法，此为提升学生自主探索与合作学习能力的基础。针对圆规画圆容易出现的一些问题，师生共同探索，提炼出完整的应用技巧，使得学生对“圆规针尖到圆弧上任意点的距离恒等"产生明确认识，为接下来的教学做好铺垫。

3.问题探索，完善认知

师：如图2，树桩上拴着一条狗，附近地上散落着一些骨头，你们觉得小狗能吃到几号骨头？

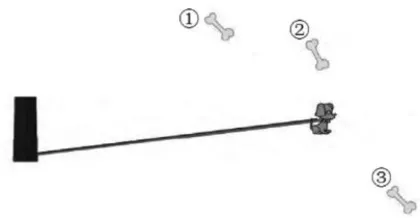
生10：从直观的图来看，小狗可以顺利吃到 ① 号骨头，原因在于 ① 号骨头处于小狗的最远活动范围之内；小狗肯定吃不上 ③ 号骨头，因为这根骨头并不在小狗活动的范围之内；关于 ② 号骨头小狗是否能吃到，用肉眼难以辨别。

生11：目测 ② 号骨头到树桩的距离大于绳长，因此这根骨头不在小狗能接触到的范围内。

生12：我认为 ② 号骨头到树桩的距离小于绳长，因此小狗可以接触到这根骨头，应将这根骨头判定为小狗能吃到的范畴。

师：从反馈情况来看，大家对 ① 号与 ③ 号骨头不存在异议， ② 号骨头究竟在不在小狗的活动范围内呢？想要确定这个问题，关键在于什么？

生13：只要比较“骨头与树桩之间的距离"与“小狗与树桩的距离”，如果前者长，就表示小狗无法吃到骨头；如果后者长，则表示骨头处于小狗的活动范围内，小狗可以顺利吃到骨头。

师：描述得很清楚，为了便于理解，现在我们一起将树桩、小狗以及各根骨头用点表示，分别连接树桩所表示的点与各根骨头和小狗所表示的点，形成多条线段（见图3）。如何比较这些线段的长短，获得问题的结论呢？请大家先独立思考，再以合作学习的模式借助圆规与没有刻度的直尺进行测量，组内讨论测量结论。

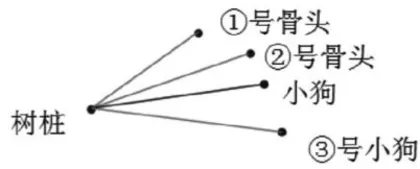
生14：首先用不带刻度的直尺测量小狗与树桩之间的距离，并在直尺相应的位置做好标记，然后对着这个标记，分别测量其他三条线段的长度。测量发现， ① 号 ② 号骨头与树桩的距离小于或等于小狗与树桩的距离，因此小狗可以吃到这两根骨头，但 ③ 号骨头与树桩之间形成的线段要大于小狗与树桩之间的距离，因此小狗吃不到 ③ 号骨头。

生15：将圆规的针尖对准树桩的点，另一只脚对准小狗所在的点，保持圆规所张角度不变，分别与其他三根线段比长短，可以发现小狗可以吃到① 号 ② 号骨头，吃不到 ③ 号骨头。

生16：用圆规判断更简便，首先将圆规的针尖对准树桩的点，以小狗所处的位置作为圆规上铅笔的起点画弧线，观察各根骨头是处于弧线内还是弧线外。通过圆规作图发现： ① 号骨头处于弧线内， ② 号骨头处于弧线上，因此小狗可以顺利吃到它们；③ 号骨头处于弧线外，小狗吃不到。

师：以上三种方法都很好，如果将这三种方法用简略图表示，该怎么画呢？

生17：如图4，分别将以上三种方法转化为直观的图。

学生再次揣摩这三种方法，经过讨论，一致认为第一种方法容易出现偏差，后面两种方法类似，都能准确描述哪几根骨头处于小狗活动范围之内，由此揭示树桩与圆弧上的每一点的长度都相等。

设计意图：关于小狗能吃到哪根骨头的问题成功激起了学生的探索兴趣。将与生活息息相关的问题抽象成简单的数学图形，体现了几何直观对解决问题的重要作用，同时也凸显了学生思维可视化的过程。教师引导学生对问题的探索，为学生用尺规作图绘制已知线段的等长线段奠定了基础。

4.实践操作，实际应用

如图5，此为一条线段 ，请用 直尺与圆规画一条线段 C D 使 □

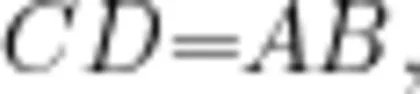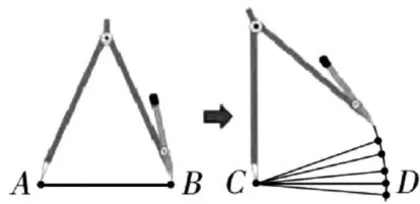
画法1：如图6，先画一条射线CE，将圆规两脚对准线段 A B 到 C E 上截取 C D=A B 即可。

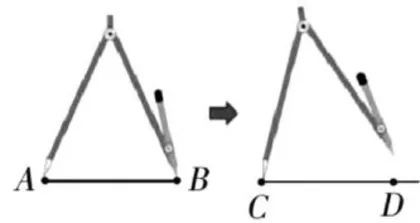
画法2：如图7，用圆规两脚确定 的距离，再任取一点作为点 ；以点 C 为固定点，圆规两脚距离保持不变的情况下画圆弧，那么点 C 到圆弧上的任意一点的长度均与 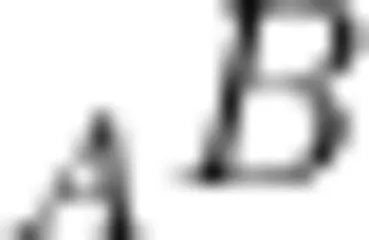的长度相等。

教师肯定了学生所提出的两种画法，并要求学生思考：为什么画出来的线段 与线段 的长度是一样的？学生分别从不同的维度回答教师所提出的问题，凸显了思维可视化的过程，为发展几何直观素养奠定了基础。教师在此基础上，用多媒体展示一些没有刻度的直尺与圆规合作后形成的美丽图案，并要求学生对照相应的图案尝试自主画一画，以提高数学学习的趣味性。

设计意图：学生用尺规自主画出已知线段的等长线段，看似简单，但存在不少问题。教师鼓励学生自主尝试、思考与分析，让学生在合作交流过程中表达自己的想法，在思维可视化的基础上提高几何直观能力。如此设计，不仅体现了新课标背景下的“生本"理念，还突出了数学“深度学习"理念，彰显了数学尺规作图的价值所在，对培养学生的空间观念与推理意识都有一定的作用。不同画法的比较，进一步启迪了学生的思维，让学生充分体会了数学操作的重要性与必要性。

二、教学思考

1.“做中学"是学生思维可视化的基础

“做中学"理念强调学习者可通过实践活动来获得相应的学习内容，亲历知识形成的过程，远远超越间接获取结论的效果[2]。纵观本节课的教学，教师一共为学生提供了三个“做中学"的机会：第一次，鼓励学生自主研究如何使用圆规，让学生在实践中总结出使用规则与注意事项；第二次，关于小狗吃骨头的情境探索，核心在于比较线段的长短，让学生通过实践优化了思维，体现了几何直观的重要价值；第三次，画已知线段的等长线段，学生在主动探索与合作交流的基础上进一步夯实了知识基础，体会了数学学习的科学、严谨的精神

2.几何直观可拔高学生的数学思维

几何直观能让学生更好地理解数学知识，为提炼思想方法奠定基础。本节课，教师应用芭蕾舞、小狗吃骨头等丰富有趣的生活情境，成功激活了学生的思维，增强了学生的课堂探索欲。然而，这并不是教学的真正目的所在，核心素养背景下的数学教学必然以学生的发展为主。在教师的引导下，学生学会用数学的眼光观察芭蕾舞和小狗啃骨头问题，将生活现实抽象成简洁明了的数学直观图形，不仅提升了几何直观能力，还真正发展了思维。学生的表征过程就是揭示思维的过程，可视化的思维进一步催生了学生的问题意识，让课堂充满探索味。

3.深入探索是发展创新能力的根本

尺规作图离不开学生的动手动脑过程，手脑协作可有效提升学生的几何直观能力。新课改背景下，数学教学关注的是深度学习，这就离不开学生深度探索的支持，而深度探索是发展其创新意识的关键措施。本节课在尺规的辅助下，学生勇敢地尝试、思考与探索，学会了从不同的视角观察与分析问题，切实体会了作图对发展几何直观能力的重要价值。

总之，数学是一门艺术，“尺规”是表达这门艺术的基本方法。尺规作图教学不仅能有效提升学生的几何直观能力，还能凸显思维的可视化，让课堂充满生机与活力，此为发展学生核心素养的重要路径。

参考文献：

[1］李芳芳.做中学：培育几何直观和推理意识：“作等长线段"教学片断与思考[J].小学数学教育，2024（12）：39-41.

[2]叶艺灵．小学数学教学中几何直观能力的培养策略[J].数学学习与研究，2018（2）：66.