聚焦整体建构 发展学生素养

在"双减"政策背景下，数学学科教学应聚焦于学生的学科能力及核心素养的全面培养。在课堂教学中，教师应着重引导学生学会用数学的眼光观察现实世界，学会用数学的思维剖析现实世界，学会用数学的语言描述现实世界[1]。传统的课时教学容易破坏知识间的内在联系，影响个体知识体系的建构，影响学生数学核心素养的发展。因此，在小学数学教学中，教师应从整体视角进行规划，让学生将相关的知识内容串联起来，提高学生知识迁移能力，培育学生数学核心素养。笔者以“多边形的面积"教学为例，谈谈如何通过整体规划，发展和提升学生数学核心素养。

一、聚焦整体设计，探寻核心素养培养路径

1.分析教材，明晰核心素养发展现状

数学是一门逻辑性较强的学科，数学知识之间有着千丝万缕的联系。教材是以知识的逻辑顺序、学生的认知顺序、学生的心理发展顺序的“三序结合"原则编写的。对于一些相同或相关的知识内容，因受学生的认知能力、学生的心理发展顺序等因素的影响，这些知识内容可能分散在不同的章节中。在实际教学中，教师要打破章节束缚，从整体建构的角度发展学生的数学核心素养。

比如，“多边形的面积"这一章内容涉及平行四边形、三角形、梯形及组合图形的面积计算公式和应用。从人教版教材编排上来看，三年级上册学习长方形和正方形的初步认识；三年级下册学习面积与面积单位，掌握长方形和正方形的面积计算公式；四年级上册学习面积单位换算，掌握平行四边形、梯形的概念和基本特征；四年级下册学习三角形的概念及性质，这些知识为学生学习本单元内容创造了条件。本章内容后，学生在五年级下册学习长方体和正方体的表面积、体积；六年级上册学习圆的周长和面积；六年级下册学习圆柱和圆锥等相关内容。教学内容的安排遵循了学生的认知规律，即由直观到抽象、由简单到复杂。教师要清晰把握知识发展脉络，从而使课堂教学设计自然、流畅。

在学习“多边形的面积"前，学生已经学习了面积、面积单位及面积单位换算等相关内容，其数据分析和数学运算素养已得到一定的发展。后续学生将学习圆、长方体、正方体、圆柱与圆锥等知识，从而进一步发展自身的模型意识、推理意识等核心素养。

2.整体规划，明确核心素养生成路径

在"多边形的面积"教学中，教师要直面学情，引导学生提炼单元研究线索，即将未知转化为已知。比如，教学平行四边形时，教师可以引导学生通过剪拼将其转化为长方形来研究；教学三角形面积时，教师可以引导学生将三角形通过剪拼转化为平行四边形来研究。笔者明确单元研究路径后，确定了“多边形的面积"单元教学流程：（1）在探索平行四边形面积时，教师要引导学生通过割补、拉伸等实验活动将其与长方形建立联系，得到平行四边形面积计算公式，发展学生直观想象、数学建模等素养；（2）在探索三角形和梯形的面积时，启发学生将它们与平行四边形建立联系，由此借助平行四边形面积公式推理得到三角形和梯形面积公式，发展学生模型意识、几何直观、推理意识等核心素养；（3）在探究组合图形的面积时，引导学生结合以上探究经验将不规则、陌生的图形转化为规则、熟悉的图形，进一步发展学生几何直观、空间观念、推理意识等核心素养。

以上知识内容呈现由浅入深、由简人繁的特点，符合学生的认知发展规律，能够有效调动学生参与课堂的积极性，让学生在主动参与中逐步培养数学核心素养。

二、聚焦教学实践，在操作中发展学生核心素养

数学核心素养的培养是一个慢过程。在日常教学中，教师应创造机会让学生主动参与课堂教学实践，引导学生经历观察、思考、交流、归纳等学习过程，培养数学核心素养。

比如，在“多边形的面积"教学中，教师通过设计实践活动让学生动手做、动脑想、动口说，通过具身体验发展其数学核心素养。

1.设计观察活动，发展数学核心素养

直观观察可以让学生对所学知识获得充足的感性体验，不仅易于学生理解和掌握，而且可以让学生对所学知识形成充足的体验，获得深刻的认识。因此，在几何与图形相关内容的教学中，教师可以设计一些观察活动，让学生更好地感知数学知识，形成相应能力，发展其几何直观素养。

比如，在教学“多边形的面积”时，笔者结合学生已有知识经验设计了“图形的转化"观察活动。

活动1：如图1所示，将左侧长方形斜着剪一刀，剪下一个三角形，将这个三角形平移放在原长方形的另一侧。结合这一操作过程，思考如下问题： ① 剪拼后，原来的长方形变成了什么图形？ ② 剪拼前后，周长和面积发生了怎样的变化？ ③ 如果将右侧的平行四边形转化为长方形，可以如何操作？

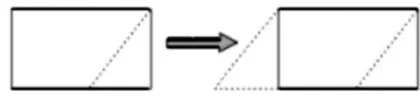
学生通过直观观察很容易得到答案：将剪下的三角形通过平移拼接后，长方形变成了平行四边形，虽然图形的形状变了、周长变了，但是图形的面积不变。借助这一不变的本质，能为学生推导平行四边形的面积公式创造条件。

活动2：如图2所示，将左侧两个完全一样的直角三角形拼接在一起，可以得到怎样的图形？拼接后，三角形的面积与拼接后的图形具有怎样的数量关系？如果将两个完全一样的普通三角形拼接在一起，能够拼成什么图形？拼接前后面积如何变化？

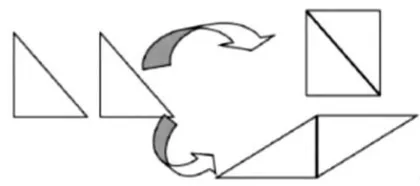
学生通过直观观察可知，将两个完全一样的直角三角形拼接在一起，既可以拼成一个长方形，也可以拼成一个平行四边形。不管是拼成长方形还是拼成平行四边形，三角形的面积都是它们的一半。在此基础上，笔者通过创设问题引导学生将问题一般化“两个完全一样的普通三角形可以拼成怎样的图形”，使普通三角形和平行四边形建立联系。

在推导梯形的面积公式时，学生可以采用同样的研究路径，思考两个完全一样的直角梯形可以拼成什么图形，由此将梯形与长方形和平行四边形建立联系，从而利用长方形或平行四边形的面积计算公式，推导梯形的面积计算公式。通过“图形的转化”既能发展学生的几何直观、空间观念素养，又能提升学生的推理意识。

2.设计测算活动，发展数学核心素养

在"多边形的面积"教学中，教师可以组织学生开展多边形的测量与计算，这样既可以培养学生的动手能力，又能培养学生用定量的方法分析问题、解决问题的学习习惯，让学生体会数学的应用价值，发展其数据分析素养。教师引导学生通过测量、计算、交流，能让学生发现蕴含其中的道理，抽象数学模型，发展数学素养。

比如，在教学“平行四边形的面积"时，教师安排了测量和计算活动。

（1）测量

教师为每个学生准备一张大小形状完全相同的平行四边形卡纸，让学生分别测量平行四边形的底边长、斜边长和高。

学生独立测量，教师展示学生的测量结果：有的学生以厘米为单位，有的学生以毫米为单位，得到两组数据： ① 底边长 ，斜边长6cm，高4cm；

② 底边长 80mm， 斜边长 60mm 高 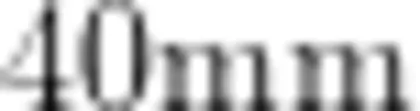教师呈现学生的测量结果并引导学生分析数据，让学生利用统一度量单位度量物体，从而为计算扫清障碍。

（2）计算

测量后，教师让学生根据测量数据计算平行四边形的面积。学生独立思考，教师巡视，并投影展示具有代表性的算式 。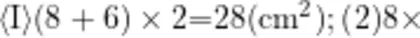

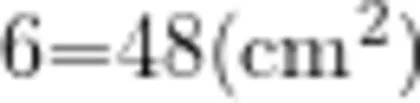
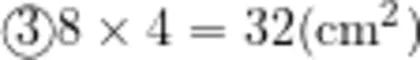（3）交流

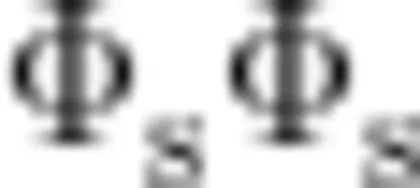对于以上计算结果，教师让学生先分组讨论，然后呈现分析过程。对于以上结果，学生给出解释：对于算式 ① ，将平行四边形的底边长和斜边长相加乘以2，显然所求的结果是平行四边形的周长，而非平行四边形的面积，所以是错误的。对于算式 ② ，将平行四边形的邻边相乘，该方法是大多数学生的选择。然而平行四边形具有不稳定性，如果将平行四边形不断拉伸，显然长方形的面积是变化的，因此利用邻边相乘的方法是行不通的。对于算式 ③ ，用底边与高相乘，同样可以根据平行四边形不稳定这一性质来解释。随着形状的变化，平行四边形的高也随之发生变化，平行四边形通过拉伸可以将其变成长为 、高为6cm的长方形，由此可以推断出平行四边形的面积计算公式，即S平行四边形=底 高。

由此，通过分析测算结果，学生逐渐抽象出平行四边形面积的计算公式，培养了数据分析、推理意识和模型意识等核心素养。

3.设计迁移练习，发展数学核心素养

在学生学习本章基础知识、掌握基本方法后，教师有必要设计一些综合性练习，让学生加深对相关知识方法的理解，提高其分析和解决问题的能力，增强其解题信心，进一步发展其模型意识、推理意识等核心素养。

练习1：如图3所示，计算不规则图形的面积。

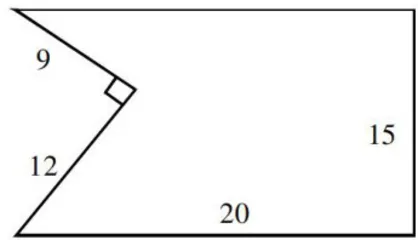
解析：练习1难度不大，但综合性较强，既考查学生对三角形面积和长方形面积的掌握情况，又考查学生图形转化意识及转化能力。对于该题，学生可以通过“填补"将不规则图形转化为长方形，利用长方形面积减去直角三角形面积得到不规则图形面积。

练习2：如图4所示，王大伯用51米的栅栏靠墙围了一块梯形菜地，求菜地的面积。

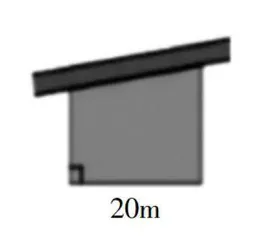
解析：练习2是一道实际应用题，难度较小，主要考查学生对梯形面积公式的掌握情况和数据分析能力，旨在提高学生的数学应用意识。

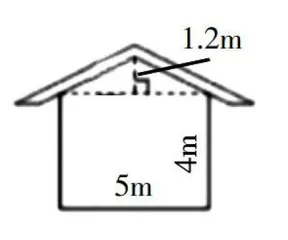
练习3：图5是某公园一面墙，如果每平方米需要185块砖，请问砌这面墙大约需要多少块砖？

解析：该题实际考查组合图形的面积。学生在灵活运用所学解决实际问题的过程中，既开阔了视野，又提高了分析和解决问题的能力。

问题给出后，教师可以预留一定的时间让做错的学生说说他们的解题过程，并通过师生、生生互动交流寻找错因。学生在析错、纠错的过程中能加深对相关知识的理解，提高发现、分析和解决问题的能力，培养数学核心素养。

三、结语

数学核心素养的培养是一个长期的过程，它不是只依靠教师讲授达成的，而是学生在日常学习中逐渐形成的。在日常教学中，教师应从学生的认知特点出发，合理设计教学方案，为学生创造适合他们开展各种探究活动的条件，使他们在活动中发散思维，发展个性，提高运用知识解决实际问题的能力；同时，通过各种活动加深学生对数学知识的理解，让学生感受数学学习乐趣，培养其数学应用意识。比如，在“多边形的面积"教学中，教师应从整体视角分析，进行整体教学设计，通过开展有效的探究活动激发学生的数学学习兴趣，让学生在积极参与中逐步提高自身的数学能力与核心素养。

总之，在教学中，教师应认真了解学情，分析教学内容，从整体视角出发，合理创设数学活动，引导学生将分散的知识串联起来，建构完善的知识体系，逐步发展其数学核心素养。

参考文献：

[1]胡连成.“情境—问题—思维"视角下的数学情境设计解析[J].教学月刊·中学版（教学参考），2022（12）：21-26.