亲历实践过程，形成“三会”素养

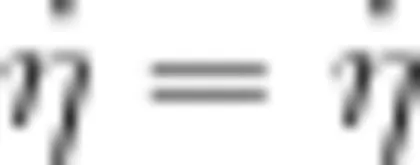
综合与实践活动能帮助学生联系数学知识和生活情境、数学学科和其他学科，让学生运用数学知识解决生活中的实际问题，解释生活中的具体现象，从而让学生会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。

综合与实践活动“自行车里的数学”，主要是让学生在活动中学会学习和理解数学知识，感悟知识存在的价值。

一、课前思考

“自行车里的数学”是学生学习“比例”单元后的综合与实践活动，目的是让学生运用学过的圆、排列组合、比例等知识观察生活中的自行车，感受数学在生活中的广泛应用。教师要引导学生经历“发现问题一提出问题—分析问题一建立模型—寻找答案一解释应用"的问题解决过程。

“自行车里的数学”一课要研究两个问题：一是研究普通自行车的速度与自行车内在结构的关系，让学生找一辆普通自行车测量其前齿轮齿数、后齿轮齿数和车轮半径，探究前齿轮、后齿轮的齿数与它们转数的关系，计算自行车转1圈的路程；二是研究变速自行车能变化出多少种速度，让学生找一辆变速自行车测量其前齿轮、后齿轮的齿数，思考转同样的圈数哪种组合使自行车走得最远。

因此，笔者将本节综合与实践活动的教学目标确定为：（1）让学生经历“自行车里的数学"的探究过程，发现“普通自行车的速度与自行车内在结构的关系"和“变速自行车能变化出多少种速度”；（2）获得“四能”，形成“三会"素养，体会数学与生活的紧密联系。

二、教学活动

1.认识自行车的组成，感悟"一-对应"思想

师：同学们，你们想过简单的自行车里藏着我们学过的哪些数学知识吗？

学生回答：（1）自行车上面有三角形的架子，运用了三角形具有稳定性的特征；（2）自行车的车轮在旋转，是图形的运动；（3）自行车的两个轮胎是圆形的，用到了圆形的知识。

师：这节课我们就来研究“自行车里的数学”。你们知道自行车是如何行进的吗？

生1：自行车踏板带动前齿轮，前齿轮带动链条，链条带动后齿轮，后齿轮带动后轮，后轮带动整个车身，车身带动前轮，于是自行车就往前动起来了。（学生鼓掌）

师：我们知道自行车靠后轮往前推，前轮用于控制方向。当前齿轮、后齿轮、链条、后轮、前轮这些零件组合在一起，就变成了自行车里最重要的部分，这便是自行车的动力系统。大家看，当踏板转1圈时，前齿轮刚好转动了1圈。前齿轮上面有一个个尖尖的凸起，我们把它叫作小齿。一个尖尖的凸起叫作1齿，同学们数一数前齿轮和后齿轮分别有多少齿？

生2：前齿轮的齿数是14，后齿

轮的齿数是 10

师：我们来观察，链条中间有一个个小洞，把齿轮装在链条上面，1个小齿刚好对应1个洞。你们能联想到数学上的哪个词？

生（齐声答）：一一对应的数学思想。

在这个教学片段中，教师采用聊天的方式引导学生思考自行车里藏着的数学问题，拉近数学知识与生活实际的关系，促使学生体会自行车的组成里有很多数学应用。随着师生之间聊天的层层推进，学生知道了前齿轮、后齿轮和链条等名词，知道了前齿数和后齿数，还从前齿轮1个小齿对应链条上的1个洞，感悟一一对应的数学思想。

2.研究走多远的原因，感悟“变与不变”思想

师：自行车是交通工具。说到交通工具，你们觉得这辆自行车能走多远，哪些因素会影响它走多远？

生3：我觉得是车轮的大小和齿槽的多少。一辆自行车如果车轮大一些，肯定会走得远一些；车轮小一些，就会走得近一些。

生4：我觉得是车轮的周长，车轮的大小和车轮转动的速度都会影响自行车是走得远，还是走得近。

师：有同学说车轮的周长会影响自行车走多远，对此你们联想到了什么？

生5：车轮旋转的圈数，自行车转1圈和转10圈的路程肯定不一样。

师：车轮转动的速度由什么决定呢？比如小孩子骑自行车和大人骑自行车，他们的速度肯定不一样，看来骑车人的能力影响了自行车的速度。刚才我们说很多因素会影响自行车走多远，数学要研究的是这些千变万化之中不变的东西。你们想一想：如果让同一个人骑同一辆自行车，自行车能走多远由什么因素来决定？

生6：这取决于他转几圈自行车。

师：那我们从简单的转1圈开始，研究这辆自行车能走多远，好吗？

在这个教学片段中，教师借助“哪些因素会影响自行车走多远"这个大问题，让学生先漫无边际地寻找原因，再从数学角度寻找原因，寻找在变化中不变的东西，从而发现自行车能走多远的根本原因是骑行者转几圈自行车，在这个思考过程中帮助学生感悟"变与不变"的思想方法。然后，教师引导学生从最简单的自行车转1圈开始研究，体会数学中“化繁为简"的数学思想方法，这有利于学生探寻问题的答案。

3.探索走多远的方法，感悟“转化"思想

师：同学们，想要解决“自行车能走多远"这个问题有什么好办法？

生7：我觉得可以用转的圈数来乘自行车车轮的周长。

师：意思是用数学上的“算”，你们觉得最直接的方法是什么？

生8：就是一个人坐在自行车上，另一个人用卷尺量出自行车车轮转1圈的距离。

师：如果要测量自行车车轮转1圈的距离，我们该怎么办？

生9：我们可以先固定一个点，然后骑着自行车转1圈，在结束的地方画一个点，最后用卷尺量出这两个点之间的距离，就是自行车车轮转1圈走的路程。

师：这个方法很简单，它有没有什么不好的地方？

生10：量的时候可能遇到尺子不够长，会导致我们测量不准确；如果骑车的那个人转1圈的时候不是走的直线，这样我们量出来的长度就不准确了。

师：量出自行车车轮转1圈的距离可能会有误差，于是我们想到了更有数学味的“算”。刚才有同学说计算自行车车轮转1圈走的路程可以用转动的圈数乘周长，自行车车轮的形状是圆形的，算自行车车轮的周长就是算圆的周长。接下来我们重点研究后轮转动的圈数。想一想，后轮转动的圈数就是谁转动的圈数？

生11：后轮转动的圈数和后齿轮转动的圈数有关。

在这个教学片段中，为了解决“转1圈自行车能走多远”这个实际问题，教师引导学生联系"量"和"算”这两种方法。学生通过分析发现"量”虽然直接，但是会有误差。于是，学生放弃了“量”，采用具有数学味的“算”。学生在猜想中尝试将“转1圈自行车能走多远"转化为计算转动的圈数乘周长，由于自行车车轮的周长是固定的，因此将这个问题转化为研究转动的圈数问题，在不断思考中逼近问题的本质。

4.解决走多远的路程，感悟“推理”思想

师：以四人为一小组，合作研究自行车转1圈时，前齿轮和后齿轮之间有怎样的关系？

生12：我们组测出来是前齿轮转1齿，后齿轮也转1齿然后我们把前齿轮转1圈，发现前齿轮和后齿轮都转了14齿。我不明白为什么前齿轮和后齿轮的齿轮数不一样，但是它们转1圈的齿数是一样的？

生13：我觉得虽然前齿轮齿数多于后齿轮齿数，但是前齿轮是带动后齿轮在转，所以前齿轮的齿数和后齿轮的齿数是一样的。

师：听清楚了吗？前齿轮转1齿的时候，后齿轮也转1齿。（实物演示操作）前齿轮转1圈，也就是前齿轮转过14齿，后齿轮也要转过14齿。但是后齿轮只有10齿，后齿轮要转14齿，说明后齿轮转的圈数要比前齿轮多。现在你明白了吗？我们发现前后齿转动的总齿数虽然是相等的，但是它们转动的圈数是不一样的。

生14：我们发现了前齿轮转动的 总齿数等于后齿轮转动的总齿数，因 为前齿轮转动的总齿数等于前齿轮 齿数乘前齿轮转动的圈数，后齿轮转 动的总齿数等于后齿轮齿数乘后齿 轮转动的圈数，所以前齿轮齿数乘前 齿轮转动的圈数等于后齿轮齿数乘 后齿轮转动的圈数。（学生鼓掌）

师：谢谢你，太了不起了！现在我们要研究的是当前齿轮圈数为1的时候，求后齿轮的圈数。

生15：前齿轮转1圈，后齿轮就要转1.4圈。因为“前齿轮齿数 × 前齿轮转动的圈数 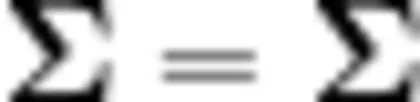后齿轮齿数 × 后齿轮转动的圈数”，我们已经知道了三个量，就能算出剩下的量了。

师：当前齿轮转1圈时，后齿轮转动的圈数等于前齿轮齿数除以后齿轮齿数，后齿轮转动的圈数就是车轮转动的圈数。我们只要再知道车轮的周长，利用“车轮转动的圈数 × 车轮的周长"就能算出车轮转1圈自行车能走多远了。

在这个教学片段中，教师放手让学生通过小组合作讨论，发现前后齿轮圈数的关系。在教师的层层分析和步步推理中，学生通过动手操作将“自行车转1圈能走多远"转化为“前齿转动的总齿数 σ=σ 后齿转动的总齿数”，再通过数量关系“齿轮转动的总齿数 ？= 齿轮的齿数 × 齿轮转动的圈数”转化为“前齿轮齿数 ？× 前齿轮转动的圈数 τ=τ 后齿轮齿数 × 后齿轮转动的圈数”，最后观察到前齿轮齿数是14、后齿轮齿数是 10 当前齿轮圈数为1时，学生推理得到"后齿轮圈数 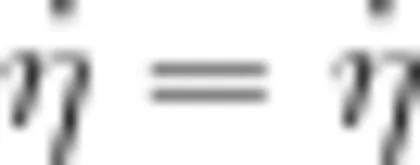前齿轮齿数 ÷ 后齿轮齿数”。只要知道后轮周长，就能计算出转1圈自行车行进的路程。这个学习过程给学生独立解决问题做了很好的示范，引导学生先将未知问题逐步转化成已知问题，再进行严谨细致的推理，最终解决未知的问题。

三、教学反思

1.用数学的眼光观察现实世界

在活动中，教师引导学生用数学的眼光去观察自行车的构造，特别是前后齿轮的比例关系以及它们与车轮转动的联系。这一环节的设计，旨在培养学生从日常生活中发现问题和抽象出数学问题的能力。笔者注意到部分学生在观察时缺乏系统性，容易忽略细节。因此，教师要引导学生进行系统的观察，从多个角度捕捉问题中的数学元素。

2.用数学的思维思考现实世界

在深入阶段，教师鼓励学生运用数学的思维去分析自行车行驶过程中涉及的数学问题。这一过程中，学生展现出较强的逻辑思维能力，能够运用比例、代数等数学知识解决实际问题。笔者发现，部分学生在面对复杂问题时，容易陷入思维定式，难以跳出常规框架去寻找新的解决途径。因此，教师要培养学生的创新思维和批判性思维，引导他们学会从不同角度审视问题，运用多种方法解决问题。

3.用数学的语言表达现实世界

在交流环节，教师要求学生用数学的语言来表达他们的观察结果、分析过程和解决方案。通过实践，大部分学生能呈现自己的研究成果，但在口头表达方面还存在不足。因此，教师要加强学生的数学口语训练，提高他们的数学表达能力；同时，要鼓励学生多参与小组讨论和课堂展示等活动，以增强他们的自信心。

总之，《义务教育数学课程标准（2022年版）》中关于“应用意识”明确提出：“应用意识有助于用学过的知识和方法解决简单的实际问题，养成理论联系实际的习惯，发展实践能力。"综合与实践活动"自行车里的数学"表面上看似教师在教学自行车里藏着的数学知识，其实是在利用学生的已有知识经验解决生活中的实际问题，让学生在探究活动中感悟数学思想方法，培养其应用意识和创新精神，提高其解决问题的能力，发展其核心素养。