有效凸显：将学习引向深处

随着新课程改革的深化，关注课堂教学的有效性已成为当前教育教学的热门话题。教师要深入解读教材，分析教学内容，了解具体学情，有效凸显教学要点，将学生的数学学习引向深处，使学生对数学理解逐步走向深刻。这里所说的“有效凸显"可以从宏观与微观两个层面来理解：从宏观层面来看，有效凸显是指要凸显教学要点，任何一个教师在实施教学的过程中都应思考这门学科的教学到底能够给学生带来什么，这是教学过程中教师必须思考和回答的问题，也是教学要点得以凸显的关键；从微观层面来看，在具体学科知识教学的过程中哪些教学要点能够被凸显、如何被凸显，学生如何在学习知识的过程中形成思维的生长点，如何在运用知识的过程中认识到重点和要点，这些同样是“有效凸显"必须关注的课题。教师要基于宏观与微观层面的理解，在教学中做出相应的努力，将学生的学习有效引向深处。

对于小学数学学科而言，教师既要认识到这门基础学科的重要性，也要关注学生在数学学习过程中的体验，要思考如何通过有效凸显来优化学生的学习过程、提升学生的数学学习品质，从而顺利发展学生的数学核心素养。笔者在“乘法分配律”一课的教学中，通过有效凸显教学要点，将学生的数学学习引向深处。

一、简析教学过程

1.生活引入，感知规律

导入：你最喜欢爸爸还是妈妈？在课前，老师做了一个小调查，我们班好多同学的爸爸妈妈每天都会很早起床准备早点、接送我们上下学、辅导我们的功课。爸爸妈妈付出这么多，那我们是不是可以自豪地说一句“爸爸妈妈都爱我”？大家能标新立异，换一种方式来说一说这句话吗？（学生争先恐后地进行表达，课堂气氛逐步升温）

总结：显然，同样的一句话可以有很多种不同的表达形式，那数学中有没有这样的现象呢？今天这节课，我们主要是探索数学中这样的规律。（教师板书课题）

设计意图：将数学知识融人常见生活问题之中，可以引发学生的兴趣与好奇，使其探寻数学知识与现实问题间的本质联系。在课始，教师通过鲜活的素材触动学生的心灵，为原本冰冷的数学知识注人火热的思考，引发学生数学学习的积极心向，使后续的探究水到渠成。

数学学科的抽象性无法避免，无论是从教材设计还是从教学设计的角度来看，教师要努力拉近数学与生活之间的距离，让学生认识到数学在生活中无处不在，能够基于生活资源的支撑完成数学知识的建构与运用，这是利于学生学好数学的基本方法。学生一旦建立数学与生活关联的意识，并且形成与之相关的能力，就能够迈出数学学习坚实的第一步，这是学生数学学习走向深处的关键。

2.开放探究，建构规律

问题1：1件T恤32元，1条短裤45元，1件防晒衣65元，买5件防晒衣和5条短裤需要支付多少钱？

追问1：想要解决这个问题，应该先计算什么？再计算什么？该如何列式解答呢？请大家自主尝试解决问题。

学生进行思考，并自主尝试，很快得出算式： ①（45+65）×5=110×5= 550（元）； ②45×5+65×5=225+325=550 （元）。

追问2：谁能具体说一说自己列算式的思路？

学生阐述思路，从购物类问题模型“单价 × 数量 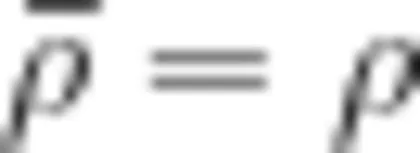总价”出发，通过混合运算完成解答。

问题2：对比这里的两个算式（45+65）×5 和 45×5+65×5 ，你有什么新的发现？

学生观察和对比后很快发现：这两个算式的结果一样；这两个算式中涉及的数也相同，有3个数，不同之处在于后一个算式中，其中一个数出现了两次；两个不同数乘同一个数相加的结果，与两个不同数相加去乘这个数的结果相同。

问题3：真是观察仔细的好孩子！居然有这么多发现。是不是可以说（2 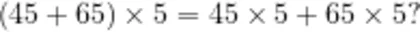这样的发现是不是巧合呢？我们是不是应该进一步举例来验证呢？

学生脑洞大开，列举出各种例子：（80+5）×2=80×2+5×2 ，算式两边都等于170； （29+11）×5=29×5+11×5？s

设计意图：在数学规律的探究中，教师要引导学生自然地发现规律，不能急于求成。在这一环节中，教师抛出问题引发学生的数学思考，当学生按照教学预设列出两个算式之后，教师并没有引导学生去发现规律，而是引导学生通过朴素的语言概括等式的特征，让“乘法分配律"知识的雏形逐步显现出来。就这样，学生在阶梯式问题的指引下进行观察、比较、举例和验证，自主构建算式模型，能实现对规律意义的个性化感悟。

对小学生而言，开放探究的过程是指让他们在充分激活生活经验的基础上，在自己的认知能力范围之内建立数学概念之间关联的过程，以及寻找问题解决思路的过程。此处教师设计的若干个问题从本质上来说就是引导学生从生活实际出发，有意识地运用数学知识去解决实际问题。正是因为教师的自然关联，才使得学生顺利进入数学探究的状态，从而充分体验数学探究的过程，并在数学问题的解决中认识到“乘法分配律”的使用场景与相关注意点。这样的探究过程可以使学生在充分运用数学知识的过程中，对数学知识形成规律性理解。

上述教学环节中有一个细节值得注意，那就是教师对学生的评价。当教师评价学生观察仔细的时候，当教师夸奖学生有不同发现的时候，实际上就是在用积极的评价激活学生的探究兴趣，发展学生的数学思维。这样的评价对学生的深度学习是一种无形且强大的助力，因此，教师在教学过程中要借助评价的力量来推动学生的深度学习。

3.分析归纳，抽象模型

问题4：这里我们所发现的计算规律，数学上称为“乘法分配律”。你能试着为它定义吗？请试着以简洁明了的语言描述这个规律。（学生自主尝试概括）

问题5：请试着表示乘法分配律。

学生深度探究后得出各式各样的表示方法：有的通过文字表示，即（甲 +（-）x 丙 =甲 × 丙 +2x 丙；有的通过画图表示，即 $（0+＼Delta）＼times＼square=0＼times＼square+$ $＼triangle＼times＼square$ ；有的通过字母表示，即 （a+b）× c=a× c+b× c 。

问题6：大家想到了如此多的表示方法，真不错！那么，这些表示方法中哪一种更简捷呢？（学生一致认为字母表示法方便简捷，应推而广之）

设计意图：教师从学生已经构建的算式模型出发，继续以问题为载体，引导学生抽象提炼算式模型中隐藏的结构性知识，促进数学模型的自然建立。正是学生深入思考和分析，不断尝试与归纳，积累学习的独特体验，才逐步提炼出有效的数学模型，顺利建立乘法分配律模型。这样的课堂学习，并非通过示范和模仿的方式进行，虽然没有出现一道数学题，但是能让学生在自主发现和创造中轻松建立终生难忘的数学模型。从发展学生数学核心素养的角度来看，这一环节涉及数学抽象与数学建模，当这些概念无法直接向学生呈现的时候，唯一有效的教学方法就是让学生经历抽象与建模的过程。这不仅可以让学生对眼前所学的知识形成深刻的认识，而且可以奠定后续数学知识学习的基础，为学生的深度学习提供可持续的力量。

4.实际应用，深化认识

问题7：填一填。（1） $（19+11）＼times4=＼square＼times4+＼square＼times4；$ （2号$（2）35＼times9+75＼times9=（＼square+＼square）＼times＼square$ 0问题8：算一算。（1） （135+25）×8 （2） 199×9+9 （3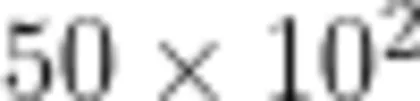） 。问题9：试着列举运用乘法分配律的实例。

问题10：试着编制一道运用乘法分配律的实际问题。

设计意图：在抽象得出模型之后，教师应适时抛出实际问题，引导学生在解决问题的过程中深化理解和认知，提升思维的灵活性、深刻性和创造性。这里，教师多方位、多角度地设计问题，引导学生去填、算、说和编，在问题解决的同时明晰乘法分配律的本质就是使计算变得简单。在这一过程中，学生储备了能量，拓宽了视野，提升了认识，完善了结构，增长了智慧。

5.课堂小结，升华认知

问题11：对于本节课的所学，你有何想法或困惑？

二、教学思考

在小学数学教学中，教师应致力于通过若干要素的有效凸显，让学生的学习过程更加匹配学生的认知规律，从而让学生在深度体验的基础上有效积累学习经验、提升学习品质，发展数学核心素养，这是当前小学数学教学的必然走向。教师要紧扣“有效"而追求“凸显”，追求教学结果与过程的有机关联。在此过程中，教师应努力做到以下两点。

1.凸显知识的生长点，为建构新知提供支持

乘法分配律是乘法教学的延伸与扩展，教师应联系学生已有的知识与经验，引导学生在解决实际问题时经历规律探索的全过程，从而自主发现和归纳乘法分配律。学生学习过四则混合运算，对“乘法分配律”的相关内容有一些了解。在本节课中，教师从教学内容出发，基于学生的已有知识基础设计活动，尤其注重新旧知识的联系与意义沟通，充分凸显知识的生长点，让学生自然建构知识体系。从整节课的推进不难看出，教师有效凸显知识的生长点，引导学生进行观察、比较和归纳，让学生自然地发现乘法分配律。教师让学生站在探究主体的位置上，将数学思考聚焦在此处，为学生自主建构乘法分配律模型提供实实在在的支持。

2.凸显教学的重点，深化学生的理解

让学生掌握乘法分配律的计算方法，并能得心应手地进行计算，是本节课的教学重点。其中，让学生亲历乘法分配律的探究过程是教学的难点。虽然学生已经具备了乘法运算的能力，但让学生主动建构知识，突破教学的重难点有难度。在本节课中，教师设计了让学生自主发现和探究规律的教学环节，有效凸显了教学的重难点，深化了学生的数学理解。正是因为学生有自主探究的时间与空间，有畅所欲言的学习环境，才使得自身的数学思维不断得到锻炼，对“乘法分配律"的理解从表象走向本质，清晰且深刻。

综上所述，在小学数学课堂教学中，教师必须深入解读教材、分析教学内容、了解具体学情，精准把握教学目标，有效凸显知识的生长点和教学的重难点，凸显教学的基本要点，这样才能将学生的数学学习引向深处，让学生深人理解数学知识，能够在更高学习品质的支撑下实现学生数学核心素养的全面发展。