基于推理意识发展的数学教学实践与思考
作者: 刘楠[
逻辑推理是指以生活实际或一些命题为起点,根据一定的规则推导其他相关知识或命题的过程。推理是抽象数学结论的重要途径,其表现形式主要有特殊到一般的合情推理与一般到特殊的演绎推理。根据小学阶段学生的身心发展特点来看,学生正处于推理意识发展的高峰期,教师应抓住这个关键期,想方设法引导学生主动猜想并验证,从真正意义上为发展学生的数学核心素养奠定基础。笔者以“多边形的内角和"教学为例,谈谈推理意识的培养。
一、逻辑推理的重要价值
教师要以学生已有的认知水平和学习经验为教学的起点,通过理论联系实际,贯彻并落实新课改的指导思想,为发展学生学习能力创造条件。小学数学教学不仅要关注学生对知识与技能的掌握程度,更要关注学生推理意识的发展情况,此为提升学生综合能力的基础[1]。小学生的心智仍在发展期,其认知结构中的知识难以支撑当下的数学问题。为了发展学生思维的严谨性,教师在教学过程中要加强引导,让学生学会从逻辑推理入手实现深度学习。
二、实践措施
1.类比导入,建构概念
导入环节,教师借助多媒体展示几幅有不同几何图形的生活实物图,让学生通过对图片的观察,发现生活中除了三角形,还存在其他几何图形,由此引出对多边形的初步感知。在此基础上,教师引导学生先回顾三角形的定义,然后仿照三角形的定义为多边形下定义。在学生描述过程中教师要加强引导,逐步完善学生对“顶点”“内角""边""对角线"等概念的理解。
师:大家还记得在探索三角形的定义后,又研究了三角形的什么内容?
生1:探索了三角形的边和角。
师:本节课我们探索的主题为多边形,那么在获得其定义之后,将会研究多边形的什么内容呢?
生2:应该是探索多边形的边与角。
师:不错,本节课我们将着重分析与多边形的角相关的问题一一多边形的内角和。
设计意图:教师将生活情境作为教学的切人口,让学生从各种图片中感知多边形的客观存在,对多边形形成初步感知,通过类比三角形获取其定义,并为明确研究方向、揭示课题奠定基础。这样设计遵循了学生认知发展由浅人深的规律,因为三角形是学生所熟悉的图形,以此作为类比的基础,更能提升学生的理解能力,为学生形成系统化的认知结构做好铺垫。
2.多维思考,转化理解
问题1:在以前的学习中,大家已经明确了三角形的内角和是 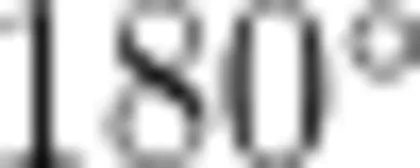 ,那么有没有同学知道长方形的内角和是多少度?
,那么有没有同学知道长方形的内角和是多少度?
生3:鉴于长方形的4个角均为直角,它的内角和就是 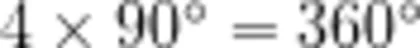 。
。
师:分析得很有道理,长方形属于一种特殊的四边形,它的内角和是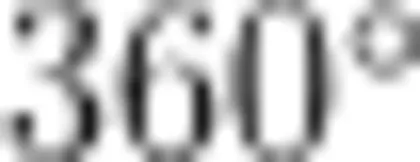 ,那么一般的四边形内角和是不是
,那么一般的四边形内角和是不是 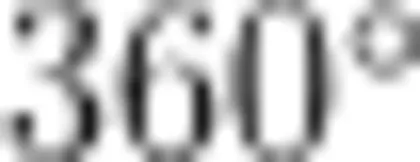 呢?
呢?
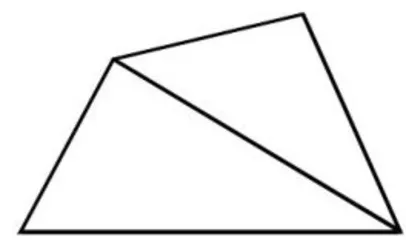
生4:如图1所示,画一个任意四边形,连接四边形的两个顶点,可将四边形分割成两个三角形,根据以前的学习,确定一个三角形的内角和为 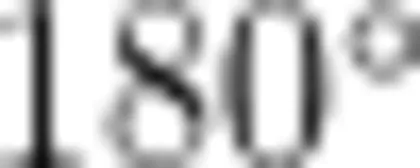 ,两个三角形的内角和必然为
,两个三角形的内角和必然为 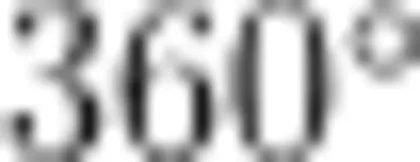 ,由此可知一般四边形的内角和为
,由此可知一般四边形的内角和为 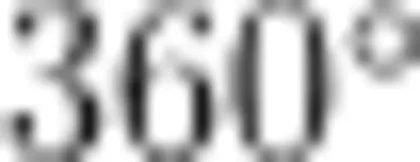 。
。
师:很好!除了将一个四边形转化成两个三角形之外,还有其他转化方法吗?
教师鼓励学生先独立思考,再交流并展示自己的思路。随着不同方法的探索,学生总结:不论用哪种方法来验证四边形的内角和,其本质都是将四边形转化成三角形来分析,这里的四边形内角和属于未知,而三角形内角和则属于已知,因此均为“化未知为已知"的过程,即将一个原本复杂的问题转化成简单的问题来分析。
设计意图:三角形属于数学基本图形,四边形属于多边形的起点,学生一旦明确四边形内角和的研究思路,后续无论几边形的内角和都有了方法基础。此为学生活动经验的探索与积累过程,一切均为探索 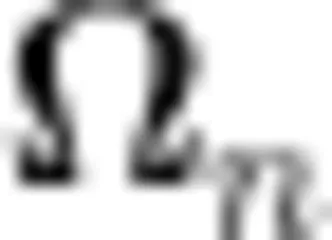 边形内角和而形成一般化的结论做好铺垫。此环节教师引导学生应用了独立思考、合作、展示与交流等学习方式,让课堂在多元化的教学模式下动态生成。学生在探索中不仅体会了将四边形转化为三角形的不同分割法,还亲历了“特殊到一般""转化"等思想方法,实现了“猜想一验证""合情推理一演绎推理"的转化。
边形内角和而形成一般化的结论做好铺垫。此环节教师引导学生应用了独立思考、合作、展示与交流等学习方式,让课堂在多元化的教学模式下动态生成。学生在探索中不仅体会了将四边形转化为三角形的不同分割法,还亲历了“特殊到一般""转化"等思想方法,实现了“猜想一验证""合情推理一演绎推理"的转化。
3.深入探索,逻辑论证
师:关于多边形内角和的探索方法较多,你们觉得哪种方法最简便?
生5:还是直接连接对角线的方法最便捷。
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:sxjz20250319.pd原版全文
师:确实,现在请大家结合以上探索经验,分别分析 5,6,7,?s n 边形的内角和分别是多少,并将结论记录到表1中。
教师将学生不同的证明方法进行展示,并鼓励学生将逻辑证明过程阐述清楚,顺利推导出 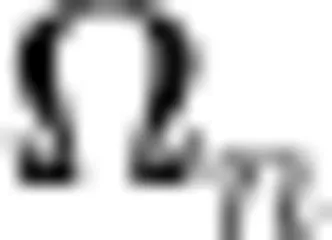 边形内角和的公式为
边形内角和的公式为 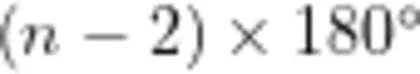 。
。
师:关于公式 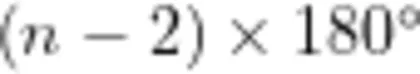 ,你们有什么想法?
,你们有什么想法?
教师要求学生先交流,再展示想法。学生提出的想法有四类: ① 根据多边形边的数量可确定内角和; ② 反之,基于多边形内角和可确定是几边形; ③ 多边形的内角和必定为 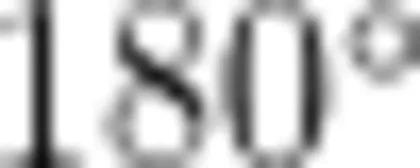 的倍数; ④ 多边形每增加一条边,其内角和就增加
的倍数; ④ 多边形每增加一条边,其内角和就增加 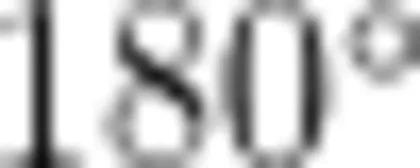 。
。
设计意图:直观操作与逻辑推理的深度融合,让学生有机会亲历实验、观察、分析与思考的过程,使其获得的结论更加丰富,这对提升学生的演绎推理意识具有重要价值。
4.例题解析,夯牢基础
例1:已知某个多边形的内角和是 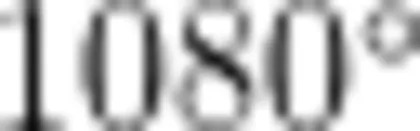 ,分析此为几边形?
,分析此为几边形?
例2:如图2所示,已知四边形A B C D 内的∠A与 ∠ C 互补,则 ∠ B 与 ∠ D 之间是怎样的关系?说明理由。
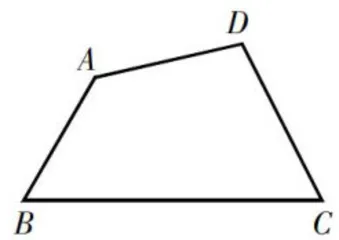
通过以上两个例题的探索,学生发现在一个四边形内,如果一组对角互补,则另外一组对角同样互补。为了进一步深化学生的理解,巩固并夯实学生的知识基础,教师继续提出拓展题,鼓励学生自主探索。
拓展题:如图3所示,已知四边形 A B C D 中的 ∠ A 与 ∠ C 为互补的关系, ∠ A D C 与 ∠ A B C 的角平分线分别与 A B,C D 边相交于点 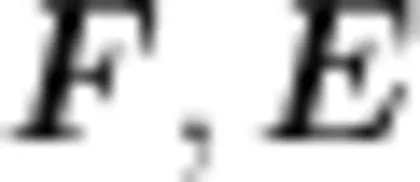 那么图中的 ∠1,∠2 之间是怎样的关系?说明理由。
那么图中的 ∠1,∠2 之间是怎样的关系?说明理由。
关于本题,教师要求同桌之间进行讨论,并随机抽取学生展示解题思路。在此基础上,教师设计了几道练习题供学生思考。

练习1: ① 下面四个结论,哪一个不可能为多边形的内角和?
A. 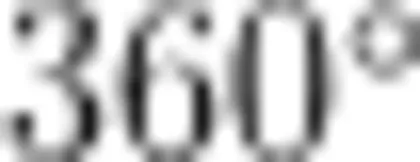 ;B.
;B. 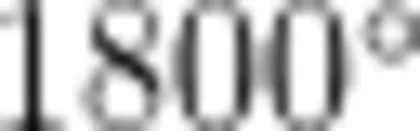
C. 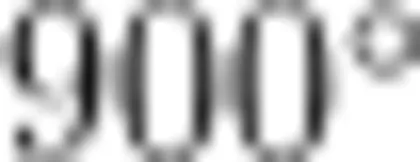 ;D.
;D.  。
。
② 十一边形的内角和度数是。③ 已知某个六边形的各个内角度数均一样,则各个内角的度数是。④(n+2) 边形的内角和与 n 边形的内角和相比,相差度。
练习2:分别求图4中的 x 值。
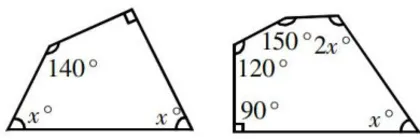
设计意图:经典例题的应用,能进一步巩固学生对多边形内角和公式的应用意识;拓展题的应用,意在让学生学会从复杂的关系中洞察多边形内角和的本质;巩固练习由学生自主完成,可让学生夯实基础知识,积累学习经验,为后续探索更多的综合性问题做准备。此环节的例题、拓展与练习,均起到巩固知识与强化意识的作用。
5.课堂总结,提炼升华
课堂尾声,教师要求学生以小组合作的方式,分别从如下几个方面进行思考与总结:关于多边形内角和的探索,大家经历了怎样的过程?有哪些收获?存在什么困惑?尝试为本节课的教学提一个问题。
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:sxjz20250319.pd原版全文