单元整体视域下的复习教学实践与研究

随着新课改的深入推进，利用学科教学发展学生的核心素养为教育界公认的目标。以什么来评判学生的核心素养发展程度呢？实践表明，学生能否在数学学习中建构系统化的认知架构，形成结构化的思维体系，获得必备品格与关键能力等，为基本评判标准。基于单元整体视域设计教学是一种着眼于知识内部逻辑关系，立足于某一核心思想，重组或整合教学内容，形成一种相对完整且动态的教学模式。因此，教师在单元整体视域下进行数学教学设计，对培养学生的数学核心素养具有重要价值。

一、复习教学现状分析

复习教学关键性的作用在于巩固学生已学的知识，通过复习掌握知识间的内部联系与逻辑结构，为学生形成结构化的思维与认知架构创造条件。然而，当前小学数学复习教学受教师教学理念或教学行为的影响，存在“三重三轻"现象：重知识再现，轻融会贯通，学生处于碎片化复习状态，无法建构完整的知识结构网；重练习训练，轻拓展延伸，学生的思维一直处于浅表层面，无法达到深度学习的境界；重知识整理，轻思想方法，学生因为缺乏反思，导致课堂学习流于形式。

二、教学过程设计

1.知识勾连，思辨融通

授新课时，学生要探索的知识是以前没有接触过的，因此教师会将新知"揉碎了"让学生“消化吸收”，导致学生在课堂中掌握的知识点具有碎片化特征。日积月累，学生大脑中知识点越积越多，这就给理解与记忆带来较重的负担。复习教学就是基于整体视域，引导学生将这些碎片化知识编织成一张便于理解的知识结构网，促使学生通过复习获得具有“生长性"的知识结构[1]。教学时，教师要引导学生做好知识的联系，让学生从自身实际认知需求出发，在丰富的情境与问题中不断提升认知，对知识的内在关联性产生明确认识，从真正意义

上实现思辨融通。

师：通过多边形面积公式的整理，我发现各个多边形面积公式之间存在一定的内在关联，请大家尝试用导图的方式来揭示这种关联。

学生自主画图并分析，在合作交流的基础上，最终形成以平行四边形为核心的导图形式（见图1所示）。

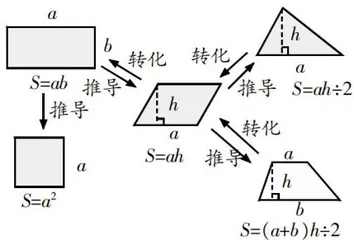
师：通过对图1的观察，请大家说说各个公式之间的转化涉及哪些数学思想方法。

生1：显而易见，就是应用了数学转化思想，即将探索的新知转化为旧知，再以旧知为出发点，推导出新知，此为新旧知识联系的过程。

师：假设我们在解题时，不记得梯形的面积公式了，该怎么办呢？

生2：可以临时分割梯形，即将它切割成"两个三角形"或“一个平行四边形和一个三角形”。

生3：还可以想办法把梯形补成一个长方形，然后以减法求得梯形面积。

师：以上方法涉及研究数学问题常用的“割”与“补”，割补的目的是什么？

生4：为了将未知面积的梯形转化成更容易求得面积的基本图形。

师：由此可见，数学转化是一种重要的思想方法。现在请大家观察图2，思考：借助梯形的面积公式可否获得三角形与平行四边形的面积？

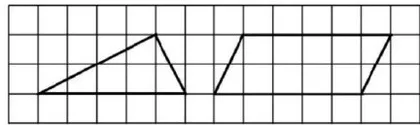
生5：可将图中三角形理解为一个梯形，其上底为0，下底为5，高为2，如此即可用梯形面积公式获得三角形面积，即 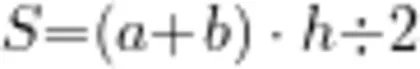中的 a= 0，那么梯形的面积经转化后，就变成S=（0+b）？ h÷2=b？ h÷2 ，此为三角形的面积计算方法。

教师借助几何画板演示三角形与梯形互相转变的过程。

师：非常好！借助梯形面积公式大家顺利获得了三角形的面积，那么如何借助梯形公式获得平行四边形的面积呢？

生6：可将图中的平行四边形视为上底、下底均为5，高为2的梯形

生7：或将它视为上底、下底相等的梯形。

教师用几何画板展示梯形与平行四边形互相转化的过程。

师：现在用梯形的面积公式探索平行四边形的面积，具体该怎么处理？

生8：“梯形"的上底、下底均用 a 表示，将其代入梯形面积公式中，即S=（a+b）？ h÷2=2a h÷2=a h ，自然形成平行四边形的面积公式。

师：不错，以此类推，大家能否用梯形的面积公式来探索一个长方形的面积呢？

生9：当然可以，即将问题理解为梯形的邻边之间为垂直的关系，上底、下底等长，那么长方形就成了一个特殊的梯形。

师：很好！以上借助梯形面积分别探索三角形、平行四边形以及长方形面积的过程，大家有什么感悟？

生10：将梯形面积公式分别应用到三角形、平行四边形以及长方形的探索中，可自然而然地转化为各个图形相对应的面积计算公式。

生11：看似毫不相关的内容之间，竟然有一定的内在联系。

设计意图：在教师引导下，学生自主梳理多边形的面积公式，为完善认知结构奠定基础。教师引导学生经历推导梯形面积，以及用梯形面积公式分别求其他图形面积的探索过程，能实现图形变化与公式转化的推演，让学生从不同维度感知多边形面积公式之间的关联性。如此设计，不仅能帮助学生厘清知识点，还能帮助学生突破思维定式，实现知识的勾连与思辨融通。

2.拓展延伸，拔高思维

单元复习的任务不仅是让学生回顾旧知，更重要的是发现知识漏洞，查漏补缺，拓展思维，生成智慧。比如，在“多边形面积计算"的复习教学时，教师可以开展拓展延伸活动。

师：李大伯准备在一块平行四边形的田里画一个最大的三角形图案，该怎么操作？

生12：画出来的三角形底即平行四边形的底，顶点位于平行四边形的另外一条底边上。

师：由此获得的最大三角形数量有多少？

生13：有无数个。

如图3所示，教师用几何画板演示无数个满足条件的三角形。

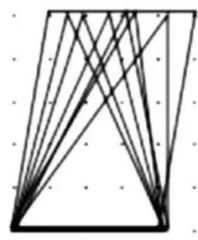
师：如果换一个方向，取两个最大的三角形，那么所获得的三角形面积之间存在怎样的联系？

生14：如图4所示，不同方向截取的最大三角形面积为相等的关系。因为所截取的两个三角形与平行四边形具有等底等高的特点，那么其面积均为平行四边形面积的

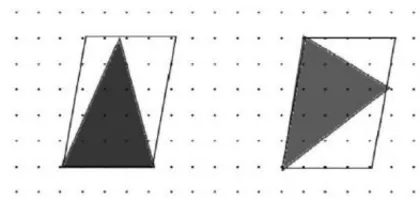
师：如果到平行四边形的外面找三角形，可以画出多少个与“平行四边形内部最大三角形面积"相等的三角形？

学生一致表示可以画出无数个满足条件的三角形，教师借助几何画板进行演示。在学生对此产生明确认识的基础上，教师要求学生观察图5，连接图中梯形的对角线，分析涂色部分的面积。

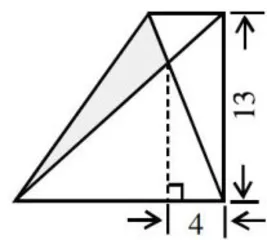
学生结合自身已有的认知经验开展分析，发现图中左半边的三角形面积与右半边三角形的面积相等，只要求出右半边三角形面积，就很容易获得左半边涂色部分三角形的面积，列式为 13×4÷2=26 。

设计意图：完善学生的知识体系是复习教学的基本目标。此外，教师要适当进行拓展延伸，以增强知识的宽度与深度，为学生实现深度学习创造条件。此环节，教师通过对习题潜在价值的探索，挖掘处于学生认知“最近发展区”的问题，引发学生的思考，达到巩固复习与启迪思维的目的。

3.反思提炼，发展素养

知识的梳理与体系的建构是单元复习的主要任务。复习教学时，教师要引导学生进行反思，达到优化其思维和发展其核心素养的目的。

师：本节课，关于多边形面积公式的复习应用了哪些方法？这些方法中，有哪些是大家以前很少接触的？

生15：我们梳理了各种多边形的面积公式，其中用梯形面积公式来探索其他图形面积公式是以前没遇到过的。

师：由此带给你们什么感悟？

生16：数学知识并非独立存在的个体，各个知识点之间可能存在一定的联系。

生17：令我意外的是一个问题中竟然可以蕴含大量的知识，今后解题不能太随意，一定要严谨，多思考。

生18：通过本节课的学习，我发现数学转化思想对解决数学问题具有重要作用。

师：看到大家通过本节课的复习收获满满，我感到很欣慰。学无止境，在今后的学习中，我们一定要学会深入探索、用心思考，要主动参与学习，尤其要获得良好的“提问"能力，此为促进个体成长的关键。

设计意图：在反思总结环节，教师并没有将所有的目光锁定在知识与技能层面，而是引导学生从思想方法、探索经验、能力发展等维度去感知、体悟，从真正意义上推进学生学习能力的发展。如此设计，对培养学生核心素养具有重要意义，对学生形成可持续发展的能力具有重要价值。

三、思考与感悟

1.完善知识结构是复习教学的基础

何为复习？复习就是在学生已有认知经验基础上，教师进一步梳理知识点，根据知识内部逻辑关系设计教学活动，让学生在复习中逐步对知识间的关联产生明确认识，为形成系统化的认知奠定基础，以从真正意义上完善知识结构。部分教师没有关注到知识融会贯通的重要性，复习时仍以单个知识点开展教学，这就严重阻碍了学生知识结构的形成，导致学生后续综合应用时无法灵活变通。

本节课的复习主题为多边形面积公式的计算，涉及的图形比较多，想要完善学生的知识结构，最好的办法就是将各种多边形罗列到一起，以导图的方式将各个图形面积之间的关系总结出来，如此则能顺利实现知识的融会贯通。

2.适度拓展延伸是复习教学的核心

与新知教学相比，复习教学对学生知识掌握程度要求更高。为了增强知识的宽度与深度，在单元整体视域下的复习教学时，教师要关注问题的拓展延伸，让学生获得举一反三的能力，提升其核心素养。从本节课的教学来看，第一个教学环节，教师已经与学生一起探索了基础知识，帮助学生建构了知识结构；第二个教学环节，在学生已有认知经验基础上，教师将问题进行了拓展延伸，进一步激活了学生的思维，让学生对多边形面积问题产生深刻理解，并感知数学转化思想的重要性，从真正意义上抵达深度学习的境地。

3.及时反思提炼是复习教学的 关键

对于复习教学来说，教师要引导学生进行反思，及时反思可以让学生审视自身的学习状态以及对知识的掌握情况。在本节课的总结反思环节，教师以基础知识为起点，循序渐进地将学生引入对方法、学习能力、素养等方面的反思，让学生对多边形面积的认识实现感性向理性的转变，此为学生学习能力发展的表现，对发展其核心素养具有重要意义。

总之，教师要改变复习教学“高耗低能"的现象，对教学内容要有整体的认识，了解学生的现实起点，系统整合教学内容，做到教学有针对性[2]，逐步提升学生的认识水平，帮助学生建构完整的知识结构。

参考文献：

[1］李雪峰.让单元复习课更具生长的力量：以“多边形的面积计算整理与练习”为例[J]：小学数学教育，2021（24）：15-16.

[2］林婕纯.基于单元整体教学的核心课例研究：以“除法的初步认识"为例[J]．小学数学教育，2021（Z3）：17-20.