协变思维在小学数学教学中的应用研究

思维是学生认识并理解数学的原动力与基本工具。教师在教学中将知识的传授与思维能力的培养有机融合在一起，是发展学生数学核心素养的重要举措。协变思维属于数学思维中的一种，对提升学生的认知能力和解题能力具有重要意义。

一、协变思维的概述

协变思维也称协同变化思维，属于众多数学思维的一种，指将情境中两个有一定关系的量放在一起进行互相转化的一种思维[1。教师可以从三个方面引导学生认识协变思维：① 协变思维属于认知活动的一类；② 涉及协变思维的量属于同一情境中有一定关系的变量； ③ 从本质上来说，协变思维属于函数思维。

二、学生的协变思维现状分析

问题1：小明与小慧共有16颗巧克力，小慧吃掉2颗后，两人拥有的巧克力数量一样多。求两人原来各有几颗巧克力。

问题2：小明与小慧共有16颗巧克力，小慧给了小明2颗巧克力后，两人拥有的巧克力数量一样多。求两人原来各有几颗巧克力。

为了充分了解学生的协变思维情况，笔者分别让三年级与四年级的学生来解决这两个问题。调查发现，关于问题1，三年级、四年级的学生错误率分别为 8% 与 2% ；关于问题2，三年级、四年级学生的错误率分别为 83% 与 61% 。显然，问题2的错误率远高于问题1，低年级的学生错误率高于高年级学生。出现这种情况的主要原因在于问题2的数量关系比较复杂，具有变化性，学生无法像问题1一样快速理解；随着认知的发展，学生的协变思维越来越强。实践证明，大部分学生习惯用直觉思维分析问题，缺乏良好的协变思维能力。

三、剖析学生协变思维能力不足的原因

1.对于量的认识不足小学阶段的数学问题涉及连续与分散两类量，连续量包含了面积、质量、长度、时间等，分散量有人数、物品数量等。解决实际问题时，学生因为对一些量的理解不充分，出现思维混乱，导致解题错误。

比如，从教学楼的一楼跑到五楼，小红需要花费1分钟的时间。按照这样的速度，她从一楼跑到十楼需要花费多少时间？此问中的“一楼到十楼"并非为具有离散意义的物品的数量，而是具有连续意义的量—长度。简而言之，一楼到五楼表示四个单位长度，一楼到十楼表示九个单位长度。学生基于协变思维的视角认识到这一点，问题则迎刃而解。

这个问题学生出现的错误率很高，主要原因就在于协变思维能力不足，对事物的量没有形成客观、科学的认识。想要解决这个问题，教师要在日常教学中注重引导学生对事物的量的分析，让学生学会从整体视域来观察事物。

2.缺乏协调转换能力

有些学生虽然能明确量的性质，但在解决问题过程中缺乏良好的协调转换能力，导致出现各种错误。

如图1所示，分别用4、7、10根小棒可摆放出1、2、3个正方形。如果想按照同样的方法摆放出100个正方形，要用多少根小棒呢？此问中正方形的个数与小棒的数量为两个关联的变量。正方形数量的3倍加1为所需小棒的数量；反之，小棒数量减1，再乘以 为正方形的个数。

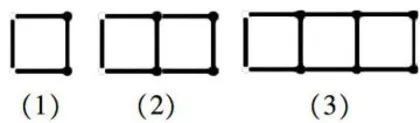
然而，不少学生在解决这个问题时，难以灵活转化这两个变量，出现各种错解。想要改变这一现象，最好的方法就是增强对学生协变思维的训练，让学生学会从题干条件中提取有关联的变量，并明晰变量间的关系，获得从正反不同维度转换的能力。

3.不善于利用比例关系

问题中的比例关系反映了特殊的协变思维。然而，部分学生对正反比例关系的理解与认识存在障碍，难以准确应用比例关系解决实际问题。比如工程队准备修建一条1200米的柏油路，前3天完成了总长度的1/3，（2如果以同样的进度继续工作，还要用几天的时间可以完成整个修建工程？

本题难度系数并不大，拥有一定协变思维的学生都能根据已完工与未完工路程的比例1：2，得出剩下的路还需要花费6天的结论，这种解题方法快捷、方便。然而，缺乏协变思维的学生会分别求出平均每天修建路程长度以及剩下路程的长度，通过除法获得剩下路程需要花费的天数。这种解法虽然能获得结论，却复杂许多。协变思维的介入，可简化问题难度，让学生快速得出问题的结论。

四、应对措施

1.教学分析

笔者以“平行四边形的面积"教学为例，从学生实际认知水平出发，开展教学实践与分析，以培育学生的数学协变思维。

问题：已知一个平行四边形的底边长为7厘米，底边上的高为4厘米，另一条边的长度为5厘米，求该平行四边形的面积。

本题是在认识平行四边形之后，初次让学生自主计算面积的一个问题，从学生的解题结果来看，不少学生直接应用“邻边相乘"的方法进行解题。显然，学生对平行四边形中量与量之间关系的理解还不够准确。

教学时，大部分教师基于转化思想引导学生开展探索，尤其关注不同剪拼法的应用与分析。实际上，沿着不同的高对平行四边形进行剪拼，并非本节课教学的难点，原因在于学生在“认识图形”环节曾多次接触过这一类操作，大部分学生都能理解。因此，以剪拼法探索面积公式的难度较小。

那么，此环节的教学难点究竟在哪里呢？从封闭图形来分析，面积与周长为这一类图形的两个量，且封闭图形的面积与周长之间还存在双量协变的关系，不论面积还是周长均与图形的长、宽、高有关联。教师只要引导学生真正理解了这些关联的规律，就能发展学生的协变思维。

基于以上分析，本节课笔者紧扣问题提供的数据开展研究，通过问题发散学生的思维，让学生明晰如何计算平行四边形的面积。当然，本节课教师要引导学生通过探索面积与周长的协变关系，揭示周长相同的图形，面积并不一定相同；周长越大的图形，面积不一定越大等。为了深化学生的理解，教师可以从“关联量的变与不变"的角度开展教学。

2.教学过程安排

（1）公式推导

教师可以从三次变化着手，引导学生进行平行四边形的公式推导。

第一次：将不规则图形转化为规则的长方形，但面积不发生变化。

如图2所示，教师可以引导学生应用“割补法"进行操作，让学生感知割补过程与要点，从而深刻领悟：将图形进行割补，面积不会发生变化，但周长与图形形状会发生显著变化。

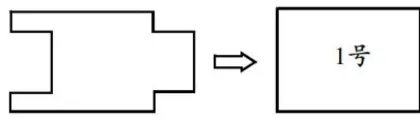
第二次：如图3所示，通过对图中1号图形的拉动，将长方形转化为平行四边形，具体分成两个步骤。

第一步，通过拉动，使得平行四边形的高为 4cm 。教师要鼓励学生自主操作，并说明在此过程中哪些量发生了改变，哪些量没有发生变化。

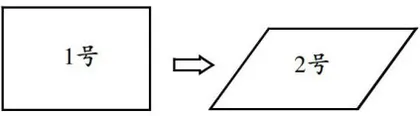
有的学生认为图形经过拉动，各条边的长度没有发生变化，因此变化的只是图形形状，周长与面积均未发生改变。教师未置可否，而是要求学生继续操作。

第二步，继续拉动图形，使平行四边形的高逐渐变为 $3＼mathrm{cm}＼ 、2＼mathrm{cm}$ lcm，要求学生说明在拉动过程中哪些量发生了改变，哪些量没有发生变化。

随着高的逐渐减小，学生逐渐意识到虽然各边的长度没有发生变化，但图形的面积越来越小，其周长始终没有改变。由此，学生猜想到平行四边形的面积与其高有直接关系。值得注意的是，这里存在两个容易混淆的量，即底边的高和相邻的边。

在教师的引导下，学生自主操作并观察，通过比较与分析后发现：底边的邻边始终没有发生改变，但底边上的高逐渐变小。由此学生初步确定平行四边形的面积由平行四边形的底边与底边上的高决定，与底边的邻边没有关系。这一认识，为学生接下来推导面积公式夯实了基础。

第三次：将平行四边形转化为与之面积一样大的长方形，即将图4中的2号图形转化成3号图形，鼓励学生自主分析用哪种方法进行操作。

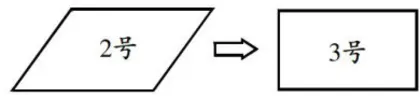
在问题的驱动下，学生分别从割补法与拉动法两个维度进行合作交流后发现：应用割补法，图形的形状发生了改变，周长与一些边的长度也变了，但面积不会发生改变；应用拉动法，图形各条边的长度没有发生改变，周长也不会发生变化，但图形的面积发生了变化。由此确定，割补法可实现等面积转化，拉动法无法满足要求。由此，平行四边形的面积公式浮出水面。

设计意图：不一样的转化过程，让学生对“等积变化"与“等长变形”

产生深刻的认识。如此设计，除了为“等积变形推导平行四边形的面积公式"作铺垫，还让学生通过操作与思考自主规避“底边 × 邻边"这一错误方法，由此形成良好的协变思维。学生自主意识到平行四边形的面积不可用“底边 × 邻边”，将注意力转移到“等积变形"中来，即关注平行四边形的底边与高这两个量之间的联系，顺利完成面积公式的推导。显然，这三个层次清晰的变化过程，让学生对边与边、边与高、边与周长、高与面积之间的关系产生了明确的认识，有效促进了学生的协变思维的发展。

（2）巩固练习

在巩固练习环节，教师可以从两次变化着手开展探索。

第一次：如图5所示，借助橡皮筋、钉子板等工具，分别围成与图4中2号图形等底等高却不同形状的平行四边形，学生通过对这些图形面积的计算，分析有哪些量发生了改变，有哪些量恒定不变。

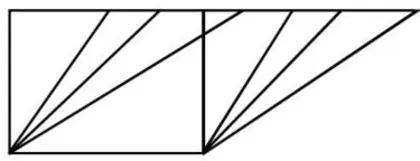
学生通过交流发现：虽然围成的图形形状发生了变化，有些边长发生了变化，但根据面积公式计算出来的图形面积恒定不变，并发现底边的邻边边长越大，该边与底边形成的夹角就越小。只要保持底边与高不变，那么不论图形形状怎样变化，面积均不会发生改变。由此，进一步强化了学生对平行四边形底边与高关系的认识。

第二次：教师引导学生自主计算图6中平行四边形的面积之后，要求学生思考问题。

问题1：为什么大家都用 12×15 而不是用 18×15 来计算平行四边形的面积呢？

问题2：如果将长为18的这条边作为平行四边形的底，与之相对应的高是多少？

问题3：与图6中图形面积一样的其他平行四边形的底、高分别是多少？如果明确底边分别为30或20，高呢？

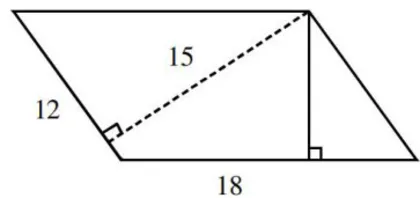
设计意图：教师引导学生通过对问题的探索，让学生进一步夯实对平行四边形面积公式本质的认识，对平行四边形底与高的关系有深刻理解，发展学生的数学协变思维。

总之，数学是思维的体操，思维是学生认识数学、掌握数学知识的动力、工具和武器，关注学生数学协变思维的培育是发展学生数学思维的基础[2]。教师应引导学生厘清问题条件中不同量之间协调变化关系，鼓励学生学会从不同的维度来观察与剖析各个量之间的关系，此为发展学生的数学协变思维的关键措施。

参考文献：

[1］尤善培.基于思维发展设计教学路径：再谈着眼于学生思维发展的数学教学设计策略[J].高中数学教与学，2015（23）：1-4.

[2]严兵.协变思维能力缺失的原因分析与教学应对：以“平行四边形的面积"教学为例[J].小学数学教育，2020（12）：20-22.