从定性到定量，关注知识的生长

小学生主要是在情境中认识平面图形，在探索中建构特征，在建构中提升思考，在活动中发展观念。这是一个从显性认识到隐性认识的过程，能促进学生在抽象中学会用图形和语言表征平面图形。笔者在教学“长方形和正方形的认识”一课时，设计了丰富的动手和动脑活动，先让学生整体感知长方形和正方形的模样，再在定性描述和定量刻画中认识长方形和正方形的本质特征。

一、旧知引入，直观认识长方形和正方形

学生在一年级时就认识了长方形和正方形等平面图形，到三年级时通过边和角等元素进一步刻画长方形和正方形等平面图形，逐步从感性认识上升到理性认识，从直观感知上升到抽象认识，从整体认识过渡到局部细化。在教学导人时，教师要从学生的旧知引人，引导学生观察长方形和正方形的特征，为理性验证这些平面图形做好准备。

师：同学们，谁来说一说四边形有什么特点？

生1：四边形有四条边和四个角。

师：大家想一想，在生活中有哪些常见的四边形？

生2：正方形、长方形、平行四边形、梯形、菱形。

师：我们在一年级时已经认识了长方形和正方形，回忆一下它们是什么样子的？请用学具袋中的材料表示长方形和正方形。

师：（出示学生的长方形作品）这些图形的颜色和大小都不相同，为什么它们都是长方形？

生3：因为长方形对边相等，就是左边和右边相等，上面和下面相等。还有长方形的四个角都是直角。

师：（出示学生的正方形作品）这些图形的颜色和大小也不相同，为什么它们都是正方形？

生4：因为正方形四条边都相等，四个角都是直角。

在这个教学片段中，教师引导学生整体感知长方形和正方形，概括出长方形和正方形的特点，发现长方形和正方形都是由四条直边和四个直角组成的，唤醒了学生对四边形的已有经验。

二、理性验证，定性描述和定量刻画图形

定性描述和定量刻画都是学生认识图形过程中的必经之路。定性描述是指从宏观角度认识事物的总体属性和趋势，定量刻画是指从微观角度用精确的数据来描述事物。当学生了解长方形和正方形的基本特征后，教师通过折纸等活动引导学生验证长方形和正方形的特征。学生使用不同的长方形和正方形纸进行量一量、折一折和比一比，以验证长方形和正方形的边和角的特征，最后在沟通中明确：长方形有四条边，对边相等；有四个角，都是直角；正方形的四条边都相等，四个角都是直角。

1.理性验证长方形的特征

师：刚才我们是用眼睛看到的，接下来要验证你们的发现是否正确？

请拿出一个长方形验证其四条边和四个角的特征。

生1：我是用左右对折和上下对折的方法来验证长方形的对边相等，再用三角尺中的直角验证长方形的四个角都是直角的。

生2：我用尺子量出长方形的左边和右边都是13厘米，上边和下边都是8厘米；再用三角尺的直角来验证四个角都是直角。

师：我们通过量一量、折一折和比一比等方法验证了长方形边和角的特点，发现长方形要同时满足对边相等和四个角都是直角的特点。在课前，每个同学都制作了一个长方形，请动手验证一下你们亲手制作的到底是不是长方形。

生3：我发现我这个图形不是长方形，我用三角尺测量了两个角，发现它们比直角要小一点点。

生4：我用直尺测量了我这个图形的左边和右边都是10厘米，上面和下面都是7厘米3毫米，所以我确定这个图形就是长方形。

生5：你们组为什么不测量这个图形的四个角，还要四个角都是直角才能确定它是长方形。上下两条边一样长，左右两条边一样长，平行四边形也是符合条件的。

师：是的，所以我们在验证长方形时要同时满足两组对边相等和四个角都是直角这两个条件。

2.理性验证正方形的特征

师：刚才同学们用不同的方法验证了长方形，现在我们来研究正方形，正方形有什么特点？大家用什么方法来验证自己的发现呢？

生6：我是用直尺量出正方形的四条边，经过测量这四条边都是8厘米5毫米，说明正方形的四条边都是一样长的；再用三角尺量出正方形的四个角，经过测量这四个角都是直角。所以这个图形是正方形。

生7：我先确定这个图形是不是对边相等，用上下对折和左右对折的方法发现能完全重合，再测量相邻两条边的长度，只要相等就说明四条边相等；然后，通过上下对折和左右对折这个图形，让四个角都重叠在一起，只要用三角尺测量一个角是不是直角就行了。

生8：我们是把正方形沿着对角线对折两次，让正方形的四条边都重叠在一起，只要测量一次就行了。

生9：我们组是用小棒拼搭的，可以拆下一根小棒，与其他三根小棒比一比长度可以验证边长是否相同，再用三角尺测量一个角是不是直角。

师：现在我们通过验证发现正方形要满足四条边相等和四个角都是直角这两个条件。在课前，每个同学都制作了一个正方形，请动手验证一下自己制作的是不是正方形？

生10：我是在方格纸上画了一个正方形，每条边的长度是5厘米，四个角都是直角，所以是正方形。

生11：我用直尺量出每条边的长度都是相等的，再用三角尺量出四个角都是直角，所以这个图形是正方形。

在这个教学片段中，学生通过量一量边的长度和角的度数，左右对折和上下对折，将观察得到的猜想通过理性的验证得出正确的结论，最终得到判断长方形和正方形的理论依据。在理性验证的过程中，有的学生只验证了“边"而忽视了“角”，在学生的质疑和举反例中进一步深刻理解长方形和正方形都要同时满足“边”和“角"这两个条件。

三、拓展提升，借助活动探究图形的关系

当学生经历从物的具象到形的抽象过程后，教师设计了三个拓展练习题，引导学生深刻感知四边形、长方形和正方形之间的图形关系，发展学生的空间观念。教师通过让学生比较长方形和正方形的特征，体会不同四边形的联系和区别，并在此基础上揭示长方形的长、宽及正方形的边长等概念。

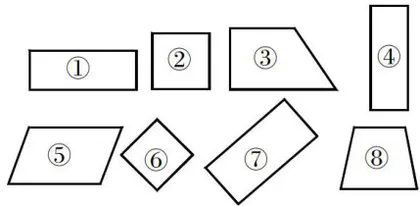
师：同学们，我们把长方形的长边叫“长”，短边叫“宽”；正方形的四条边都是“边长”。图1中哪些图形是长方形？哪些是正方形？哪些是平行四边形？

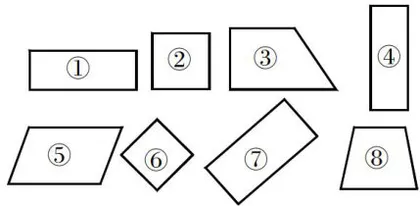
生1：长方形是 ①④⑦ ，正方形是 ②⑥ ，平行四边形是 ⑤ 。

师：都说对了。接下来我们来看看这个长方形的长是多少，宽是多少？

生2：长是14厘米，宽是10厘米。

师：老师让这个长方形动起来，现在这个长方形的长和宽分别是多少？

生3：长是12厘米，宽是10厘米。

师：你们有办法让这个长方形继续运动，变成正方形吗？

生4：长减少2厘米，这样正方形的边长都是10厘米了。

师：现在这个图形既是长方形，又是正方形，所以我们说正方形是特殊的长方形。老师这里有三个椭圆，你们能用这三个椭圆表示四边形、长方形和正方形的关系吗？

生5：四边形最大，长方形次之，正方形最小。

师：同学们，我们知道了四边形、长方形和正方形之间的关系。如图2所示，信封里装的是一个四边形，猜一猜不可能是什么形状？

生6：不可能是三角形，因为三角形不是四边形；也不可能是平行四边形，因为我们看到了两个直角。

师：猜一猜可能是什么形状。

生7：长方形、正方形或者直角梯形。（教师出示这个图形后发现是直角梯形）

在这个教学片段中，教师设计了三个拓展练习题，以促进学生建立长方形和正方形的表象。第一个练习题是让学生利用边和角等元素判断平行四边形、长方形和正方形，这不仅有利于学生进一步感知长方形和正方形的特点，而且有助于他们通过比较掌握正方形和长方形之间的联系与区别；第二个练习题是让学生在动态运动中感受长方形与正方形之间的变化，为用集合图表示四边形、长方形与正方形的关系积累了丰富的活动经验；第三个练习题是让学生观察部分图形，猜测信封里藏着的图形的形状，帮助他们形成合理的认知结构。

总之，教师要引导学生经历观察、操作、测量和比较等活动过程，让学生在充分感知的基础上，利用自主探究和小组合作发现长方形和正方形的基本特征；借助多种感官协调参与动手操作活动，让学生验证和应用长方形和正方形的基本特征。整节数学课中既有静悄悄的思考时间和空间，又有热热闹闹的动手和讨论活动，两者交织在一起如同一首交响曲。教师引导学生在刨根问底中将眼见为实转化为理性验证，让学生学会用定性描述和定量刻画相结合的方式认识长方形和正方形。