学生解决“排队问题"的能力分析
作者: 蒯吉一、问题的提出
“排队问题"是指学生把排队中的实际问题转化为数学问题,要求学生在理解问题的基础上用画图的策略去解决。为了了解学生关于“排队问题"的学情,笔者设计了前测题。通过对前测结果的分析,为教学设计提供依据,更好地优化学生在解决问题中的策略的选择。
二、研究目的及主要问题
1.研究目的
分析学生对“排队问题"的求解能力和策略选择,为小学数学教学提供参考依据。
2.研究的主要问题
(1)一年级的学生能否自觉想到用画图的策略解决“排队问题”;
(2)一年级的学生能否正确建立文字与符号之间的联系;
(3)一年级的学生解决“排队问题"时表示方式的选择,如具体图、文字、符号等。
三、研究设计
1.研究对象
一年级6个班共216名学生,均未接触过这类题目。
2.测试和访谈题目
本次测试采用笔试方式(如图1),教师先出示纯文字的“排队问题”,考查学生是否会想到画图的策略;再出示不完整图,考查学生能否正确建立文字与符号之间的联系,以及采用何种画图方式。
3.测试和访谈过程
在测试时,考虑到一年级学生识字少,教师进行了读题,让学生先完成前测练习1,再完成前测练习2。学生在解题过程中,没有任何的讨论与交流,测试时间统一安排为20分钟。整个测试过程基本反映了学生在自然状态下独立解答这一问题的水平。测试后,教师对学生的解题情况进行初步整理,选择了部分学生进行访谈。

四、“排队问题”的测试结果分析
1.一年级几乎没有学生想到用画图的策略解决“排队问题”
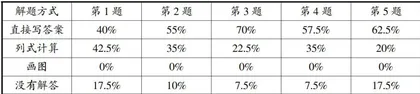
从表1可以看出:学生在完成前测练习1的“排队问题"时,没有学生想到用画图的策略来解决,大多数学生采用直接写答案或列式计算来解决; 10% 左右的学生不能独立解答这类题目,可见“排队问题"对一年级学生来说比较困难,主要原因是无法选择合适的解题策略和不理解题目的意思。
2.学生在选择画图方式时倾向于用符号来表示,并且在解题过程中实现了画图的迁移
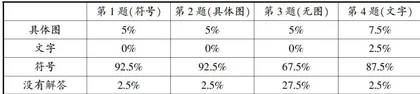
从表2可知,学生在完成前测练习2的“排队问题"时,由于题目中有具体图、文字及符号等,所以多数学生采用多种方式来解决这些问题。当然,学生选择画图的方式与题目给予的半成品图有关,比如第1题是用符号出示的,有 92.5% 的学生选择用符号来画图;第2题虽然是用实物图出示的,但是学生受第1题的影响,仍有 92.5% 的学生选择用符号来画图;第3题是用文字出示的, 67.5% 的学生受到符号画图的正迁移,有 27.5% 的学生还不能选择合适的画图方式来解决;第4题是用文字出示的,受到题目中文字的负迁移,有 2.5% 的学生选择用文字来表示。
而且,面对实物图、文字或符号等表示方式,学生几乎都选择用符号来表示题目的意思。尤其是第3题,题目没有提供任何画图方式,仍有67.5% 的学生选择用符号来解决这道题目,可见大部分学生已经能够选择画图的方式。
3.部分学生在解决“排队问题”时不能正确建立文字与符号之间的联系
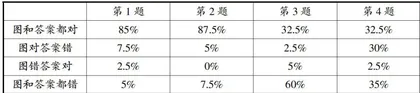
由表3可以看出一年级的学生在解决“排队问题"第1题和第2题(求一共有多少人或动物)时,约 90% 的学生已经能够把题目中的文字转化为符号图, 85% 左右的学生能够正确找出图中一共有多少人或动物。解决第3题(求一共有多少人)时,32.5% 的学生能够正确建立文字与符号之间的联系,但是有 60% 学生不能独立建立文字与符号之间的联系。解决第4题(求谁和谁之间有几人)时,约 60% 的学生能够建立文字与符号之间的联系,但是 30% 左右的学生不能正确找出图中表示谁和谁之间的部分。
4.学生在同一题中出现了不同的符号图,写出了不同的算式
在学生上交的答卷和访谈记录中,笔者发现学生面对同一道题目虽然都选择用符号来画图,但是他们画出了不同的图,写出了不同的算式。
类型一:所有人的表示都一样(如图1所示)。

本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:sxjz20250330.pd原版全文
图1
类型二:突出了“小丽"和“小强”这两个人。
用符号强化: 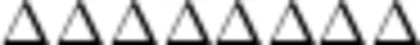 Δ △△或
Δ △△或 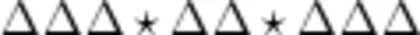 。
。
用文字强化: ΔΔΔ 小丽 ΔΔ 小强△△△。
用符号和文字强化:  $\blacktriangle$ △△ 1 ΔΔΔ 。 小丽小强
$\blacktriangle$ △△ 1 ΔΔΔ 。 小丽小强
面对同样的符号图,题中都突出了“小丽"和“小强"两个人,学生却写出了不一样的算式: 3+1+2+1+3=10 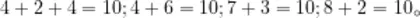
更加可喜的是,有一名学生想到用两种方法来解决这道题目。
方法一:  小丽 ΔΔ 小强 Δ △△ $\cdot,4+2+4=10。$ (204号
小丽 ΔΔ 小强 Δ △△ $\cdot,4+2+4=10。$ (204号
方法二:小丽 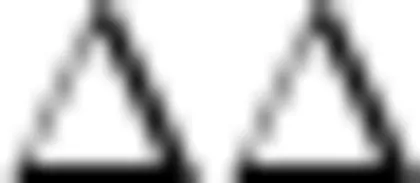 小强, 2+2=4,3+ 4+3=10 。
小强, 2+2=4,3+ 4+3=10 。
五、结论
1.从测试和分析中得出的结论
(1)大部分学生已经具备画图策略的迁移能力。
(2)虽然学生在选择画图方式时倾向于用符号来表示,但与题目出示的形式有关。
(3)学生解决“排队问题"的能力具有差异性:有的学生能根据符号图写出不同的算式,有的学生不能正确建立文字与符号之间的联系。
2.对小学数学教学的启示
(1)在教学中教师要注重培养学生的画图能力,渗透符号化思想
(2)教师要唤醒学生已有的经验,引导学生更快进入新授知识的学习。
(3)教师要承认学生之间的差异,尊重学生的个性,促进学生的发展。
(4)教师必须了解学情,因材施教。
本文为全文原貌 未安装PDF浏览器用户请先下载安装
原版页码:sxjz20250330.pd原版全文