用几何直观建设有质量的深度学习

随着新课程理念的不断深化，数学教学不再是单纯地传授数学知识，教师应重视学生思维能力和综合素养的培养。几何直观就是学生通过图形助力数学思考，从根本上来说就是借助数形结合的思想探寻问题解决的策略。在数学教学中，教师从数学学科特质出发，适切运用几何直观对学生进行积极引导，让学生以几何直观为原型，以动作思维为支撑，以动手操作为纽带，建设有质量的深度学习。

一、以“形”寻“策”

思考是学生解题策略形成的根基，思考越深人，则策略愈有质量。低年级的学生还处于前运用阶段，大多以形象思维为主，他们常常在解决一些复杂问题时，难以厘清其中复杂的数量关系，无法探寻到解题的入口，无法明晰解题的关键所在。要渗透解题的策略，教师就要在教学中巧妙运用几何直观的策略。通过图形的助力，学生往往能逐步厘清数学关系，从而探寻解决问题的策略。反之，如果没有图形的助力，教师只是把解题思路抛给学生，常常会让学生陷入糟糕的解题境地。因此，在教学的过程中，教师要善于运用几何直观，以形助数，让图形成为学生解题策略形成的有力支撑。

案例1以题组教学为例

（1）二（1）班有男生17人，女生比男生多9人，女生有几人？

（2）二（1）班有男生17人，比女生多9人，女生有几人？

师：请大家先独立思考，并完成以上题组。（大部分学生感到困惑，一筹莫展）师：其实画线段图的方法可以很好地帮助我们解决本题，大家可以试一试。（学生立刻开展探索，但很快遇到了问题）

生1：可我不会画第（2）题中的女生人数。

师：这里有“比女生多9人”，那是男生多还是女生多？

生1：男生多。

师：谁应该分为两个部分呢？多的9人应该是哪个部分呢？

生1：我明白了。（学生作图，教师巡视后展示图1所示的线段图）

师：下面我们一起来观察图1，第（1）题可以知道什么？

生2：女生人数多，就把女生人数分成了两个部分，即与男生一样多的和比男生多的，再将两个部分相加即为所求的女生人数，这里选择用加法计算。

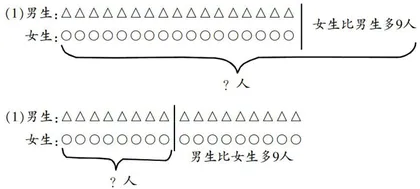
师：分析得非常好，谁来说一说第（2）题？

生3：这里“男生比女生多9人”就是男生人数多，把男生人数分成了两个部分，用男生人数减去男生比女生多的部分，剩余的就是男女生同样多的部分，也就是女生人数，这里选择用减法计算。

思考是解题策略形成的重要前提，思考得准确，才能让解题策略快速落地。在解决这一题组之前，学生的解题经验不够丰富，还未形成画图的习惯。在这里，教师鼓励学生用“形”寻“策”，让思考产生效果，学生在作图之后，真正意义上理解了“比多少"问题中的数量关系，达到了厘清数量关系、打通思维障碍、获得解题策略的目的。

二、以“形”探“理”

高质量的数学学习并非靠学生熟练记忆和反复练习即可，而应淡化机械的背与记，强化学生对知识本质的理解，通过数学探究达到“知其然且知其所以然"的目的。要让学生明晰数学本质，教师要巧妙利用几何直观的策略，化隐性为显性，让学生通过探究明晰隐藏于数学定理、规律和概念背后的数学道理，获得对数学知识的深度理解，提高思维能力。在学生探寻数学道理的过程中，教师要以图形适当点拨引导，帮助学生找到思考的增长点，从而在深度学习中发展其思维。

案例2 倍的认识

活动1：秋天到了，兔妈妈家的萝卜园又丰收了，兔妈妈带着兔宝宝们一起去拔萝卜。请大家仔细观察情境图，你们发现了什么？（教师出示情境图后，学生发现白萝卜有2根，胡萝卜有6根，红萝卜有10根）

活动2：如果把2根白萝卜看成1份，那胡萝卜的根数可以用几个几表示？你们能说出白萝卜和胡萝卜之间的倍数关系吗？再借助手中的学具摆一摆。（教师再次呈现图片，让学生充分感知胡萝卜的根数有3份白萝卜那么多，在学具的助力下得出“胡萝卜是白萝卜的3倍"的结论）

活动3：让学生借助手中的学具去摆一摆和圈一圈，试着探究白萝卜和红萝卜之间的倍数关系。（学生在操作后很快得出了结果）

活动4：事实上，这样的倍数问题在生活中随处可见，请大家利用圆片摆出一组倍数关系。（学生在操作后集体交流）

活动5：如图2所示，第二行该怎么摆，则可以看出是第一行的4倍？

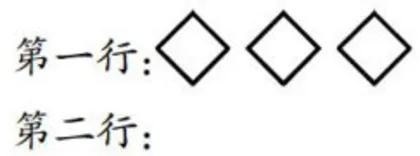
学习“倍数的认识"时，数形结合的思想有着广泛的应用性。在上述教学片段中，如果教师只是将知识传输给学生，那么学生的思考仅停留在表层，对于倍数的概念缺乏切实的体会和感悟。学生在探索中结合图形直观开展阐述，并结合具体实物量的比较从而抽象得出“倍”，最终能在追根溯源中深刻理解数学本质。学生以图形探寻道理可以让模糊的思考更深入、更清晰，让深度学习更有质量。

三、以“形”明“律”

数与形有着天然的、密不可分的联系，一些复杂数学问题往往兼具数与形的特征。对于抽象思维欠缺的小学生而言，如果教师将规律直接呈现出来，学生则会因缺乏“形"的支撑而无法真正理解。如果教师巧妙运用数形结合，引导学生经历化抽象为具体的过程，引导学生更加直观地发现数学规律，归纳概括数学规律，则可以发展学生的抽象推理能力，让数学课堂在深度学习中焕发生命活力。

案例3数与形

问题1：计算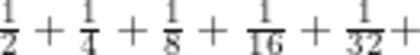

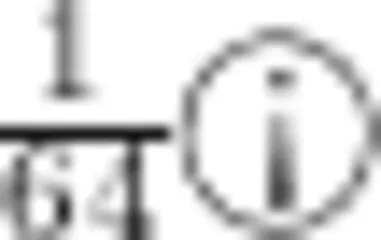
师：请大家在独立思考后试着计算。（学生思考片刻后开始计算，教师在巡视过程中发现所有学生通过通分进行计算）

师：大家都能计算得出结果，非常好！问题2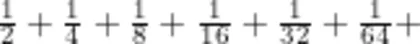

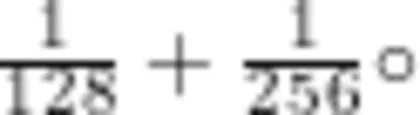（学生观察问题后陷入困境，苦思无果）

师（点拨）：其实我们可以转变思考的方向，试着画图来解决这个问题，例如在一个图形中分别标一标

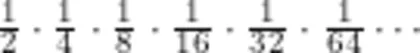（学生立刻有了方向，得出了图3所示的几种画法）

师：下面我们开展小组合作学习，一起来分析图3，说一说你们发现了什么？

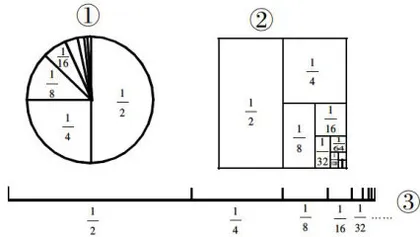
生1：从 开始，之后的每个数都是前一个数的 就这样一直加下去，它的和与1越来越接近，最后会等于1，所以只需用1减去最后一个加数的差，就能计算出结果。

在教学的过程中，教师巧妙地引导学生画图观察。学生亲历画图、观察、计算、推理的过程，从而让复杂计算中的规律形象化、简约化，切实感受数形结合的巧妙应用，促进思维的深度发展。

几何直观不仅是教师数学教学的价值取向之一，也是学生数学学习的重要方法。教师巧妙运用几何直观的策略，以“形”寻“策”以“形”探“理”以“形"明“律”，能推动学生的数学学习不断走向深入，最终实现深度学习。