数学文化在中考数学试题中的呈现及思考

引用格式 金杨建，数学文化在中考数学试题中的呈现及思考.教学与管理，2025（13）：66-71.

《义务教育数学课程标准（2022年版）》在课程理念中指出：课程内容的选择应关注数学文化，继承和弘扬中华优秀传统文化；在课程实施中强调学业水平考试中试题命制应创设合理情境，根据考查意图，结合学生认知水平和生活经验，设计合理的情境，并关注情境的真实性，适当引入数学文化。数学文化在数学教育中的价值、意义和重要性已获得广泛认同，各地中考数学卷中渗透数学文化的试题也大量出现。对这类试题的研究不仅可以窥探数学文化题命制的思路与理念，也可以补充课堂教学中数学文化渗透的素材与方法。

一、数学文化题的意涵

数学在人们认识世界和改造世界的过程中发挥了重要作用，人们对数学的认识也在不断完善和发展，数学是人类文化的一个重要组成部分。美国数学家怀尔德（R.Wilder）认为数学文化的发展已经达到了一个较高的水平，并最早系统提出了“数学——作为一种文化体系”的数学哲学观。李大潜院士对"数学是什么"进行了归纳：数学不仅是一类知识、一种科学的语言、一个有力的工具；数学也是各门科学的基础，是一门重要的科学，是一种关键性的、可实现的技术；同时，数学更是一种先进的文化，是人类文明的重要基础[2]。

数学文化是国际数学教育研究最为关注的热点之一。然而数学文化的内涵目前尚未形成统一的认识，概括起来主要有五个角度的理解：数学学科的角度；文化的角度；数学共同体的角度；数学活动的角度；系统的角度。南开大学顾沛教授从文化的角度给出了数学文化的内涵，他认为，狭义的“数学文化”是指数学的思想、精神、方法、观点、语言，以及它们的形成和发展；广义的“数学文化"除上述内涵以外，还包含数学史、数学家、数学美、数学教育、数学与人文的交叉、数学与各种文化的关系，等等4，这也是目前主流的观点。《普通高中数学课程标准（2017年版）》中给出的数学文化的含义，包括了上述狭义观点；还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动。本文对数学文化的理解，采用顾沛教授认为的广义内涵。基于以上分析，笔者认为数学文化题简言之就是显性或隐性融入数学文化的试题。关于数学文化的价值，学者们虽然研究角度不一，但区别较少。归纳整理发现，数学文化的价值主要体现在：德育价值；美育价值；思维训练的价值间。因此，数学文化题也具有上述三个方面的价值。

二、数学文化在中考数学试题中呈现的类型

数学文化题的分类目前尚无统一标准。如根据试题编拟中数学文化元素的取材来源将数学文化题分为“源自数学名题”和“源自文化事物"两类；根据试题中数学文化元素的背景将数学文化题分为“以中国数学典籍史料中优秀成果为背景”，“以外国数学家创造的数学名题为背景”和“以数学与其它学科的联系为背景”三类；根据试题中数学文化的考察角度将数学文化题分为"渗透中国古代数学史考察”，“渗透数学精神”和“渗透数学应用”三类；根据命题素材载体和价值指向角度将数学文化题分为“以数学文化为载体的数学名题（命题渗透数学史、命题渗透数学美、命题渗透理性精神）”和"彰显数学文化的数学应用题（关注社会热点问题、突出数学建模意识）两大类五小类；根据试题中数学文化内容类型将数学文化题分为“数学史”“数学与生活”“数学与科学技术”和“数学与人文艺术"四类；根据试题中数学文化的特征和教育价值将数学文化题分为“以古代名著为蓝本、弘扬数学文化历史”“以生产生活为载体、渗透数学应用文化""以数学游戏为背景、激发数学探究兴趣”"以经典名题为原型、拓展数学思维深度”和“以数学活动为抓手、感悟数学理性精神"五类[2，等等。笔者抽取了2024年82份中考数学试卷中涉及的数学文化题进行分析，根据数学文化元素在试题中所产生的作用和呈现方式对数学文化题进行分类。

1.作为引入素材点缀式呈现

2019年11月，教育部发布的《关于加强初中学业水平考试命题工作的意见》中指出，拓宽试题材料选择范围，丰富材料类型，增强情境创设的真实性、典型性和适切性，提高试题情境设计水平[13]。中考试题的命制不仅要体现知识立意，也要体现能力立意，更要指向素养发展立意。单纯对知识考察的试题略显单薄，同时对学生素养的提升也略显欠缺。数学文化素材是试题情境呈现的一个重要载体，是发展学生数学素养的一个有效途径。试题中显性的介绍有关数学文化的素材，如数学成果、数学名著、数学名人、数学图片等，在传递文化价值的同时，对试题的引入起到一定的辅助作用，使试题主体内容的出现显得不突元，有助于丰富试题的情境。

2024年云南卷第1题：中国是最早使用正负数表示具有相反意义的量的国家．若向北运动100米记作 +100 米，则向南运动100米可记作_____。

2024年安徽卷第12题：我国古代数学家张衡将圆周率取值为 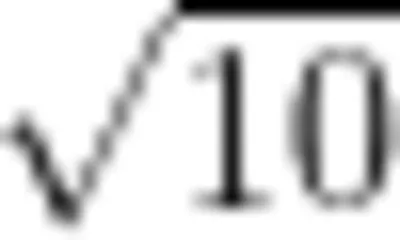，祖冲之给出圆周率的一种分数形式的近似值为 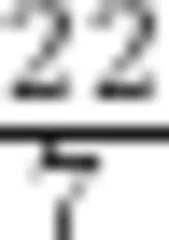。比较大小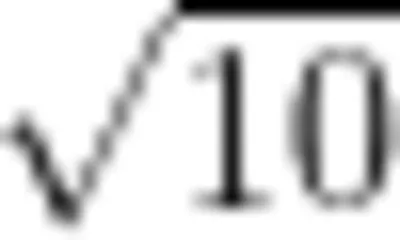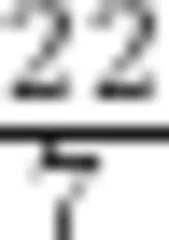：  -（填“ > ”或“ < ”）。

负数的引入、圆周率的近似值是古代中国在数学上取得的两个显著成就。用正负数表示具有相反意义的量，是正负数知识的内涵。中国作为最早引人负数概念的国家，在数学发展史中起到举足轻重的作用。古代中国数学家在计算圆周率中也取得重要的成就：张衡将圆周率取值为 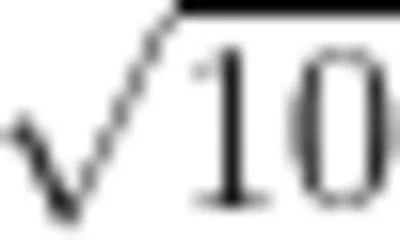、祖冲之给出圆周率的分数近似值 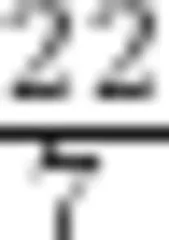都领先于同时代的西方。这些数学文化元素是试题的点缀成分，对学生而言没有任何解题信息价值（上述两题中，如果去掉含有数学文化的文字，依然是一道完整的试题），但是学生在阅读试题的过程中，能够了解中国或中国数学家在数学中取得的重要成就，无形中能提升学生的民族自豪感，增强文化自信，同时也使得考察内容的呈现不显得过于突兀。因此，教师平时在教学中，也可以在合适的时机有意识的渗透这类数学文化信息，这有利于增长学生的数学文化素养，提升学生数学学习的兴趣和自信心。

2.作为试题来源复制式呈现

科学性是试题命制的前提和生命线。就数学文化题而言，其文化源头必须准确真实，数据信息必须正确科学。文化性又是数学文化题一个显著特征，因此数学文化题不仅要确保试题的科学性，又要体现其文化性（展现数学知识、方法和思想的历史、应用和发展过程），以此传承数学文化、发展学生数学核心素养。古代中国出现了大量的数学名著，如《周算经》《九章算术》《孙子算经》《增删算法统宗》等，其中有大量的数学名题，这些试题的科学性已经历了历史的检验，其文化性母庸置疑。中考试题直接选取这些数学典籍中的数学问题，一方面素材来源真实、传承有序，另一方面又为古代名题赋予新的使命。这不失为命制数学文化题的一个有效方式。

2024年天津卷第9题：《孙子算经》是我国古代著名的数学典籍，其中有一道题：“今有木，不知长短。引绳度之，余绳四尺五寸；屈绳度之，不足一尺。木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，问木长多少尺？设木长 x 尺，绳子长y尺，则可以列出的方程组为_____。

2024年烟台卷第9题：《周算经》是中国现存最早的数理天文著作，书中记载这样一道题：“今有女子不善织，日减功迟，初日织五尺，末日织一尺，今三十日织讫，问织几何。”意思是：现有一个不擅长织布的女子，织布的速度越来越慢，并且每天减少的数量相同，第一天织了五尺布，最后一天仅织了一尺布，30天完工，请问她一共织了多少布。

中国古代经典数学著作中的问题，往往以文言文的形式呈现，命题者需要对其进行翻译或注解，这样才能帮助解题人更好地理解题意，减少审题障碍，真正起到对数学能力的考察。学生在阅读名题原文时，能感受到古代语言的魅力，在用所学知识解决古代数学问题时，又能亲身感受古代数学问题的经典，体会数学知识的传承与进步，仿佛在与古人对话。值得注意的是，这类试题若仅呈现原文，则生涩难懂、学生理解可能有障碍；若仅出现译文，则平铺直叙、缺少古代名题的韵味；若既呈现原文又给出译文，则行文略显繁琐，但这却是目前数学文化题命题的主流选择。因此，教师平时应更多的关注数学经典著作（中国的和国外的）中的问题，选取适切的问题在教学中适时呈现，或作为例题、或作为练习题、亦或作为教学情境，这不失为一个丰富教学素材、拓宽学生视野的方法。

3.作为解题信息应用式呈现

中考是学生接受九年制义务教育中一次重要的考试，势必具备一定的选拔功能。因此中考试卷中出现的数学文化题不仅要关注对基础知识、基本技能的考察，也要适当突出对基本思想、基本活动经验的考察，从而承担一定的选拔功能。数学的发展历史中出现过许多有趣而又深刻的发现，这些发现推动了数学的发展。中考试题中借助这些成果，作为解题的重要信息，既能体现数学的发现美和应用美，又能增强对学生数学综合素养的考查，还能提升学生对数学的好奇心，未尝不是一个很好的选择。不过值得提醒的是，数学文化试题作为中考考题应兼具公平性，数学文化元素所提供的解题信息对于不同的学生而言应该是公平的。

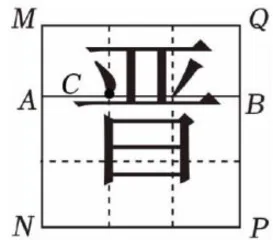
2024年山西卷第12题：黄金分割是汉字结构最基本的规律。借助正方形习字格书写的汉字“晋”端庄稳重、舒展美观（如图1）。已知一条分割线的端点A，B分别在习字格的边MN，PQ上，且AB/NP，“晋”字的笔画“、”的位置在AB的黄金分割点C处，且 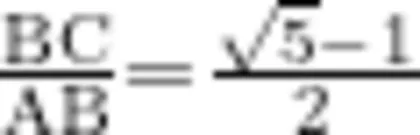若 NP=2cm ，则 BC的长为 cm （结果保留根号）。

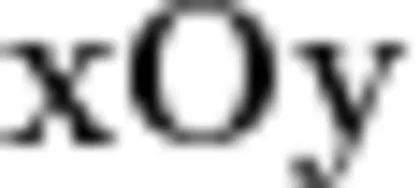2024年枣庄卷第16题：任取一个正整数，若是奇数，就将该数乘3再加上1；若是偶数，就将该数除以2。反复进行上述两种运算，经过有限次运算后，必进入循环圈 ，这就是“冰電猜想”。在平面直角坐标系 中，将点 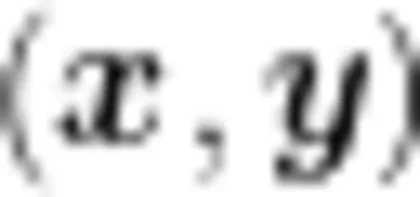中的 x，y 分别按照“冰電猜想”同步进行运算得到新的点的横、纵坐标，其中 x，y 均为正整数．例如，点（6，3）经过第1次运算得到点（3，10），经过第2次运算得到点（10，5），以此类推。则点（1，4）经过2024次运算后得到点 O

黄金分割是初中数学学习中的一个重要知识，对所有学生而言是公平的；同时，试题中又给出了√5-1这一重要信息，对考生而言又是友善的。冰猜想（即角谷猜想）在教材中虽未出现，但试题中将其内容完整的呈现，能够考察学生阅读理解能力、学习能力和思维能力；将冰電猜想运用到平面直角坐标系中点的横、纵坐标对学生而言又有一定的创新性，这些对所有学生而言也是公平的。另外，这两道试题又能充分展现数学美，这是数学文化题的另一个显著特征。黄金分割中体现的美众所周知，能直观感受，特别是试题中出现正方形习字格书写的汉字“晋"字，能让人眼前一亮。然而冰猜想这类问题中则隐藏着数学“冷而严肃的美”，其中蕴含着数学知识中的结构之美、数学推理中的思维之美。这正体现了顾沛教授说的，“数学的美，在于数学思想深刻之美”。因此，教学中可以适当增加一些具有熟悉或陌生数学文化背景的问题，让学生感受数学的发现和应用的之妙，从而提升学生的思维能力。