基于学习进阶的中学物理教学设计

中图分类号：G633.7 文献标识码：A文章编号：1003-6148（2025）4-0040-8

单摆作为简谐运动的典型实例，与日常生活、生产实践、科学研究有着密切联系[，具有较高的教学价值。根据课程标准要求，本节需要解决三个问题，即“单摆”模型的建构、“简谐运动”的证明以及单摆周期影响因素的定性探究与定量分析。本研究以学习进阶理论为指导，进行了学情分析、学习过程设计，旨在实现概念理解与思维能力的进阶，促进学生核心素养的逐步提升。

1基于学习进阶的教学设计模型

物理学科核心素养从物理观念、科学思维、科学探究、科学态度与责任四个维度提炼出基于学科本质的育人价值，明确了学生应达成的必备品格、关键能力和正确价值观，从而有效落实立德树人的根本任务。学习进阶是对学生的思维由简单到复杂、由浅入深的层级刻画，在课程、教学与评价领域均已得到广泛应用[2]。基于对物理学科核心概念和关键能力的学习进阶进行了理论研讨和实证研究，本文建构了学习进阶的教学设计模型，如图1所示[3]。

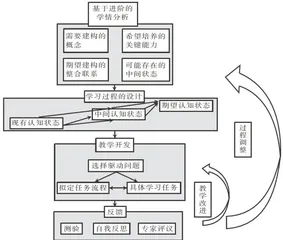
2 基于学习进阶的“单摆”教学设计

本文以学习进阶教学设计模型为指导，结合学生“机械振动"所学情况进行了基于学习进阶的学情分析，并基于核心素养视域制订了本节教学目标。在教学过程中，建立了“单摆"概念理解的发展层级模型，结合现有认知状态和中间状态合理设计了“简谐运动”的证明和单摆周期影响因素的探究实验，促进学生达到期望认知的状态。

2.1 基于学习进阶的学情分析

基于学习进阶理论，从概念建构、关键能力培养、建构整合联系、设想中间状态四个维度，分析学生学情，并作为后续教学过程的合理指导。

2.1.1 需要建构的概念

基于知识学习的由浅入深，综合考虑学生现有认知水平，制订如表1所示的发展层级模型

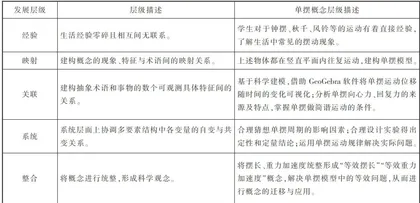
2.1.2 希望培养的关键能力

单摆作为受力与运动情况均较为复杂的简谐运动实例，其所涉及的分析论证方法蕴含着极丰富的教育价值[4，学生通过学习能促进对简谐运动一般规律的理解与应用，从而丰富运动与相互作用观。学生通过对生活中摆动现象的分析，甄别摆动现象中的主次因素，建立单摆模型，培养科学建模能力。在单摆的动力学证明中，渗透小角度的近似处理方法，培养学生利用极限思维和近似法的科学论证能力。在运动学证明中，结合GeoGebra软件培养学生数据采集和信息技术应用能力，进一步提升科学探究能力。在探究单摆周期与摆长的定量关系实验中，结合手机Phyphox软件，先用控制变量法定性探究出单摆周期与摆长有关，再用图像法处理数据得出定量结论。学生通过物理学史，体悟科学道路的艰辛，培养实事求是的科学态度，树立正确的价值观，在学习进阶中提升学科核心素养。

2.1.3 期望建构的整合联系

单摆的受力和运动情况均较为复杂，整合了简谐运动的振动图像及回复力的特点，圆周运动的向心力特点与能量转化等知识，蕴含着极丰富的运动与相互作用观念、能量观念的培养价值[5]。基于前面所学关于简谐运动的描述，从简谐运动的回复力和能量出发，引导学生尝试从两个维度证明单摆的运动为简谐运动，有效培养学生运用所学解决实际问题的能力。学生基于周期与摆长的定量关系，理解利用单摆测量重力加速度的原理，体会该公式的妙用。

2.1.4 可能存在的中间状态

学生有较强的好奇心和求知欲，若教师将传统实验与信息技术融合，能够激发学生的学习兴趣，营造积极主动的课堂学习氛围。学生已经掌握了从运动学和动力学两个角度证明物体是否做简谐运动。但还存在以下问题：由于单摆运动的特点，学生很难联想到其图像为正弦函数曲线；对回复力的来源不明确，且对小角度下的近似处理方法不够熟悉；根据已有器材，学生能够利用控制变量法设计实验，定性地分析出单摆周期与摆长有关，与质量、摆角无关的结论，但由于数据处理能力的不足，较难得出单摆周期与摆长的定量关系。

2.2 基于学习进阶的学习过程设计

基于学情分析，教学过程从教学目自标的制订、“单摆"模型建构、“简谐运动"证明、单摆周期影响因素的定性与定量研究四个维度展开。各个维

度都注重基于学生的已有经验进行设计，从而促进学生的学习进阶。

2.2.1 教学目标

教学目标是教学过程实施的总纲领，基于学习进阶的学情分析，制订本节教学目标，如表2所示。

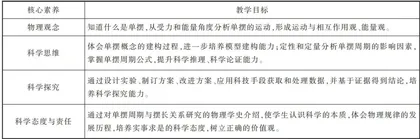
2.2.2 单摆模型建构

学生现有认知状态：对生活中的摆动现象有直接经验。

课题引人：以蛇摆视频作为引人。学生观察到蛇摆的运动时而井然有序，时而杂乱无章，从一开始的“一"字排列，经过一段时间后，在某个瞬间又恢复成“一"字排列。

设计意图：激发学生的学习兴趣和探究欲望，并为后续引导学生探究单摆周期影响因素与揭秘蛇摆运动作铺垫。

教师：荡起的秋千、运动的钟摆、摇曳的风铃等都是司空见惯的现象。它们都在某一位置附近做往复运动。思考以下几种情境，哪些最贴近上述物体的运动？（图2）

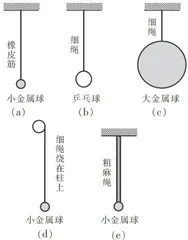
学生：均不贴近。图2（a）和（d）摆动过程中摆长会发生变化；图2（b）空气阻力对物体运动的影响不可忽略；图2（c）球的直径与细绳相比不可忽略；图2（e）绳子的质量与物体相比不可忽略。

教师：至此，引入一个物理模型，如图3所示，由细线和小球组成一个单摆，其中细线的质量可以忽略；小球的直径与细线的长度相比可以忽略；摆动过程中细线的形变量可以忽略；小球摆动过程中空气阻力可以忽略。因此，单摆是一种理想化模型。

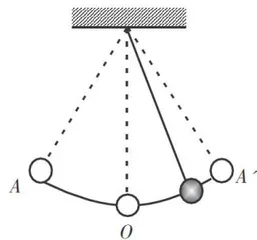
设计意图：大多教师直接给出单摆模型，缺乏符合学生认知规律的铺垫，学生起初难以信服，且这种灌输式教学与新课标的素养导向不相匹配。通过上述5幅图，简单演示一下摆球的运动，结合蛇摆、秋千等摆动，培养学生忽略次要因素、关注主要因素的科学思维，体会单摆模型的建构过程，加深对单摆模型的认识。此环节通过呈现现象、观察体会、归纳总结，学生完成了从经验到映射层级的发展。

2.2.3 “简谐运动”的证明

教师：单摆能看作简谐运动吗？有什么方法可以证明？

学生：可以从运动学角度和动力学角度证明。如果单摆的回复力满足 F = - k x 或位移一时间图像是一条正弦曲线，即可得证。

教师：小组讨论一下摆球的平衡位置在何处？为什么摆球能在以平衡位置为中点的一小段圆弧上做往复运动？单摆回复力的来源是什么？

学生：平衡位置在 o 点；回复力的来源是摆球所受合力：摆球重力沿圆弧切线方向的分力。

教师：有小组得出回复力的来源是摆球所受的合力。结合摆球最低点即平衡位置回复力为0的特点，很显然最低点摆球所受合力不为0，合力提供了向心力，与平衡位置回复力为0矛盾。

设计意图：通过小组讨论的方式，交换想法，进行思维碰撞。摆球合力提供回复力是学生容易陷入的误区，对于此看法，不急于否定，而是引导学生根据所学理性分析，一步步走出误区。

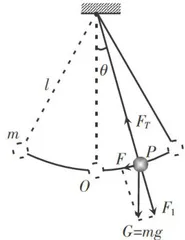
教师：如图4所示，摆球在运动中受到细线拉力和重力的作用。细线的拉力和重力沿径向分力的合力提供向心力；重力沿圆弧切线方向的分力使小球向平衡位置运动，提供回复力，即 F = -mgsin0（“-"代表回复力方向与位移方向相反，即指向平衡位置）。很显然，该表达式不符合简谐运动回复力的特征。如果单摆做小角度摆动（图5），情况如何呢？请结合表3中所给数据，小组讨论进行证明。

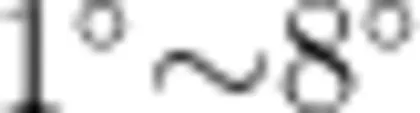
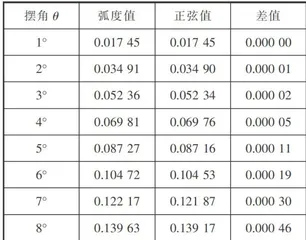
学生：在摆角很小的情况下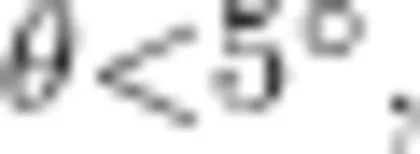（ ，摆球运动的圆弧可以看成直线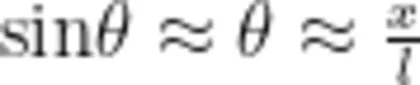， ，即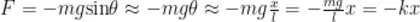 定的单摆，质量与摆长不变，可视为定值。所以，摆角 的单摆运动可视为简谐运动。

设计意图：通过分析单摆回复力和向心力的来源，培养学生运动与相互作用观；通过证明单摆小角度摆动是简谐运动，培养极限法的科学思维。

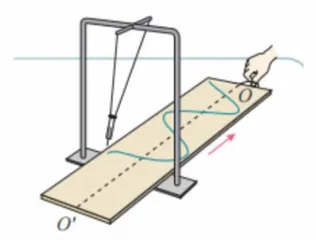
教师：我们从动力学角度，证明了单摆做小角度摆动时可以视为简谐运动，其位移一时间图像应该是一条正弦曲线。但是，我们观察到的单摆运动是一个竖直平面内的圆周运动，似乎与正弦曲线毫无联系。思考：图6所示实验过程中的图像是否完美？是否与正弦曲线一致？