借助Mathematica数学软件探究椭圆摆微振动问题内涵

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2025）4-0052-6

当前，在国家“双新"教育改革的背景下，如何应对“综合性大和变式后难度明显陡增"这一情况成为了中学教师和学生亟需面对的一个问题[1。大多数高考试题都具有丰富的内涵，而内涵的隐蔽性使之通常可能存在于一个全新的情境当中，也可能存在于一个轻描淡写的题设当中（如一些近似条件的设置），需要做题者进行一般性情况下的探究。与此同时，这些内涵的抽象复杂性和物理图景通常难以通过纸笔计算所明晰，而Mathematica这款数学软件的存在便能在很大程度上解决这一问题。下面以2024年6月浙江省物理选考第9题为例进行分析说明，探究其背后的椭圆摆微振动问题内涵，同时运用Mathematica数学软件展现此内涵的清晰物理图景。

1 原题呈现

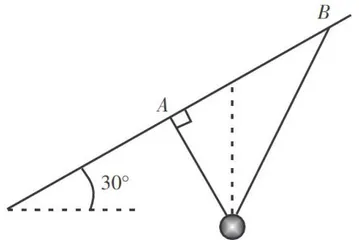
例题如图1所示，不可伸长的光滑细线穿过质量为 0 . 1 k g 的小铁球，两端 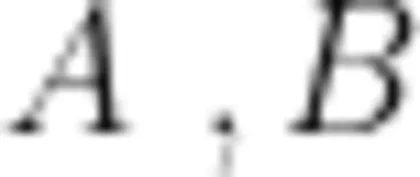悬挂在倾角为 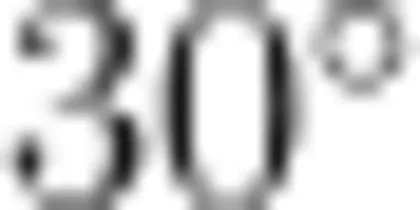的固定斜杆上，间距为 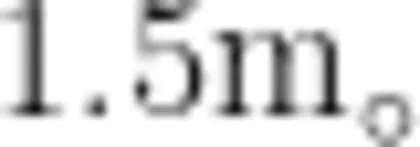小球平衡时，A端细线与杆垂直；当小球受到垂直纸面方向的扰动做微小摆动时，等效于悬挂点位于小球重垂线与 A B 交点的单摆，重力加速度 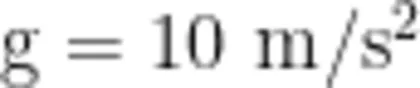，则（ ）

A.摆角变小，周期变大

B.小球摆动周期约为2s

C.小球平衡时，A端拉力为√3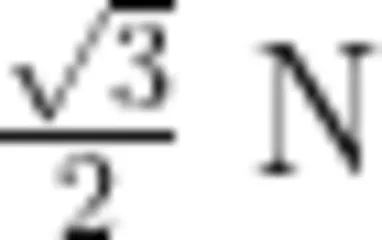

D.小球平衡时，A端拉力小于 B 端拉力

2 题设中易被忽略的条件

本道高考题以细线穿球悬挂（“滑轮"模型）等效成单摆模型的新颖情境，考查学生对共点力平衡的计算和单摆做简谐运动时周期公式的综合运用情况。细线穿球悬挂的复杂情境中，运用小球处于共点力平衡，求出绳长与相关角度的关系，属于规律的运用，是物理观念水平4；小球在微小扰动下可等效成单摆模型，求出相应摆长，考查学生建立模型解决实际问题的能力，属于物理思维水平 。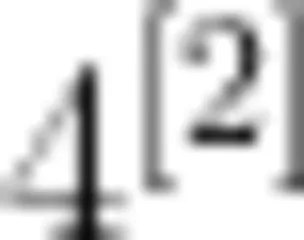

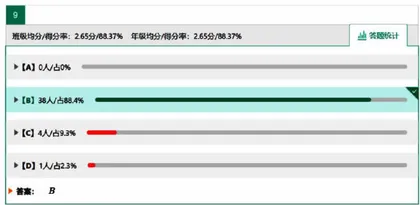
注意到上述题于中，命题者刻意给出了“当小球受到垂直纸面方向的扰动做微小摆动时，等效于悬挂点位于小球重垂线与 交点的单摆”这一条件。由于该条件的给出，此题A、B选项的解答过程可规避对细绳及小球的运动学分析。笔者与某校2025届高三头部班级的物理教师协调后，将此题选人其所在班级周测卷进行实测，最终得分率在 8 8 % 左右（图2）。然而，因为题目中这一明确告知替代学生完成了物理建模步骤，这也使得一部分学生在完成本题后进行错误归纳时，忽略了其适用条件—“滑轮”模型，部分教师在模仿本题命制此类试题时也因此产生了错误（如浙江省新阵地教育联盟2025届高三上学期第一次联考第10题）。究其原因，是一部分学生和教师未对这一近似条件的近似合理性进行深入探究、分析释疑，未明晰其内涵。

由于高考试题常常作为各类练习题设计的重要参考和学习基础，对于题目背景及其内涵的不准确理解必定会不可避免地影响高考题在教学中的作用，且不利于学生形成准确的物理概念和全面的物理认知。因此，对于这一类椭圆摆微振动的近似合理性问题及其内涵进行探究，通过有效手段明晰难题内涵是非常必要的。

3 试题分析建模

3.1 通用模型建模

设任意时刻小球所在位置为 P 点 ， A B 中点为原点 o ，斜杆的倾角为 θ ，细绳长为 2 l 。结合本题中小球被细线穿过并悬挂这一特点，可知 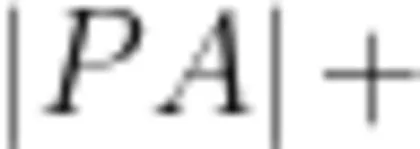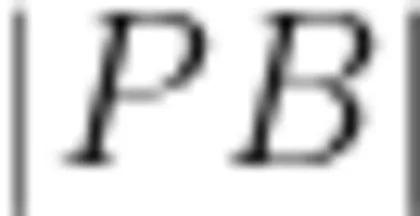为一定值，同时根据二次曲面相关数学知识，P 点一定在一个以 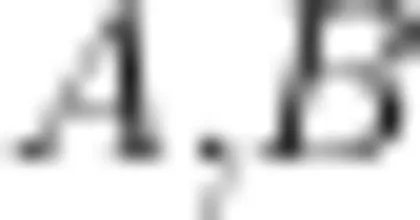两点为焦点、焦距为 2 d = 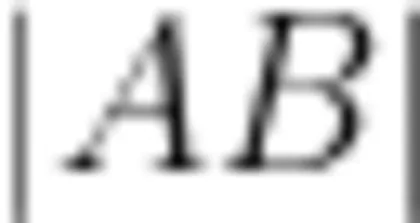构成的一个倾斜的椭球面上。在通用模型建模的过程中，和高考原题有所不同的是，笔者不指定小球所受微扰动的具体方向（即微扰动的方向任意）。

以 x 轴为转轴转动坐标架，将 O x y z 坐标系变换为OXYZ坐标系，使得坐标轴 Y 完全落在斜杆 所在直线上。在 o X Y Z 坐标系中，设该倾斜的椭球面方程为

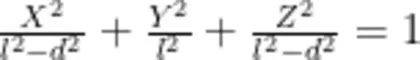
考虑转动过程，由线性代数的知识可得，由o x y z 坐标系变换为 o X Y Z 坐标系所利用的旋转矩阵 R 为[3]

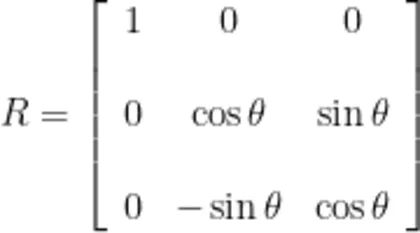
从而可得两个坐标系下各维度坐标的变换关系为

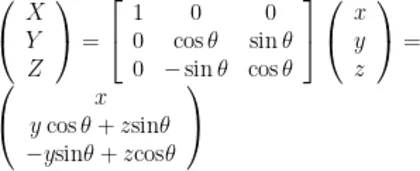
代人原方程，可得在 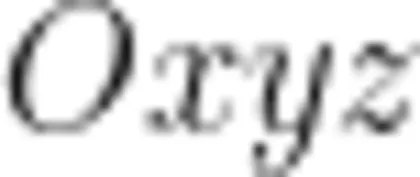坐标系中，该倾斜的椭球面方程为

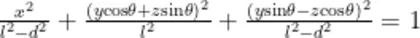
令 x = 0 ，可得到在微扰动下小球在纸面上振动所属曲线的方程。其中，平衡位置当且仅当在 z 取到最小值时取得，也即此时该二次方程对于 y 的判别式为0，得到平衡位置的坐标 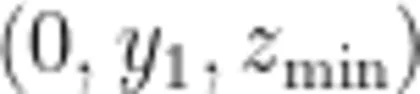后，便可以计算得到此处曲率圆的曲率半径

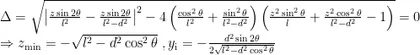
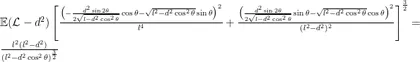
将 代人 o x y z 椭球面方程表达式中，得到在微扰动下小球在垂直于纸面方向进行振动的轨迹所属曲线的方程（即振动轨迹只是该方程

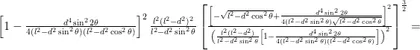
3.2用Mathematica软件探究微扰动下小球在纸面和垂直纸面方向上的振动轨迹

无论是在垂直纸面方向还是在纸面上，微扰动下，小球的振动轨迹都十分复杂多变。对于倾角 θ 不同的斜杆，其轨迹也不相同，其中也蕴含着一些相似性。笔者利用Mathematica软件，对这些轨迹所属的曲线方程进行可视化。为了兼顾图像的展现力和代表性，笔者在可视化的过程中取倾角0=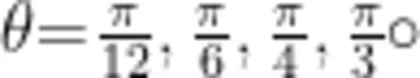

打开Mathematica软件，新建笔记本，对纸面上的振动轨迹所属的曲线方程进行可视化，输入如下命令：

1=3*1.5/Sqrt[3]

d=1.5 x=0

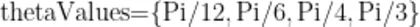
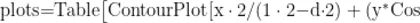
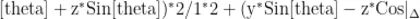
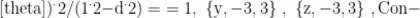（204 tourStyle - >

其中，Table表示对参量一定方式进行枚举，ContourPlot表示绘制隐函数图（等高线图），theta，thetaValues表示参量枚举的范围，这里表示的枚举集合为thetaValues，即为 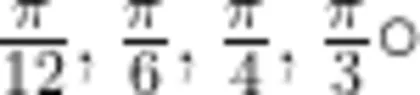如果要研究更多的角度值，则将向thetaValues集合中加入那些更多的角度值即可。随后，选中相应命令行内容，选择“计算单元”，即可作出微扰动下小球在纸面上的振动轨迹所属曲线的图像。通过Show 函数，笔者将 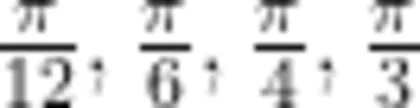种情况下作出的图像合并在一张图中，如图3所示。

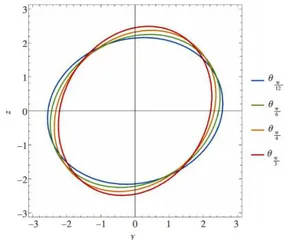
（右侧各图例从上到下与左侧各振动轨迹所属曲线沿 z 轴正方向从内到外一一对应）