对“等时圆”模型的反向建模注重对结论的反向探究

中图分类号：G633.7 文献标识码：A文章编号：1003-6148（2025）4-0065-3

《普通高中物理课程标准（2017年版）》指出，学生应达到的目标有“具有建构模型的意识和能力；能运用科学的思维方法，从定性和定量两个方面对相关问题进行科学推理、找出规律、形成结论。"在以往的教学中，注重的是在教师的指导下，让学生对已有的模型进行分析，学会拆模、析模，运用规律和方法解题，而没有关注学生发现问题、建构模型的能力。根据实际情境建立模型是当前考试评价的重要方面，也是物理学科关键能力之一，因此教学的重心要前移，要注重引导学生建构模型，培养模型建构的能力。通过对结论的思考，反向建立模型，也是一种重要的建模能力培养方式。

1 光滑轨道的“等时圆”模型

在高中必修一“运动和力的关系”章节教学后，在牛顿第二定律和运动学结合的习题教学中，会涉及到一个基础模型一“等时圆”，往往教学的过程是直接给出了“等时圆”的模型，让学生去解决问题，然后再用相应的习题来拓展“等时圆”的应用。

模型如图1所示，光滑圆轨道竖直放置，半径为 R ，圆心为 o ，最低点为 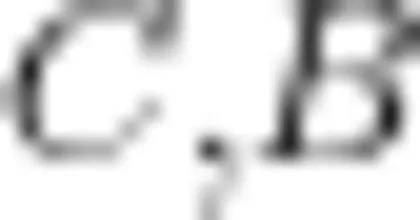为圆上任意一点。一物块（可看成质点）从 A 处静止开始下滑，试证明沿不同角度轨道下滑到圆周上的时间是定值。

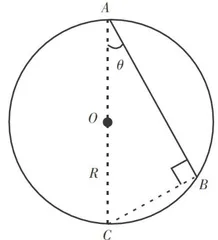
证明连接 和 B C ，可知 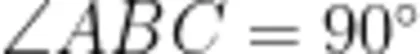，设∠ C A B = 6 ，则 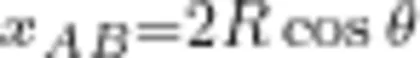，物块下滑的加速度为a=gcosθ，由运动学公式可知 xAB=at²，解得t= 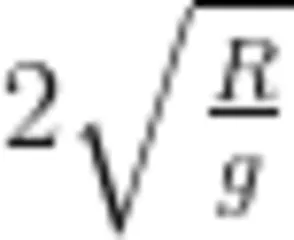。根据最终 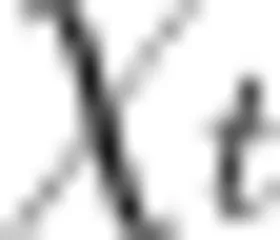的表达式可知，下滑时间 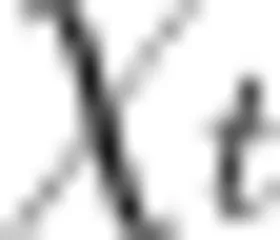与倾角 θ 无关，即从 A 点滑到圆周上任意一点的时间都相同。还可以推知，物块从 A 点自由落至c 点从 B 点由静止开始滑到 C 点所用的时间是相同的。

这个知识点解决的过程是通过给定的模型，让学生运用学过的规律来解决提出的问题，虽然能够让学生记住这个模型，但对于这个“等时圆”是如何建构出来的，并没有进行相应的铺垫，使这个“圆”出现得非常突兀，没有进一步培养学生建构模型的能力。

2 “等时圆"模型的反向建构过程

2.1 最基础的斜面下滑问题

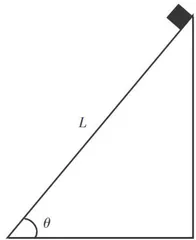
如图2所示，一个光滑的固定斜面长度为L ，倾角为 θ ，一物块（可视为质点）从斜面顶端静止下滑，求物块滑到底端的时间。

解答 物块沿斜面下滑的加速度为 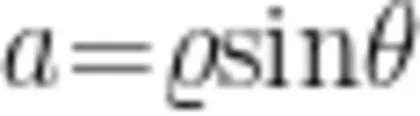根据运动学公式 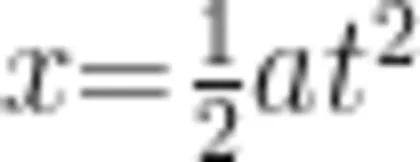，代人 L 和 进行计算，可得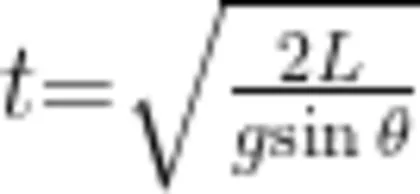

这个解题过程非常简单，从物理意义上来理解，就是求解初速度为0、以 a=℘ s i nθ 的加速度通过了 L 的路程的时间。若将这个结果与自由落体的时间表达式 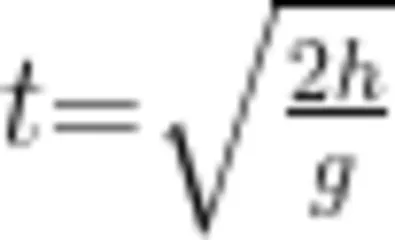2h对比，此表达式是不是可以等效理解为物体以大小为 a = g 的加速度、通过了h= 的位移自由下落所用的时间呢？

2.2 从斜面到自由落体的反向建模

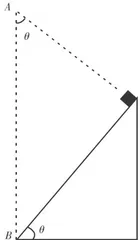
根据上题的思路，如何根据结论去建构一个相应的与斜面模型相关的自由落体模型呢？这涉及到如何在这个斜面模型上找到一个包含 L 和θ 的结构。既然是自由落体，那么我们可以建构下落到最低点的自由落体运动。对于如何找到θ ，根据数学知识，可以过斜面最高点作斜面的垂线，如图3所示。从建构出来的从 A 至 B 的自由落体运动来看，AB的长度为L 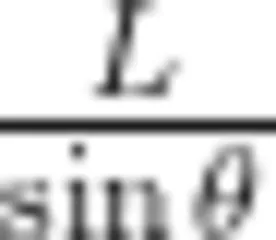。，可以较容易地判断出沿斜面下滑的时间和自由落体的时间是相同的。

2.3 结合斜面及自由落体的“等时圆"的建构

根据图3，再进行深入思考，由于 θ 是任意取的，那么以 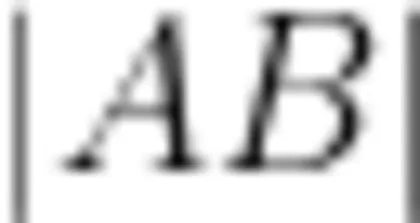为斜边构成的直角三角形中，物体以零初速度沿着连接 B 点的弦构成的光滑斜面下滑的时间都应当与从 A 点开始至 B 点的自由落体时间是相等的。如图4所示，可以发现，这些轨道虽然倾角和长度都不一样，但根据几何原理，这些斜面的顶点都是在以 为直径的一个圆上。将这些点连起来，考虑到左右对称，则是一个完整的圆。如果考虑到三维空间，则是一个以A B 为直径的球面。可得到结论：以 A B 为直径的圆（球面）上，从任意一点连接最低点建构一个光滑斜面，物体以零初速度下滑到最低点的时间均相同。

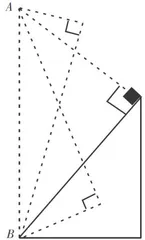
如果要得到图1所示的“等时圆”，只需要根据对称性进行平移即可。因此，最终模型的结论应当是，光滑情况下，物体从顶点由静止开始沿弦滑到球面上任意点（或者从球面上一点沿弦滑到最低点）的时间均是相同的。

3 同类型模型的建构

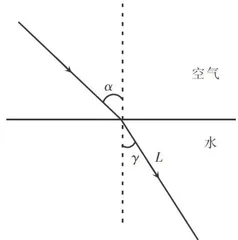
如图5所示，一束光自空气以入射角 α 斜射入水中，折射角为 γ ，在光进入水后经过 L 的距离需要的时间是多少？（已知光速为 ∣ c ∣ ）

解答本题比较简单，折射率 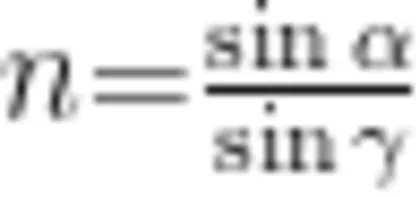sina，光在水中的速度为 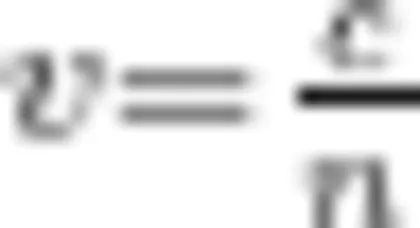，然后只需要用公式 x = v t ，就可以直接得出答案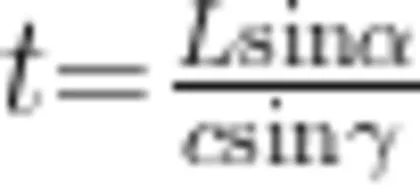

但是，不同色光对同种介质的折射率是不一样的，故以相同的人射角进入水中之后的折射角的大小是不同的，光速也是不同的。那么，一束复色光折射入介质中，经过相同的时间，不同色光都到达怎样的位置呢？

设sinα和 是定值，那么时间的确定与 L 和siny有关。有了基础“等时圆"的建构，是不是也能同样寻找一个定值来代替呢？可以引导学生进行图6所示的模型建构。

XAcsinα，所以可知不同色光到达圆弧ABC上的时间都是相同的。

其中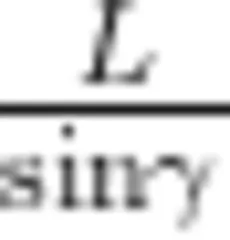， 就是图中的直径 A C ，两者的比值是定值。对于不同色光，虽然折射角 γ 和水中的光速是不一样的，经历相同的时间经过的距离也不一样，但根据 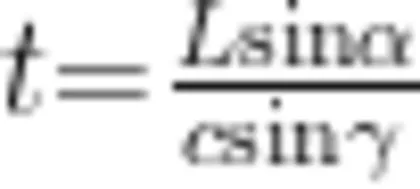进行代换得到 t =

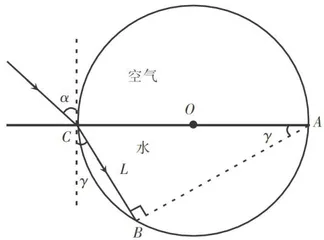
这是一个光学上的“等时圆”。两个不同的“等时圆”，解决问题的本质是相同的，整体反向建模的方法和思维的过程是异曲同工的。可见，只有在引导学生建模的过程中，注重模型的生成，才能有效地培养学生的学科关键能力。

4小结

高中物理的许多二级结论，都是在简单模型的重构中生成的，比如平抛速度的反向延长线过位移的中点等。从以上分析可以看到，通过引导学生对结论中表达式的进一步分析，自主进行建模，在物理学科关键能力培养上远比直接给学生模型更有效。通过引导学生分析建模，在教学中不是“授之以鱼”，而是“授之以渔”，对学生探究能力的培养有很大的帮助。

参考文献：

[1]王进峰.“等时圆”的一般规律[J].物理教学，2022，44（4）：52-53.

[2]卞志荣.构建“等时圆”模型速解相关题[J].物理教学探讨，2007，25（6）：24-25.

[3]田川.对等时圆问题的探讨[J].物理教学探讨，2019，37（5）：59-62.

（栏目编辑 蒋小平）