关于金属线圈会不会“卡”在磁场边界的思考

中图分类号：G633.7 文献标识码：A

在中学物理中有这样的一类问题，就是研究金属线圈经过磁场区域时仅在安培力的作用下金属线圈的运动学规律以及动力学表现[1。由于金属线圈在运动过程中受到的安培力与金属线圈运动的速度有关，而安培力又反过来影响金属线圈的运动速度，故金属线圈在做一个加速度减小的减速运动，这种减速运动仿佛是金属线圈受到了一个摩擦阻力一样，故称为电磁阻尼运动。虽然中学阶段不会去具体地研究金属线圈的运动学方程，且可以用一些守恒定律或者是运动变化过程中的平均量或者平均思想来思考和解决问题，但是这些平均量是否能起到等效的作用值得深思[2-3]。接下来，将利用微积分的方法研究正方形金属线圈在无摩擦情况下进出足够大匀强磁场时的运动学方程[4]。

1高中最经典的正方形金属线圈通过匀强磁场问题

例题如图1所示，在光滑的水平地面上有一正方形金属线圈以初速度 向右运动，在其前方有一垂直纸面向里的正方形区域匀强磁场，文章编号：1003-6148（2025）4-0070-3磁场区域足够大。已知金属线圈完全进入磁场后的速度刚好减半，则金属线圈从进入磁场到完全离开磁场的整个过程中速度随时间的变化可能正确的是（ ）

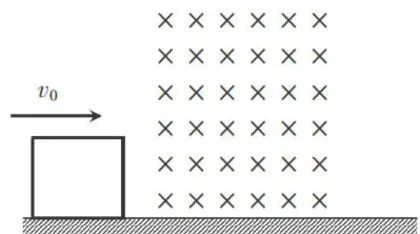
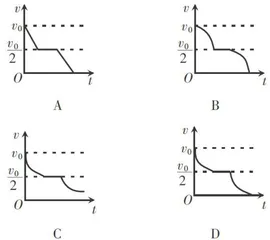
小的减速运动，不足以判断出正确选项。相比于得出正确选项，我们会更想知道：金属线圈到底做怎样的运动，线圈会不会“卡”在磁场边界进不来，或者出不去，金属线圈的运动学方程到底是怎样的。下面从牛顿第二定律出发来研究这个运动过程。

2 正方形金属线圈进入匀强磁场时的运动学方程

想要搞清楚正方形金属线圈会不会被“卡”在磁场边界，最直接的方式就是求出正方形金属线圈进出匀强磁场时的运动学方程。金属线圈进入匀强磁场时，在不考虑摩擦力的情况下水平方向仅受安培力作用，当正方形金属线圈的运动速度为 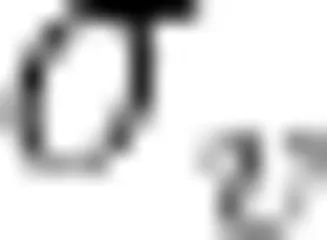时，由牛顿第二定律可得

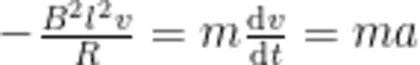
其中， m 为正方形金属线圈的质量，l为正方形金属线圈的边长， R 为正方形金属线圈的电阻， B 为匀强磁场的磁感应强度，且规定运动方向为正方向。（1）式可变为

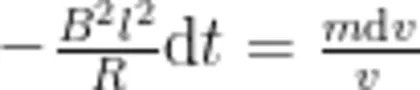
根据动量定理也可直接得出（2）式，（2）式正是该运动过程中动量定理的微分形式。想要知道正方形金属线圈的运动学方程，只需（2）式两边同时对正方形金属线圈进入匀强磁场过程进行积分即可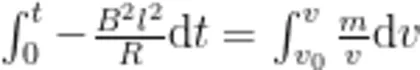， mdu，计算后得到

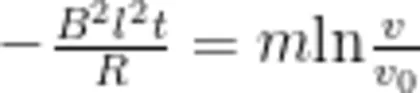
其中， 为正方形金属线圈速度从 变成 v 的时间。由（3）式可以得到正方形金属线圈进入匀强磁场时的速度一时间关系

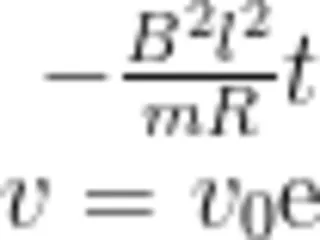
（4）式说明正方形金属线圈在进入匀强磁场过程中速度呈指数衰减，且速度衰减的快慢程度由因子T=B 决定。从（4）式可以看出，正方形金属线圈的质量和电阻越大，速度衰减得越慢，正方形金属线圈边长和匀强磁场磁感应强度越大，则速度衰减得越快，这也是电磁阻尼的原理，符合我们的预期。将（4）式两边同时对时间积分

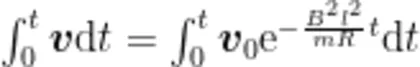
得到正方形金属线圈进入匀强磁场时的位移大小和时间的关系

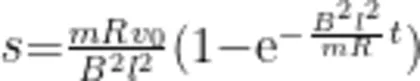
有了（5）式就可以分析正方形金属线圈进出匀强磁场时会不会“卡"在磁场边界的问题

3正方形金属线圈能否完全进入或完全离开磁场的条件

正方形金属线圈进入磁场的过程是一个消耗线圈动能的过程[5-6]，若正方形金属线圈较长，就有可能无法整体进出磁场，被“卡”在磁场边界。由（5）式可知，在磁场区域足够大的情况下，正方形金属线圈能运动的最大位移

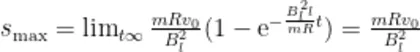
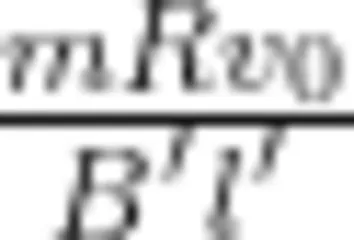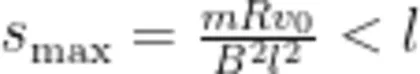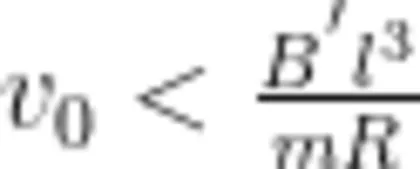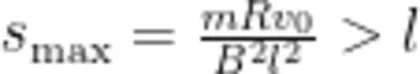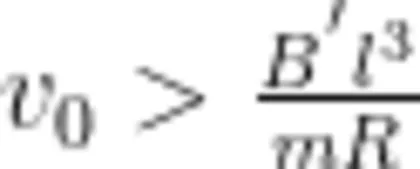由（6）式可知，所谓“磁场区域足够大"并不是无穷大，只需磁场宽度不小于 即可，且由（6）式可得正方形金属线圈能完全进入磁场的条件：若 ，即 则正方形金属线圈被"卡"在进磁场的边界;若 ，即 则正方形金属线圈可以整体进入磁场；若 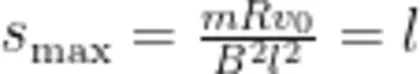mRvo=l，即vo 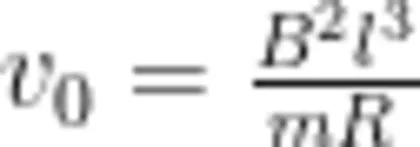则正方形金属线圈刚好能整体进入磁场边界。

接下来一个自然的问题是，若正方形金属线圈被“卡"住，则卡在什么位置；若正方形金属线圈能整体进入磁场，那么能否整体冲出磁场边界（不难理解，正方形金属线圈出磁场时的规律跟进磁场时的规律是一样的，只不过出磁场时的初速度变为整体进入磁场时的末速度）。通过（2）式可以得到正方形金属线圈整体进入磁场后的末速度。由（2）式得

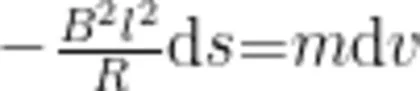
其中， ds = v dt ，是正方形金属线圈在此时间内的位移，由（7）式两边同时对变量积分 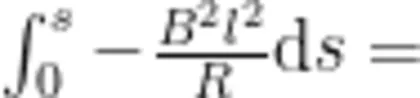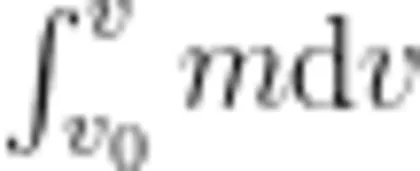得到

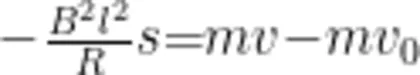
其中， s 为正方形金属线圈从速度 变为 所发生的位移大小，由（8）式可得正方形金属线圈完全进人磁场后的速度

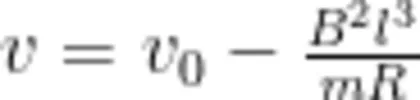
有了正方形金属线圈完全进入磁场后的末速度，同理可得正方形金属线圈能完全出磁场的条件：

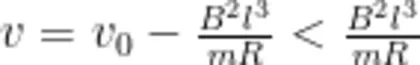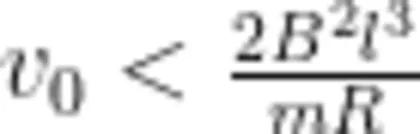若 即 则正方形金属线圈被"卡"在出磁场的边界；

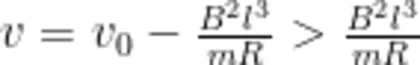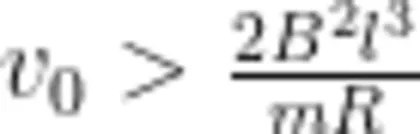若 即 则正方形金属线圈可以整体出磁场边界；

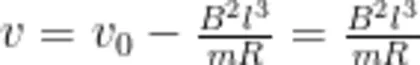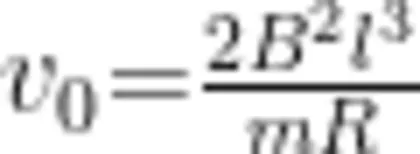若 即 则正方形金属线圈刚好可以整体出磁场边界。

此例中已知正方形金属线圈完全进入磁场后的速度为 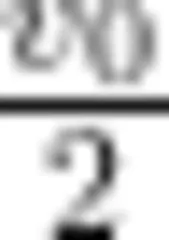，故正方形金属线圈刚好可以整体出磁场边界，即出磁场后的速度为零，D选项正确。另外，如果正方形金属线圈被“卡"住，只需令（8）式中的末速度 v = 0 ，即可得正方形金属线圈进入磁场的长度 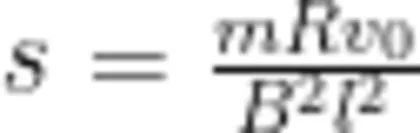，此时 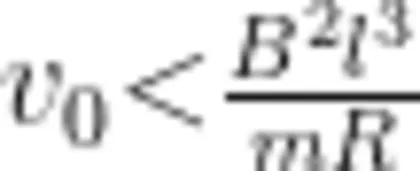，故s 的位置。

参考文献：

[1]许倩，徐平川，黎国胜.电磁感应中速度随位移均匀变化的“另类匀变速直线运动”的深入研究[J].物理教学，2022，44（9）：8-11.

[2]钟祺浩.从一道高考题谈能量守恒思想[J].物理教师，2024，45（8）：58-60.

[3]王朝辉，于正荣.由一道电磁感应问题谈物理量的平均值[J].物理教师，2023，44（8）：56-57，60.

[4]陈恋.高中物理解题中微元法的应用[J].广西物理，2024，45（1）：103-105.

[5]李卫松.电磁感应现象中的力和能量转换之间的关系[J].物理教学，2024，46（1）：16-18，28.

[6]娄国华.例析电磁感应中的能量问题[J].广西物理，2023，44（1）：208-210.

（栏目编辑 蒋小平）