匀强电场的边缘电场总可忽略吗

中图分类号：G633.7 文献标识码：A文章编号：1003-6148（2025）4-0073-4

各点的电场强度大小相等、方向相同的电场叫匀强电场。相互靠近且正对的、带等量异种电荷的平行金属板的电场中，中央部分的电场可以看作匀强电场；匀强电场的周围存在着非匀强电场，将其称作匀强电场的边缘电场，简称边缘电场[1]。在涉及匀强电场的很多问题中，为了使问题简化，往往都忽略了边缘电场。那么，在各种具体问题中，边缘电场是否都可以忽略呢？

1 平行板电容器的电容

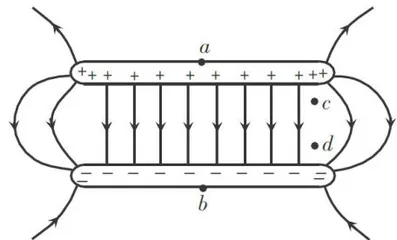
平行板电容器由一对平行、正对的金属板组成，板间距离远小于板的大小。带电平行板电容器的电场如图1所示。如果忽略边缘电场，即认为电荷在极板上的分布和电场线在空间的分布是均匀的（图2），那么由高斯定理容易求得场强

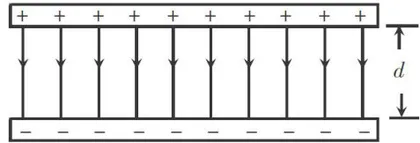
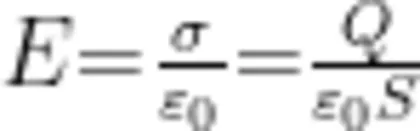
式中， σ 是面电荷密度，即单位面积所带的电荷量， Q 是极板上的电荷量， s 是极板面积。两板间的电压

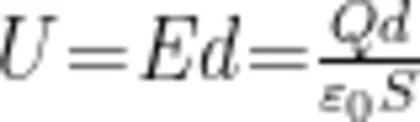
式中， d 是极板间距离。电容器的电容

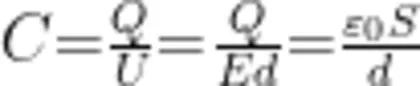
这就是平行板电容器的电容公式。

由于同一极板上的电荷之间相互排斥，极板边缘的电荷较为密集，电容器中电荷和电场线的真实分布情况如图1所示。极板中央部分用于产生匀强电场的电荷 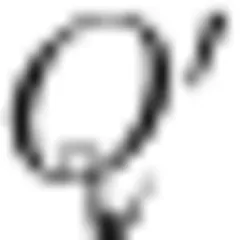小于极板上的总电荷 Q 两极板间的真实电压

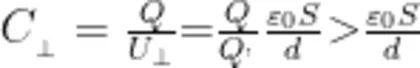
可见，由于存在边缘电场，平行板电容器的电容公式给出的电容值小于真实值。那么，这种差异在极板间距离远小于极板大小的情况下是否可以忽略呢？

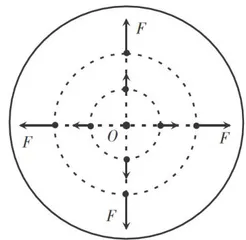
为讨论方便，假设极板是圆形的。由对称性知道，圆形极板带电后，在同一圆周上的各点，面电荷密度 σ 相同。如果极板的半径 R 较小，那么除了圆心 o 处的电荷受到四周电荷对它的作用力的合力等于0，其他点的电荷受到以它到 o 的连线为半径的圆内的电荷作用力的合力均沿半径向外，且离 o 越远的电荷所受的合力越大，如图3所示。于是，离 o 越远的点， σ 越大。如果 R 较大，那么 o 点附近的任何电荷，周围电荷对它的作用力的合力为0，远处电荷对它的作用力可以忽略。这样，在以 o 为圆心、半径较小的一个圆内， σ 可以看作处处相等，外围环上的 σ 较圆内大，且离 o 越远处 σ 越大。

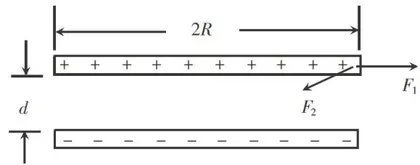
上面只考虑了同一极板上电荷之间的斥力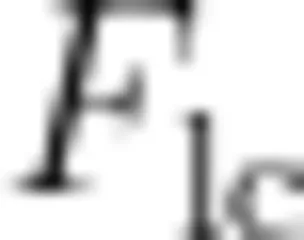 。事实上，极板边缘上的电荷还受到另一极板的吸引力 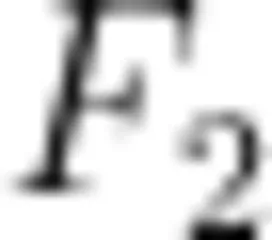，如图4所示。在 d 不变 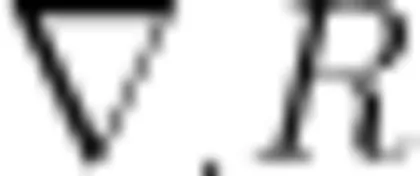趋向于 ∞ 的情况下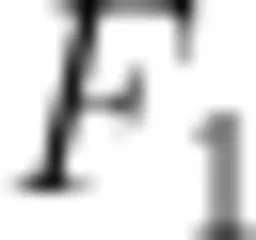， 和 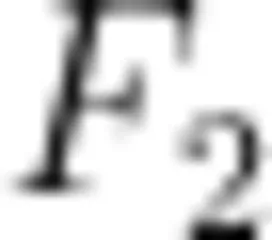将趋向于大小相等、方向相反。在这种情况下，极板边缘部分与中央部分的 σ 将趋向于相等。

根据上面的分析，可以将圆形极板上的电荷分布简化为图5所示的模型：在半径为 R-Δ R 的圆内，电荷均匀分布，面电荷密度为 σ ，在宽度为Δ R 的环上，平均面电荷密度 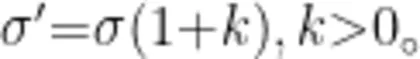当d 不变且 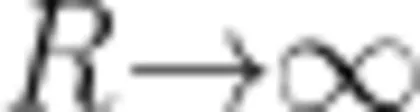时 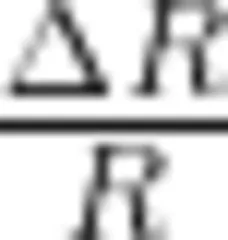和樂 k 均趋于 0

要考虑边缘电场时，平行板电容器可以看作是两个电容器的并联，一个是两个圆面正对的电容器，另一个是两个环面正对的电容器。前者的电容

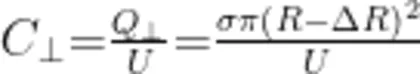
后者的电容

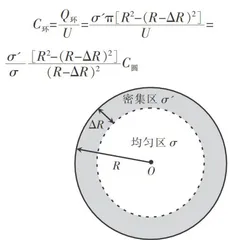
另一方面，因两个圆面之间的电场是匀强的，因此有

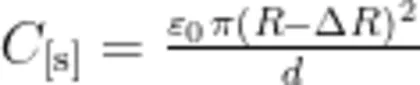
平行板电容器的真实电容

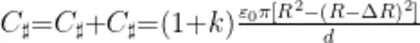
化简并忽略 Δ R 的二次项，得到

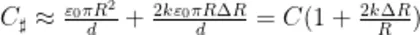
其中，C=εTR² 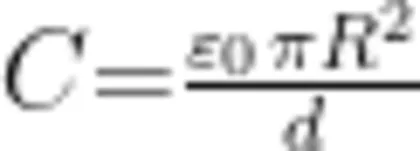在 d 不变 ∇⋅ R 趋向于 ∞ 时，△R/R和 k 趋于0，有

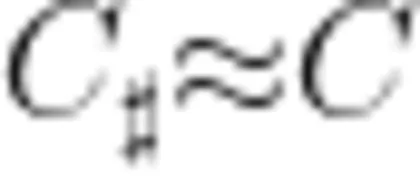
可见，对于平行板电容器的电容，在板间距离远小于极板大小的条件下，边缘电场可以忽略。

2 带电粒子在电场中的偏转

如图6所示，带电粒子以一定的初速度射入带等量异种电荷的平行金属板产生的电场，最后打在接收屏上。在计算粒子打在屏上什么位置时，通常都是忽略边缘电场的。那么，它真的可以忽略吗？

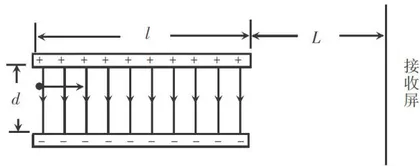
设两块金属板是边长为 l 的正方形，板间距离为 d ，所带的电荷量分别是 + Q 和-Q。在 d < < l 时，两板正对区域的场强

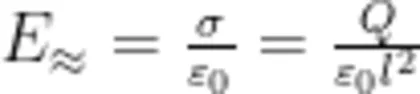
要计算边缘电场的场强是很困难的，下面作简化估算。设想把每块极板上的电荷都集中到中点，这对带等量异种电荷的金属板就成为一个电偶极子，如图7所示。

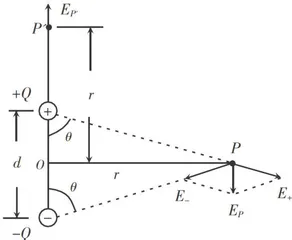
位于两电荷连线的垂直平分线上距连线中点 o 为 r 的 P 点，两电荷在该点产生的场强

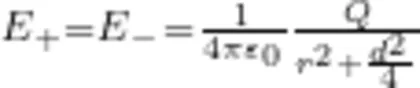
电偶极子在 P 点产生的场强

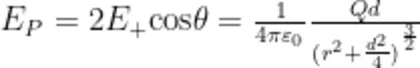
在 r>>d 的条件下，得到

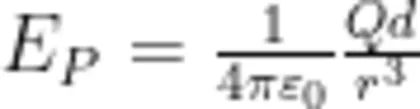
同样，可以求得两电荷连线上到 o 点的距离 r>>d 的 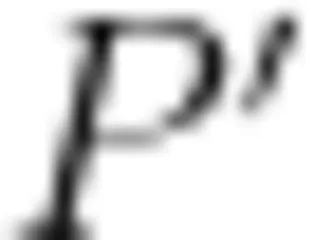点的场强。

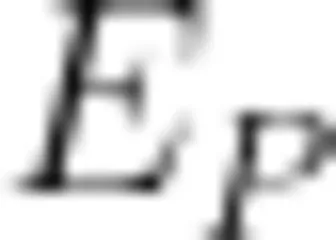虽然 和 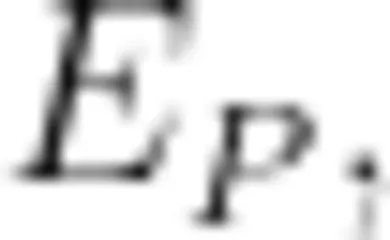不相等，但它们都与 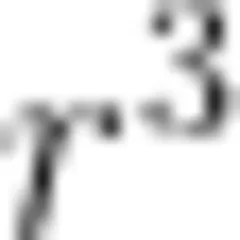成反比。可以理解为，电偶极子电场中的其他点，只要r>>d ，场强 E 也与 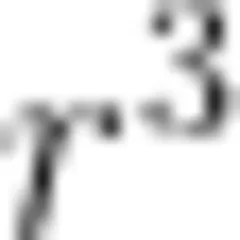成反比。

在 d < < l 的情况下，图6中匀强电场右侧边缘电场中的各点均满足 r>>d ，因此可以利用上面从电偶极子得出的结论，即边缘电场的场强与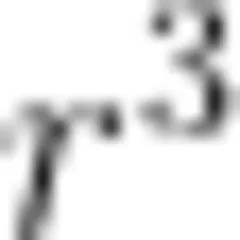 成反比。匀强电场右边缘处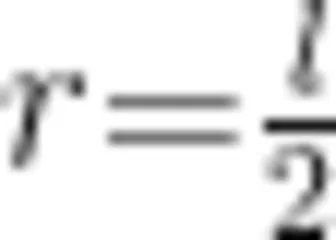， ，我们不妨设场强 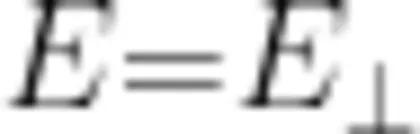（实际上是小于），与中心点 o 相距 r = l 的点，场强 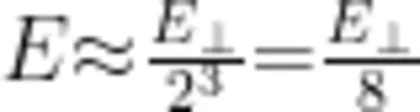，与0相距 的点，场强 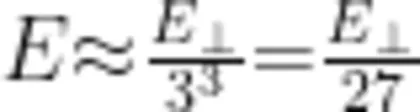可见，边缘电场的场强远小于匀强电场的场强，带电粒子在边缘电场中受到的电场力也远小于在匀强电场中受到的电场力。因此，在 d < < l 的情况下，对于带电粒子在电场中偏转的问题，可以忽略边缘电场。